Величина и направление электромагнитной силы в случае одного контура с током

Электромагнитные взаимодействия в асинхронном двигателе.

При совершенной справедливости формулировки, говорящей о стремлении всякого контура с током охватить наибольший внеш­ний поток, интересно отметить, что в некоторых практических случаях это стремление, по существу явления, не может быть полностью удовлетворено. Классическим примером этого рода служит возникновение вращающего момента в асинхронном двига­теле. Здесь электромагнитное взаимодействие имеет место между вращающимся полем статора и токами, индуктируемыми этим полем в обмотке (или теле) ротора. Для того, чтобы поле статора могло индуктировать ток в обмотке ротора, необходимо, чтобы проводники последней пересекались линиями вращающегося поля, что, очевидно, может иметь место только в том случае, если ротор вращается медленнее, чем поле статора, т. е. если имеет место так называемое скольжение. При наличии такого скольжения, т. е. при наличии индуктированного тока в каждом контуре обмотки ротора, этот контур стремится охватить наибольший внешний поток,— в данном случае наибольшее число магнитных линий вращающегося поля. В результате ротор двигателя вращается, стремясь „догнать" вращающееся поле, т. е. получить ту же скорость вращения. Но как только такая, так называемая синхронная, скорость будет до­стигнута, что мыслимо лишь в идеальном случае отсутствия всяких механических сопротивлений, тотчас же прекратится пересечение полем статора обмотки ротора, т. е. прекратится всякое электро­магнитное взаимодействие между обмотками ротора и статора, Таким образом, осуществление стремления к охвату наибольшего

потокаприводит к исчезновению самой причины этого „стре­мления"— электромагнитной силы. По мере увеличения охватываемого потока, по мере приближения к моменту наибольшего охвата, эта сила уменьшается, ассимптотически приближаясь к нулю. Это, конечно, вполне естественно, так как в рассматриваемом предель­ном идеальном случае „стремление" будет удовлетворено. Практи­чески же, благодаря наличию механических сопротивлений, ротор асинхронного двигателя никогда не может „догнать" вращающееся поле, т. е. контуры его обмотки никогда не могут охватить, на­ибольшего возможного потока.

Рассмотрев физическую природу явления возникновения дви­жений в электродинамической системе, обратимся к определению величины и направления электромагнитной силы в различных ча­стных случаях.

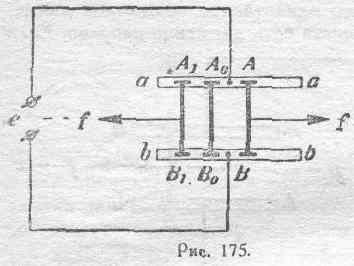
Напомним еще раз основное выражение (72), определяющее электромагнитную силу:

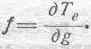
Для составления этого выражения, т.е. для определения вели­чины и знака электромагнитной силы, необходимо прежде всего составить выражение для электрокинетической энергии.

В общем случае:

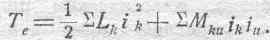
В частных случаях систем, состоящих из немногих контуров, выражение Т_е значительно проще.

Сделаем здесь прежде всего одно общее замечание относительно направления электромагнитной силы. Из выражений для электро­кинетической энергии и, следовательно, электромагнитной силы, непосредственно следует, что направление последней не изменится, если направления токов во всех составляющих систему контурах изменить на обратные: все члены выражения Т_е второй степени относительно сил токов; таковы же, очевидно, и члены выражения/, так как последнее получается из первого посредством частного дифференцирования по геометрической координате. Примером, иллю­стрирующим это положение, может служить двигатель постоян­ного тока: при одновременном изменении направления тока как в якоре, так и в обмотке возбуждения двигателя, направление его вращения останется неизменным.

Обратимся к первому из рассмотренных выше случаев, именно к силам, действующим на уединенный контур с током, находящийся

в своем собственном магнитном поле. Электрокинетическая энергия такого контура выражается так:

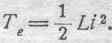
В данном случае электромагнитная сила представится в сле­дующем виде:

иными словами, положительное направление электромагнитной силы соответствует движению в таком направлении, в котором коэффи­циент самоиндукции контура увеличивается. В случае плоского кольцеобразного контура (рис. 172), одним из возможных напра­влений движения, при котором будет иметь место изменение коэффициента самоиндукции, является на­правление радиуса кольца r.

Таким образом, в этом случае:

т. е. будет иметь место равномерное давление по окружности кольца, напра­вленное изнутри наружу в сторону внешней нормали. При этом следует обратить внимание на то обстоятель­ство, что сила в рассматриваемом слу­чае кругового контура есть некоторая

„обобщенная сила″ — полное давление на контур изнутри наружу. Механическую силу, отнесенную к единице длины контура, мы по­лучим, разделив f на длину этого контура, т.е.

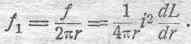
Выведем еще выражение для работы, совершаемое силою / в случае эластичного контура. Из соотношения (124) получаем элементарную работу:

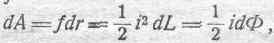
т. е. элементарная работа полной электромагнитной силы равна в данном случае (одной цепи) половине произведения силы тока на приращение потока. Интересно отметить строение последнего выражения: ¹/₂ i есть не что иное, как энергия, отнесенная к одной магнитной линии (§ 21), dФ — приращение числа магнитных линий, пронизывающих контур. Таким образом, выражение ¹/₂ idФ совер­шенно отчетливо выражает приращение электрокинетической энер­гии данного контура, как приращение энергии магнитного потока самоиндукции.

В случае проводящего контура, изображенного на рисунке 172, имеет место проявление еще и другой электромагнитной силы, обусловленной тем обстоятельством, что коэффициент самоиндук­ции контура при сохранении его среднего диаметра может увели­чиваться в связи с уменьшением толщины провода, из которого состоит контур. Принимая в этом случае за независимую коорди­нату объем провода v, на основании уравнения (123) можем написать:

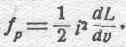
Так как очевидно, что:

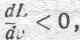
то сила f_p отрицательна в отношении внешней нормали к поверх­ности провода. Другими словами, эффект силы f_p состоит в поя­влении давления на эту поверхность в направлении снаружи внутрь. Следовательно, сила f_p стремится уменьшить объем провода, т. е. его диаметр. Это именно и наблюдается на практике в индукцион­ных электрических печах, в которых сильный ток идет по распла­вленному металлу, налитому в кольцевой желоб. В результате возникающих со стороны потока самоиндукции сильных давлений на поверхность металла иногда происходит в некотором месте сжатие жидкого проводника, доходящее до предела, т. е. до раз­рыва цепи. К. Геринг назвал это явление пинчэффектом:

В рассмотренном выше примере увеличения коэффициента само­индукции контура под действием растягивающей контур (см. рис. 172) электромагнитной силы, это увеличение сопровождается увеличе­нием площади контура. То же самое имеет место, как указано было раньше, в случае всякого контура, кривизна которого одного знака во всех частях. Поэтому экспериментальная иллю­страция действия электромагнитной силы в случае единственного контура проще всего осуществляется именно на контурах одного знака кривизны, где характер наблюдаемого изменения площади, охватываемой контуром, вполне соответствует характеру измене­ния коэффициента самоиндукции. Классическим опытом этого рода является известный опыт Ампера, состоящий в следующем.

Два заполненных ртутью корытца аа и bb включаются в цепь и соединяются проводящим мостиком АВ, плавающим по ртути, как показано на рисунке 173.

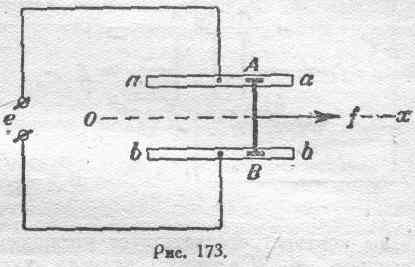
При включении тока мостик под действием электромагнитной силы f движется вправо, что приводит к увеличению охватываемой контуром площади. Такое направление электромагнитной силы вполне соответствует, как это видно из конфигурации контура, увеличению его коэффициента самоиндукции. Предполагая в данном случае весь контур жестким, и подвижной— только часть АВ, мы должны при вычислении электромагнитной

силы воспользоваться геометрической координатой в соответствии с наличной степенью свободы движения, т. е. перемещением, парал­лельным направляющим мостика. Обозначая эту координату через х к считая X положительным в направлении от 0 к х, имеем для величины электромагнитной силы в данном случае:

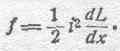
Не следует, однако, думать, что единственно возможное движе­ние мостика в рассматриваемом опыте есть движение направо. Если за исходное положение мостика принять поло­жение А'В' (рис. 174), то конфигурация кон­тура тока, которая полу­чится при таком исход­ном положении мостика, не дает нам права утвер­ждать, что увеличение коэффициента самоин­дукции L будет соответ­ствовать увеличению охватываемой контуром площади.

Детальное рассмотрение физической картины явления и теоретический анализ показывают, в этом случае, когда кривизна контура не везде одного знака, что увеличение коэффициента самоиндукции L (вместе с тем, конечно, и увеличение охватываемого кон­туром потока, а также и электро­кинетической энергии контура) будет иметь место при движении - мостика налево, т. е. при явном уменьшении охватываемой конту­ром площади. Кажущаяся про­тиворечивость такого результата разъясняется на основе приведен­ного выше общего рассмотрения физической природы явления элек­тромагнитной силы. В частности для данного случая, можно сказать следующее: наибольшей плот­ностью (В) магнитный поток обладает в непосредственной близости к проводнику; следовательно, увеличение периметра контура, являю­щееся результатом движения мостика — в этом случае — налево может в случае достаточного удаления прочих частей цепи от корытец повлечь за собой увеличение связанного с контуром потока самоиндукции, которое с избытком компенсирует уменьше­ние потока, являющееся следствием уменьшения площади контура. Так как и при движении мостика направо, в случае рисунка 173, и при движении его налево, в случае рисунка 174, коэффициент

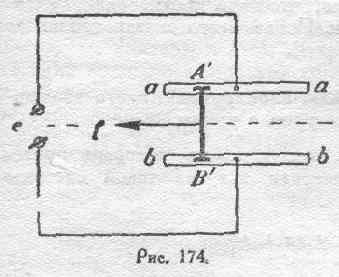
самоиндукции контура увеличивается, то можно найти некоторое среднее положение мостика A ₀ B ₀(рис. 175), при котором контур будет обладать наименьшим коэффициентом самоиндукции.

Если это положение мостика взять за исходное, то движение его в ту или другую сторону будет зависеть от случайного начального импульса.

Рассмотренный вариант опыта Ампера, дающий уменьшение площади контура (движение мостика налево, рис. 174), был впервые поставлен уже упомянутым выше американским инже­нером К. Герингом и привел его к ошибочному заключению о неправиль­ности и неуниверсальности закона движений в элек­тродинамической системе, сформулированного Макс­веллом. Именно, полагая, что увеличение коэффи­циента самоиндукции всегда (независимо от кривизны контура) соответствует увеличению площади, охватываемой контуром, К. Геринг, получив уменьшение площади в ре­зультате опыта, сделал неправильное заключение, что в некоторых частных случаях движений под влиянием электромагнитной силы, поток, связанный с контуром, а стало быть и коэффициент самоин­дукции контура, может уменьшаться, что явно противоречит клас­сическим законам электродинамики. После всего сказанного выше ясна ошибочность такого заключения.

^l) Подробный разбор утверждений, К. Геринга и описание опытов, выяс­няющих их ошибочность, заключаются в упомянутой выше статье Е. А. Чернышевой и Е. Я. Семичева (см. примечание к § 109).

¹) Pinch — по-английски означает „ущемление".

Дата добавления: 2014-11-29