Случай сверхпроводящнх контуров

Для иллюстрации только-что сказанного рассмотрим некоторые случаи, когда токи в системе не сохраняются постоянными. В этом отношении особенный интерес представляют случаи сверхпроводящих цепей, сопротивление которых равно нулю и токи в которых могут поддерживаться без посредства внешнего источника энергии. Остановимся сначала на простейшем случае одной сверхпроводящей цепи. В этом случае ток, однажды индуктированный в проводнике, должен существовать неопределенно долго, оставаясь неизменным по силе, если система неизменна. Таким образом, обратимся снова к контуру, представленному на рисунке 164, и предположим, что внешний источник энергии отсутствует и при этом сопротивление (омическое) контура равно нулю:

r =0.

Так как физическая природа явления остается той же самой (именно: явление бокового распора магнитных линий не может исчезнуть от того, что внешний источник отключен), то несомненно, что стремление к увеличению площади контура будет иметь место и в этом случае. Если контур не жесткий и возможно надлежащее его деформирование, то он растянется, и площадь, им охватываемая, увеличится. Следовательно, будет иметь место и увеличение коэф­фициента самоиндукции, зависящего, как известно, только от раз­меров и конфигурации цепи. Но магнитный поток, сцепляющийся с сверхпроводящим контуром, измениться не может: количество магнитных линий, пронизывающих контур, остается неизменным (см. § 28). Если же поток остается неизменным при увеличении коэффициента самоиндукции, то, следовательно, уменьшается сила тока, так как

Ф_s=Li

и

i=Ф_s/L.

В связи с этим уменьшается и электрокинетическая энергия, равная

¹/₂Li²=¹/₂Ф_si,

что очевидно и из общих соображений: при отсутствии источника энергии работа может совершаться только за счет собственного запаса энергии системы.

Остановимся еще на вопросе об электрокинетической энергии. Величина Т_е определяется, вообще говоря, двумя факторами: вели­чиной коэффициента самоиндукции (зависящей от геометрических координат) и силой тока. Как показывает рассмотрение физической картины явления, непосредственным и обязательным результатом действия электромагнитной силы в рассматриваемой системе, состо­ящей из одной сверхпроводящей цепи, является увеличение именно коэффициента самоиндукции. Это и представляет собою то реаль­ное изменение, которое необходимо имеет место в системе вслед­ствие действия электромагнитных сил и которое само по себе, объективно, может способствовать увеличению электрокинетической энергии, если отвлечься от других факторов, не зависящих непо­средственно от действия электромагнитных сил (в данном случае мы имеем в виду силу тока). Но для того, чтобы система могла увеличить свою электрокинетическую энергию, должен существо­вать какой-то источник, за счет которого это увеличение энергии могло бы иметь место. Создать энергию система сама по себе не может. Поэтому, при отсутствии внешнего генератора, увеличение электрокинетической энергии не может иметь места, хотя причины и характер возникающих в системе движений нисколько не меня­ются вследствие отключения источника энергии: именно, эти дви­жения остаются такими, какие соответствуют возможному увеличе­нию электрокинетической энергии в случае постоянства силы тока, поддерживаемого от постороннего источника энергии.

В случае двух или нескольких сверхпроводящих контуров сущ­ность явления остается в общем та же, что и в разобранном случае одного сверхпроводящего контура, только несколько усложняется.

В виде примера рассмотрим два сверхпроводящих контура, по которым идут одинаково направленные токи (см. рис. 165). Маг­нитный поток, сцепляющийся с каждым из контуров, остается по­стоянным, каким бы изменениям система ни подвергалась в отношении формы и расположения. Вследствие отсутствия внешнего источника энергии, в результате движения под действием электромагнитной силы должно произойти уменьшение электрокинетической энергии. Ради простоты допустим, что оба контура жесткие. В таком случае могут происходить только перемещения контуров друг относительно друга. В случае токов, одинаково направленных, будет, как известно,

происходить сближение цепей. При этом коэффициент взаимной индукции М будет возрастать. Так как в то же время алектрокинетическая энергия:

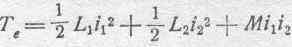
должна уменьшаться и вместе с тем мы в данном случае имеем:

L ₁=const, L ₂=const,

то очевидно, что должны уменьшиться силы токов i ₁ и i ₂. С целью дальнейшего упрощения описания происходящих явлений предпо­ложим, что контуры тождествены по форме, т. е.

L ₁ =L ₂,

и что

i ₁= i ₂.

Если контуры вначале были беспредельно удалены друг от друга, то мы имели

М= 0,

иэлектрокинетическая энергия системы могла быть представлена в форме:

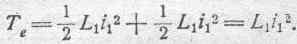
В случае сближения контуров до предела, мы получим (см. § 102)

M=L ₁ =L ₂.

В то же время обособленные ранее магнитные потоки каждого из контуров сольются теперь в один общий поток, сцепляющийся одновременно с обоими токами i '₁ и i '₂. При этих условиях полный поток, сцепляющийся с одним из контуров, например, с первым, можно представить следующим образом:

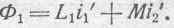
Так как силы токов равны, то, принимая во внимание выше­указанное соотношение между L ₁ L ₂ и М, можем написать:

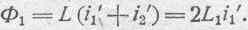
В силу того, что магнитный поток, сцепляющийся с рассматри­ваемым сверхпроводящим контуром (первым), все время сохра­няется неизменным, и разумея под i ₁ начальную силу тока в этом

контуре, когда он был беспредельно удален от второго контура, мы можем написать следующее соотношение:

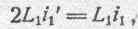
откуда получаем

и аналогично можем написать

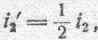
т. е. при беспредельном сближении рассматриваемых сверхпроводящих контуров сила тока в каждом из них уменьшается вдвое по сравнению с первоначальной. Принимая это во внимание, мы можем нижеследующим образом изобразить электрокинетическую энергию для случая беспредельного сближения контуров:

Мы, таким образом, видим, что в рассмотренном случае пре­дельного сближения двух сверхпроводящих контуров их электро­кинетическая энергия уменьшилась вдвое. За счет именно этого уменьшения запаса энергии в системе была совершена электро­магнитной силой механическая работа сближения контуров.

Обратим внимание на то обстоятельство, что энергия потока взаимной индукции, бывшая вначале при беспредельном удалении контуров друг от друга равной нулю, возрастает при наибольшем возможном сближении их до величины:

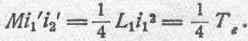
Это произошло за счет основного запаса электрокинетической энергии в системе, равного L ₁ i ₁². Половина этого запаса израсхо­дована на совершение механической работы. Половина остатка пошла на увеличение энергии потока взаимной индукции. И только

¹/₄ L ₁ i ₁² составляет в конце концов энергию обоих потоков самоиндукции:

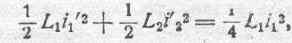
что представляет собою одну четверть первоначальной величины Т_е.

Мы видим, таким образом, что в рассмотренных случаях сверх­проводящих цепей в связи с движениями, вызываемыми электро­магнитной силой, происходит изменение сил токов и уменьшение электрокинетической энергии системы. В то же время все проис-

ходит в полном соответствии с основными законами электродина­мики. Противоречий с ними по существу никаких нет.

Случай двух сверхпроводящих контуров (при отсутствии внеш­него источника энергии) интересен в том отношении, что кажущаяся „противоречивость" получающихся в этом случае соотношений, с точки зрения ненадлежаще понимаемых классических за­конов электродинамики, т. е. уменьшение — вместо обычного увели­чения— электрокинетической энергии системы в результате движе­ния, привела американского инженера К. Геринга к заключению о необходимости пересмотра этих законов и замены их новыми, якобы более универсальными. Статьи К. Геринга по этому вопросу вызвали в свое время оживленную полемику на страницах специальных журналов. В результате выяснилось, как того и сле­довало ожидать, что максвеллова электродинамика, если только правильно пользоваться ее выводами, вполне охватывает все возможные случаи проявления электромагнитных сил.

Основная ошибка Геринга заключалась в том, что он сделал совершенно неправильный вывод из законов электродинамики. Именно, он предположил, что всегда и при всяких условиях должно иметь место реальное увеличение электрокинетической энергии. Все сказанное выше делает совершенно ясным ошибочность такого заключения.

¹) С исчерпывающей полнотой этот вопрос разобран в работе Е. А. Чернышевой и Е. Я. Семичева—„К вопросу о пересмотре некоторых основных законов электродинамики", напечатанной в журнале.Телеграфия и Телефония без проводов", 1927, № 40, стр. 71.

Дата добавления: 2014-11-29