Построение комбинационных схем (КС) по минимальным нормальным формам в различных базисах

1) Булев Базис (И, ИЛИ, НЕ)

_ _ _ _ _ _ _

y=x₁x₂x₃vx₁x₂x₄vx₁x₅vx₆ (МДНФ)

-------- ------- -----

и (3) и (3) и (2)

Схема с парафазными входами

S_Q=3+3+2=12 S^a<S_Q<S^b S^a=9 S^b=9+4=13

В общем случае задержка Т=2t (схема 2-х уровневая).

При построении схемы по МКНФ элементами 1-го уровня будут ИЛИ, а 2-го И.

Схема с однофазными входами

S_Q=16 T=3t

В общем случае задержка схемы с однофазными входами составляет 3t.

При построении схемы с однофазными входами целесообразно выбирать такую минимальную форму (если она не единственная) которая содержит наименьшее число инверсий над разными элементами.

При наличии единственной минимальной нормальной формы можно осуществить ее преобразование с использованием закона двойного отрицания и двойственности (Де Моргана)

ººº===ºººº==º===ºº ººº=--ºººº-º==-ºº

y=x₁x₂x₃ v x₁x₂x₄ v x₄x₅ v x₆= x₁x₂x₃* x₁x₂x₄* x₄x₅* x₆=

-------------------------------------------

=(x₁v x₂v x₃)(x₁v x₂v x₄)(x₄v x₅)* x₆

Для реализации этой схемы понадобятся три инвертора.

По сравне6нию с предыдущей схемой цена уменьшается на единицу (S_Q=15). Однако наличие выходного инвертора приведет к увеличению цены схемы T=4t.

2) Сокращенный булев базис (И, НЕ).

При использовании этого базиса необходимо из используемого выражения удалить все операции дизъюнкции, заменив их на конъюнкции и отрицания.

Используя предыдущие преобразования можно построить схему как с парафазными так и с однофазными входами.

Схема с парафазными входами:

S_Q=16 T=4t

При построении схемы на элементах базиса И, НЕ по МДНФ задержка схемы в общем случае составляет 4t. А при использовании однофазных входов 5t.

3) Универсальные базисы И-НЕ и ИЛИ-НЕ (см. Практику).

Задача факторизации (факторного преобразования) булевой функции.

Факторизация булевой функции сводится к вынесению за скобки общих частей термов, что, как правило, приводит к уменьшению цены синтезируемой схемы.

_ _ _ _ _ _ _ _ _ _ _ _

y=x₁x₂x₃ v x₁x₂x₄ v x₄x₅ v x₆= x₁x₂(x₃v x₄)v x₄x₅v x₆=

S_Q=12 S_Q=10 T=3t

_ _ _ _ _ _ _ _ _

= x₁(x₂x₃v x₂x₄ v x₅)vx₆= x₁(x₂(x₃v x₄)v x₅)vx₆

T=4t S_Q=11 T=5t S_Q=10

Решение задачи факторизации приводя к уменьшению цены схемы увеличивает ее задержку.

_ _ _ _ _

1) y= x₁x₂(x₃v x₄)v x₄x₅v x₆ S_Q=10 T=3t

_ _ _ _

2) y= x₁(x₂(x₃v x₄)v x₅)vx₆ T=5t S_Q=10

В тех случаях, когда схема синтезируется при ограничении на число входов в элементы, равное 2, предпочтение следует отдавать скобочной форме 2.

1)

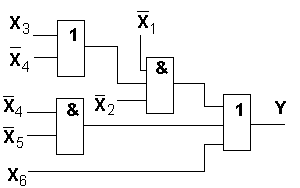
S_Q=10 T=3t

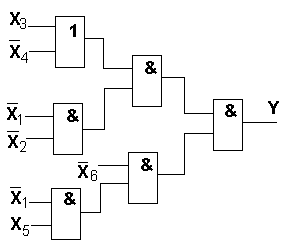
T=3t S_Q=10 К_вх=2

2)

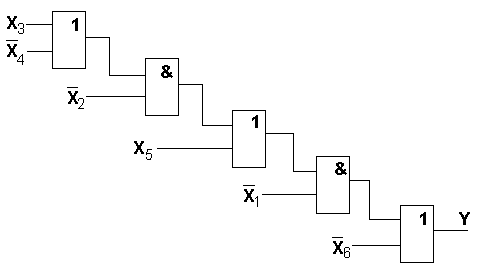
T=5t S_Q=10 К_вх=2

Схема построенная по схеме 2 удовлетворяет ограничению на число входов и является более предпочтительной по сравнению со схемой 1 по критерию цены схемы, а по критерию минимальной задержки - лучше схема 1.

Пример факторного преобразования для МКНФ

_ _ _ _

y=(x₁vx₂vx₃)(x₁vx₂vx₄)(x₁vx₅)= S_Q=11

_ _ _

=(x₁vx₂vx₃ x₄)(x₁vx₅)= S_Q=9

_

=x₁v(x₂vx₃)(x₂vx₄) x₅= S_Q=9

_ _

= x₁v(x₂vx₃ x₄) x₅= S_Q=8

Дата добавления: 2014-11-29