Декомпозиция булевых функций

Построение одновыходных схем.

Оценка эффекта факторизации.

Этот эффект характеризуется разностью цен схемы до и после факторизации.

Можно показать, что для однократной факторизации ее эффект определяется выражением:

DS_Q= S_Q^до - S_Q^после=m(k-1)+q-D,

где m - количество букв, выносимых за скобки;

k - количество термов, из которых происходит вынесение. q - количество термов, в которых после вынесения осталась одна буква (q£k);

D=1, если вынесение осуществляется из всех термов;

D=2, если не из всех.

Для эффективного решения задачи факторизации необходимо учитывать следующий момент:

1) При наличии у булевой функции нескольких минимальных форм целесообразно выбрать из них такие, для которых применение факторизации даст выигрыш в цене схемы.

2) При минимизации не полностью определенной булевой функции может оказаться, что максимальный эффект за счет факторизации дает нормальная форма, не являющаяся минимальной.

Пример:

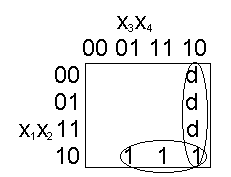
|10x1 _ _

c_min(f)=|xx10 МДНФ y=x₃x₄vx₁x₂x₄ S_Q=7

|10x1 _ _ _

c_min(f)=|101x ДНФ y= x₁x₂x₄ vx₁x₂ x₃= x₁x₂(x₃v x₄) S_Q=5

В некоторых случаях максимального эффекта за счет факторизации можно достичь путем расширения термов МНФ с применением законов товтологии

МДНФ y=x₁x₂x₃vx₁x₂x₄vx₁x₃x₅x₆vx₂x₄x₅x₆= S_Q=18

= x₁x₂(x₃v x₄)v x₅x₆(x₁x₃v x₂x₄)= S_Q=16

= x₁x₂(x₁x₃v x₂ x₄)v x₅x₆(x₁x₃v x₂x₄)= S_Q=20

=(x₁x₃v x₂ x₄)(x₁x₂v x₅x₆) S_Q=14

Задача декомпозиции булевой функции в общем случае состоит в таком разделении множества ее аргументов на ряд подмножеств, при котором можно выразить исходную функцию f(x) через вспомогательную промежуточную функцию j(z), где zÌx.

В частном случае имеет место так называемая простая разделительная декомпозиция, при которой множество аргументов x разделяется на два непересекающихся подмножества (z,w®(zÇw=j;zÈw=x)) и приведение исходной функции к виду f(x)=f(j(z,w)).

Пример: f³(x)=V(1,2,4,7)

(f=1)

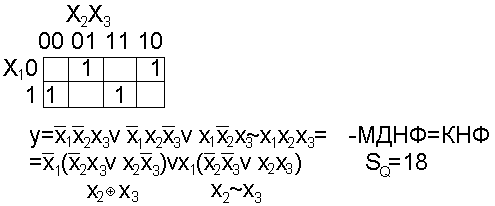
z=(x₂x₃) W={x₁}

_ _

j(z)=x₂x₃vx₂x₃

_ _

f(x)=x₁j(z)vx₁j(z) S_Q=13

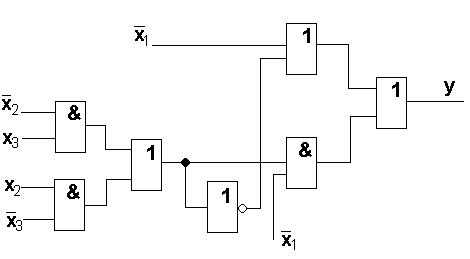
S_Q=13 T=5t

Схема базиса Жигалкина.

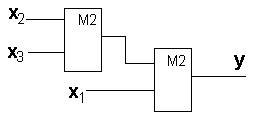
S_Q=4 T=2t

Применение декомпозиции там, где он уместно, во многих случаях позволяет уменьшить цену синтезируемой схемы.

_ _ _ _ _ _ _ _ _ _

МДНФ y=x₁x₂x₃x₄vx₂x₅vx₃x₅vx₄x₅=x₁x₂x₃x₄vx₅(x₂vx₃vx₄)

S_Q=14

_

j(z)=x₂vx₃vx₄

___ _

f(x)=x₁*y(z)vx₅*j(z) S_Q=10

Дата добавления: 2014-11-29