CRC коды 2 страница

Наименьшее положительное целое z, для которого β^z = 1, равно одному из делителей 2^m-1. Это число z называют порядком элемента. Примитивными элементами поля являются все такие элементы β = αⁱ, 0 ≤i≤ 2^m- 2, для которых i взаимно просто с числом 2^m-1.

Неприводимый многочлен называют примитивным, если его корни имеют максимальный порядок, т.е. 2^m — 1. Все корни неприводимого многочлена имеют одинаковый порядок. Периодом многочлена называют наименьшее число z, при котором р(х) делит бином x^z— 1, z|(2^m - 1). Период неприводимого многочлена совпадает с порядком его корней.

Пример 27. Примитивный полином р(х) =х³ + х + 1 порождает поле GF(2³). Примитивный элемент поля обозначим α, р(α) = α³+ α + 1 = α + 1+ α + 1 = 0. В таблице показаны три способа представления элементов поля GF(2³).

Степень	Полином	Вектор	Степень	Полином	Вектор
-			α^3	1+ α
			α^4	α + α^2
α	α		α^5	1+ α + α^2
α^2	α^2		α^6	1+ α^2

Для сложения элементов в GF(2^m) наиболее удобно векторное представление. При этом используются поразрядное сложение по модулю два. Однако для умножения в поле наиболее удобно степенное представление. В этом случае умножение сводится к сложению показателей степени элементов по модулю 2^m-1. Действительно, так как равенство αⁿ= 1, n= 2^m— 1, выполняется для всех элементов поля, то αⁿ⁺¹ = α, αⁿ⁺² = α², и т.д. Таким же способом находим, что α^-1= α^-1+n= α^n-1.

В Примере 27 α^-1 = α⁶. В общем случае, обратный элемент β^-1 = α^b элемента β = α^k определяется из сравнения b + k ≡ 0 mod(2^m — 1). Таким образом, b = 2^m - 1-k. Наконец, для реализации сложений в степенном представлении полезно использовать равенство р(α) = 0. Например, в Примере 27 имеем α³ = α³ + (α³ + α + 1) = α + 1.

Полиномиальное представление может быть удобным, когда требуется реализация вычислений по модулю некоторого полинома. Примером этого может служить декодирование циклических кодов, где требовалось вычисление xⁱ mod g(x).

Примечание: На самом деле, наиболее естественным представлением элементов конечного поля являются вычеты, т.е. остатки от деления по модулю неприводимого многочлена. В этом случае арифметика поля определяется как сложение, умножение и деление многочленов по неприводимому модулю. Если р(х) примитивный многочлен, то примитивным элементом поля вычетов по модулю р(х) является многочлен х. Иначе, все ненулевые элементы поля могут быть записаны как вычеты xⁱ mod p(x), где i=0,1,...,2^m-2.

Дополнительного пояснения требует только операция деления, или точнее, вычисление обратного элемента по неприводимому модулю. Пусть f(x) некоторый (ненулевой) вычет, тогда его обратным элементом 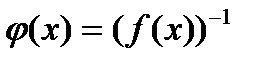называется решение сравнения

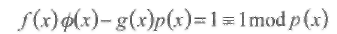
Решение этого сравнения можно найти с помощью алгоритма Евклида для вычисления наибольшего общего делителя многочленов или вычисления подходящей дроби для отношения [р(х) /f(x)J.

Таблицы логарифмов и антилогарифмов (степеней)

Удобным способом реализации умножений и сложений в конечном поле является применение таблиц с различной интерпретацией их входного адреса. Эти таблицы позволяют легко переходить от полиномиального к степенному представлению элементов поля и наоборот.

Таблица антилогарифмов (точнее, степеней) A(i) удобна для реализации сложения. Выходом таблицы является двоичный вектор, записанный как целое число, A(i), соответствующее элементу αⁱ. Таблица логарифмов (или индексов) L(i) удобна для реализации умножения в конечном поле. Эта таблица выдает значение показателя степени примитивного элемента альфа, α^L(i) соответствующего двоичному вектору, представленному целым числом i. Справедливо следующее равенство

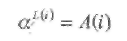
Рассмотрим пример использования таблиц для реализации арифметики конечного поля.

Пример 28. Рассмотрим поле GF(2³) с порождающим многочленом р( α )= α³ + α + 1 и α⁷= 1. Таблицы логарифмов и антилогарифмов имеют вид:

Адрес входа i	Анти - логарифм A(i)	Логарифм L(i)
		-1

Примечание. В приведенной таблице имеются две особых точки. Нулевой элемент конечного поля не может быть представлен степенью примитивного элемента. Так что в столбце «Антилогарифм» не должно быть нулевого элемента поля, а в столбце «Логарифм» нулевому элементу поля не должно быть сопоставлено какое-либо число. Таким образом, при работе с этими таблицами требуется специальная проверка на нулевой элемент поля в результате вычислений или в исходных данных.

Рассмотрим вычисление элемента γ = α(α³ + α⁵)³ в векторной форме. Учитывая свойства поля GF(2³), находим последовательно:

С использованием таблиц эти вычисления выглядят следующим образом:

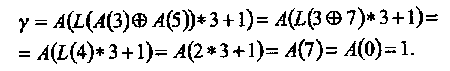
Таблицы логарифмов и степеней (антилогарифмов) используются для реализации арифметики конечного поля и GF(2^m). Соответствующие компьютерные программы доступны на ЕСС веб сайте для моделирования алгоритмов кодирования и декодирования кодов БЧХ и PC с арифметикой в GF(2^m). Сами алгоритмы рассматриваются в следующих ниже разделах.

Дополнительные свойства GF(2^m)

Минимальным многочленом ф_i(х) элемента αⁱназывается многочлен минимальной степени, корнем которого является данный элемент поля. Следующие свойства минимальных многочленов легко могут быть доказаны. Минимальный многочлен ф_i(х) элемента αⁱимеет двоичные коэффициенты и является неприводимым над GF(2) = {0,1}. Более того, корнями этого многочлена являются αⁱ, α ²ⁱ, α⁴ⁱ,..., α^τ, где τ = 2^к и kделит m. Эти элементы называются сопряженными с αⁱэлементами поля. Степени сопряженных элементов поля образуют циклотомический смежный класс

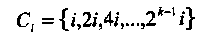
Очевидно, что степень минимального многочлена равна числу элементов (мощности) соответствующего циклотомического смежного класса, т.е.

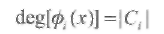
Циклотомические смежные классы (называемые также циклическими множествами) обладают свойством расщепления множества вычетов целых чисел Z_n по модулю п = 2^т - 1. Таким образом, циклотомические смежные классы не пересекаются. Иначе, их пересечение 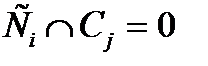, является пустым множеством, а их объединение равно всему множеству, т.е. .

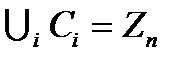Пример 29. Циклотомическими множествами по модулю 7 являются:

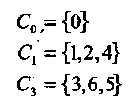
Примитивный элемент αполя GF(2^m) (как и все другие) удовлетворяет уравнению α ^п = 1. Все ненулевые элементы поля являются некоторой степенью примитивного элемента. Таким образом, бином степени п = 2^т - 1 имеет следующее разложение на неприводимые двоичные сомножители в двоичном поле:

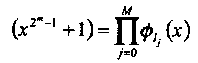
где М число циклотомических классов, и следующее полное разложение на сомножители первой степени в поле GF(2^m)

(3.9)

Важно отметить, что степень минимального многочлена ф_i(x) равна мощности (т.е. числу элементов множества) циклотомического класса С_i. Отсюда следует способ нахождения всех неприводимых делителей бинома (х^п + 1):

Найти все циклотомические классы по модулю 2^т - 1.

Для каждого циклотомического класса C_s вычислить минимальный многочлен

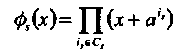(3.10)

Этот способ может быть использован для построения порождающих многочленов циклических кодов.

Пример 30. Рассмотрим поле GF(2³), порождаемое примитивным многочленом р(х) = х³ + х + 1. Корни каждого из делителей бинома х⁷ + 1 = (х+1)() показаны в таблице.

Так (x+α)(x+ α²)(x+ α⁴) = x³+x+1, а (x+α³)(x+ α⁶)(x+ α⁵) = x³+x² +1 с учётом того, что α⁶ =1+α², α³ =1+α и т.д. (смотри таблицу в примере 27).

Покажите, что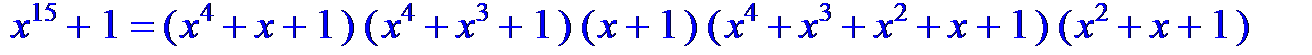

имеет следующие циклотомические классы С₀={0}; С₁= {1,2,4,8}; C₃={3,6,12,9}; C₅={5,10}; C₇={7,14,13,11}

Примитивные многочлены до степени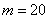

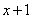
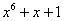
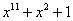
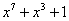
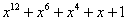
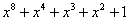
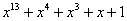
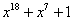
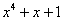
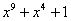
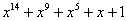
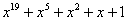
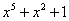
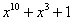
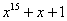
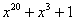
3.3. Двоичные коды БЧХ

Коды БЧХ это двоичные коды, конструкция которых определяется заданием их нулей, т.е. корней порождающего их многочлена:

БЧХ код с кодовым расстоянием d_min ≥2t_d+1 является циклическим кодом, порождающий многочлен g(x) которого имеет 2t_d последовательных корней в точках a ^b, a ^b+1,…, a ^{b+ δ}, где δ = 2t_d -1.

Таким образом, порождающий многочлен двоичного (n, k, d_min) кода БЧХ имеет вид

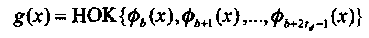
а длина и размерность кода равны, соответственно,

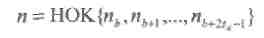
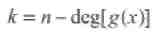
Двоичный БЧХ код, заданный таким образом, имеет конструктивное кодовое расстояние равное 2t_d + 1. Однако, следует заметить, что истинное кодовое расстояние может быть больше конструктивного.

Пример 31. Над полем GF(2³), порождаемым примитивным многочленом р(х) = х³ + х + 1, для параметров t_d = 1 и b= 1 многочлен

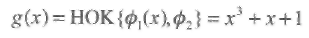
порождает двоичный (7,4,3) код БЧХ. На самом деле, это двоичный циклический код Хемминга! Заметим, что вес Хемминга этого порождающего многочлена равен 3 и, следовательно (в данном случае, но не всегда), конструктивное и истинное расстояние кода совпадают.

Пример 32. Рассмотрим поле GF(2⁴), порождаемое примитивным многочленом 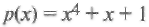, и параметры t_d = 2,b=1. Тогда многочлен

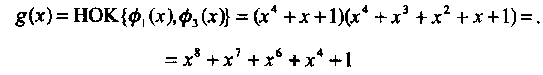
порождает двоичный (15,7,5) код БЧХ, исправляющий две ошибки.

Пример 33. В поле GF(2⁴), порождаемом примитивным многочленом р(х) = х⁴ + х + 1, и параметры t_d = 3,b= 1, многочлен

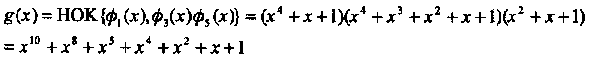
порождает двоичный (15,5,7) код БЧХ, исправляющий три ошибки.

Рассмотрим нижнюю границу минимального расстояния кодов БЧХ известную как граница БЧХ. Это полезно не только тем, что позволяет оценить корректирующие способности кода в общем случае, но и тем, что выделяет особые свойства кодов БЧХ. Напомним, что элементы a ^b, a ^b+1,, a ^{b+ δ}, где δ = 2t_d-1, являются корнями порождающего многочлена g(x) и что все кодовые слова v кода БЧХ, ассоциированные с полиномами v(x), кратны порождающему многочлену кода. Следовательно

(3.11)

Таким образом, на основании (3.11), все кодовые слова удовлетворяют следующей системе 2t_d уравнений (в матричной форме)

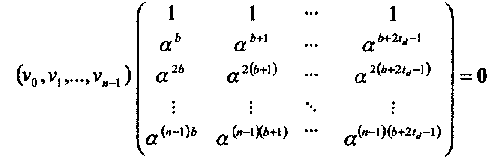(3.12)

Соответственно, проверочная матрица двоичного БЧХ кода имеет вид

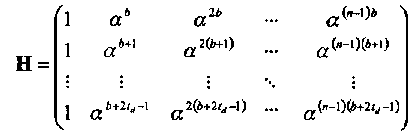(3.13)

Эта проверочная матрица обладает следующим свойством: любая ее 2t_d * 2t_d подматрица, т.е. образованная любыми 2t_d столбцами, является матрицей Вандермонда. Следовательно, любые 2t_d столбцов проверочной матрицы линейно независимы. Отсюда следует, что минимальное кодовое расстояние этого кода удовлетворяет неравенству d > 2t_d + 1. Этот результат можно интерпретировать следующим образом:

Граница БЧХ. Если порождающий многочлен g(x) циклического (n,k,d) кода имеет zпоследовательных корней, например, a^b,a^b+1,...,a^b+z, тo d≥2z+ l.

3.4. Полиномиальные коды

Класс циклических полиномиальных кодов включает циклические коды Рида-Маллера, коды БЧХ и Рида-Соломона, коды над конечными геометриями. Задание полиномиальных кодов связано с наложением условий на их корни (нули) следующим образом.

Пусть а примитивный элемент поля GF(2^ms). Пусть s положительное целое число и b делитель 2^s — 1. Тогда a^h является корнем порождающего полинома g(x) полиномиального кода порядка µ, если и только если b делит h и

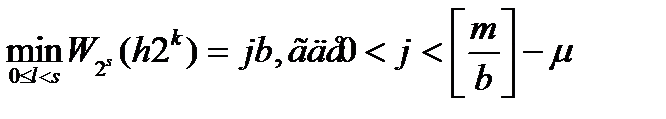
где для любого целого i,

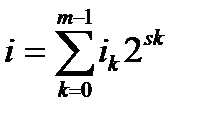
функция Wa(s) определена как (a(s) = 2s) - иначе вес целого числа i, т.е.

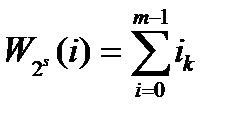
Согласно этому определению коды БЧХ и Рида-Соломона являются полиномиальными с параметрами b = т = 1. Коды Рида-Маллера является подкодами полиномиальных кодов с параметром s=1. Коды над конечными геометриями возникают как дуальные к полиномиальным кодам. Ниже даются свойства нулей конечно-геометрических кодов.

Евклидово геометрические (ЕГ) коды

Пусть а примитивный элемент поля GF(2^ms). Пусть h неотрицательное целое меньше 2^тs-1. Тогда а^h является корнем порождающего многочлена g(x) ЕГ кода порядка (µ,s), длины 2^ms-1, если и только если

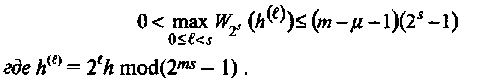
Для s = 1 ЕГ коды совпадают с циклическими РМ*_m,µ, кодами и, следовательно, ЕГ коды можно рассматривать как обобщенные коды РМ (Рида-Маллера).

Проективно геометрические (ПГ) коды

Пусть а примитивный элемент поля GF(2(^m+1)^s). Пусть h неотрицательное целое меньше 2(^m+1)^s - 1. Тогда a^h является корнем порождающего многочлена g(x) ПГ кода порядка (µ,s), длины (2^тs — 1)/(2^s - 1), если и только если h делится на 2^s - 1 и

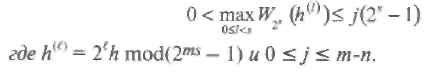
3.5. Декодирование двоичных БЧХ кодов

Главной идеей в декодировании БЧХ кодов является использование элементов конечного поля для нумерации позиций кодового слова (или, эквивалентно, в порядке коэффициентов ассоциированного многочлена). Такая нумерация показана на Рисунке 20 для вектора r = (r₀, r₁ ,..., r_n-1), соответствующего многочлену r(x).

Позиции ошибок могут быть найдены из решения системы уравнений в поле GF(2^m). Эти уравнения можно получить, вводя многочлен ошибок е(х) и учитывая нули кода а ^j для b ≤ j < b + 2t_d - 1, как показано ниже.

Пусть r(x) = v(x) + е(х) представляет полином, ассоциированный с принятым словом, где многочлен ошибок определен как

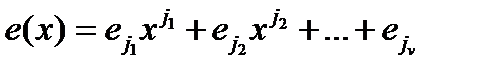(3.14)

где v ≤ t_d число ошибок в принятом слове. Множества

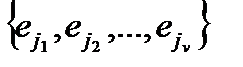и

называют значениями ошибок и локаторами ошибок, соответственно, где e_j 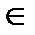{0, 1} для двоичных БЧХ⁵ кодов и 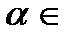GF(2^m).

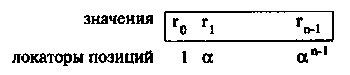
Рис. 20. Нумерация позиций кодового слова элементами поля GF(2^m)

Синдромы определены как значения принятого полинома r(х)в нулях кода:

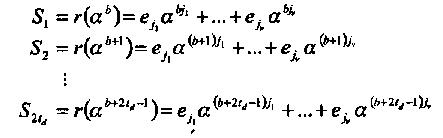
Это определение эквивалентно s = Нr, где проверочная матрица Н определена в (3.13).

Введем многочлен локаторов ошибок

(3.15)

корни которого равны обратным величинам локаторов ошибок. Тогда справедливо следующее соотношение между коэффициентами многочлена локаторов ошибок и синдромами:

(3.16)

Решение ключевого уравнения, представленного в (3.16), требует довольно интенсивных вычислений в процедуре декодирования БЧХ кодов. Известны следующие методы решения ключевого уравнения:

1. Алгоритм Берлекемпа-Мэсси (ВМА) Этот алгоритм был предложен Берлекемпом и Мэсси. По числу операций в конечном поле этот алгоритм обладает высокой эффективностью. ВМА обычно используется для программной реализации или моделирования кодов БЧХ и PC.

2. Евклидов алгоритм (ЕА)

Из-за высокой регулярности структуры этого алгоритма его широко используют для аппаратной реализации декодеров БЧХ и PC кодов.

3. Прямое решение

Этот алгоритм, предложенный Питерсоном, находит коэффициенты многочлена локаторов ошибок прямым решением системы (3.16) как системы линейных уравнений. В литературе часто используется термин PGZ (Питерсон-Горенштейн-Цирлер) декодер. В действительности, так как сложность обращения матрицы растет как куб корректирующей способности кода, прямой алгоритм может быть использован только для малых значений t_d.

3.5.1. Общий метод декодирования для БЧХ кодов

На Рисунке 21 показана блок-схема декодера БЧХ кодов (как двоичных, так и недвоичных). Декодер состоит из логических схем и обрабатывающих блоков, реализующих следующие задачи:

· Вычислить синдромы, вычисляя значения принятого полинома в нулях кода

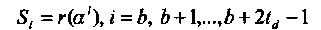(3.17)

· Найти коэффициенты многочлена локаторов ошибок σ(х).

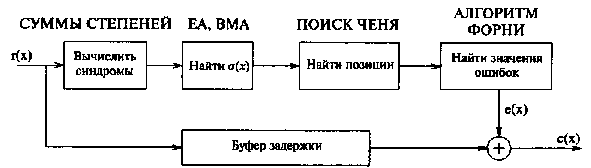
Рис. 21 Архитектура БЧХ декодера

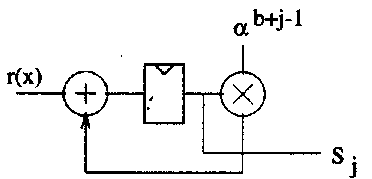
Рис. 22. Пример схемы вычисления синдрома.

· Найти обратные величины корней σ(х), т.е. позиции ошибок j₁, j₂, …, j;

· Найти значения ошибок (этап ненужный для двоичных кодов);

· Исправить принятое слово на вычисленных позициях для вычисленных значений ошибок.

Одним из преимуществ использования арифметики над конечным полем GF(2^m) является возможность применения относительно простых логических схем и вычислительных блоков. Например, на Рисунке 22 показана схема вычисления синдромов S_j. Умножение в поле GF(2^m) также реализуется относительно простой логической схемой.

3.5.2. Алгоритм Берлекемпа-Мэсси (ВМА)

Алгоритм Берлекемпа-Мэсси лучше всего рассматривать как итеративный процесс построения минимального линейного

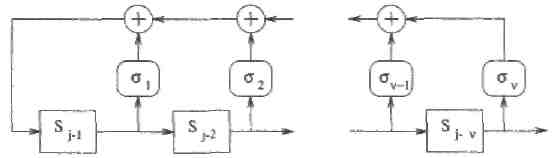
Рис. 23. ЛРОС с отводами σ₁, σ ₂,..., σ _v и выходом S₁, S₂,..., S_2v.

регистра (сдвига) с обратной связью (ЛРОС), аналогичного показанному на Рисунке 23, который генерирует известную последовательность синдромов S₁ S₂,...S_2td.

Целью ВМА является построение многочлена (обратной связи) σ ⁽ⁱ⁺¹⁾(х) наименьшей степени, удовлетворяющего следующему уравнению, выведенному из (3.16):

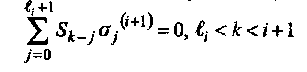(3.18)

Решение этой задачи эквивалентно условию, что многочлен

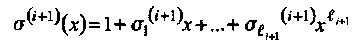
является многочленом обратной связи ЛРОС, который генерирует ограниченную последовательность синдромов.

Несовместность (рассогласование, расхождение, различие) на i -ой итерации, определенная как

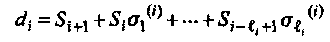
является мерой соответствия синдромной последовательности и генерируемой ЛРОС и содержит корректирующий множитель для вычисления σ (ⁱ⁺¹) на следующей итерации. Возможны два случая:

(3.19)

• Если d_i = 0, то уравнение (3.18) удовлетворяется с равенством

• Если d_i ≠ 0, то решение на следующей итерации имеет вид

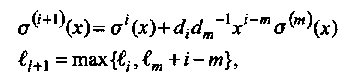(3.20)

где является решением на m-ой итерации такое, что —1 < т≤ 1, максимальна.

Итеративное вычисление σ(ⁱ⁺¹)(.х) продолжается, пока не удовлетворятся одно или оба условия: либо i ≥ 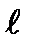_i+1,+t_d-1 либо i = 2t_d- 1.

Начальными условиями алгоритма являются:

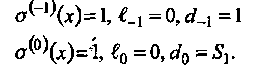(3.21)

Заметим также, что в Алгоритме Берлекэмпа-Мэсси используются программные инструкции (если — то). По этой причине ВМА не слишком удобен для аппаратной реализации. Тем не менее, по числу операций в конечном поле GF(2^W) этот алгоритм весьма эффективен.

Пример 34. Пусть С двоичный (15,5,7) код БЧХ, исправляющий три ошибки из Примера 33. Для проверки вычислений и просто для справки приводится степенное и векторное представление элементов поля GF(16), порожденное примитивным многочленом р(х) = 1 + х + х⁴:

Таблица элементов поля GF(2⁴), р(х) = 1 + х + х⁴:

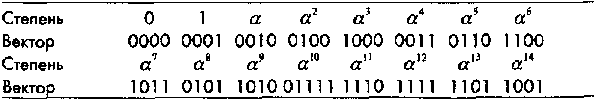
Порождающий многочлен кода С равен g(x) = х¹⁰ + х⁸ + х⁵ + х⁴ + х² + х + 1. Предположим, что информационный полином равен u(х) = х + х² + х⁴. Тогда соответствующее ему кодовое слово равно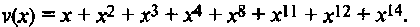

Пусть принятое слово равно r(x) = 1+х + х²+х³ + х⁴ + х⁶ + х⁸ + х¹¹ + x¹⁴, соответствующее вектору r(х) =v(х)+e(х), полученному в результате передачи слова v по ДСК. (Вектору е соответствует многочлен ошибок е(х) = 1 + х⁶ + х¹². Хотя декодеру этот вектор ошибок неизвестен, он используется здесь для упрощения вычисления синдромов.)

Синдромы равны:

Алгоритм Берлекемпа-Мэсси (ВМА):

• Итерация 0: Инициализация.

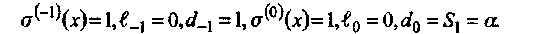
• Итерация 1:

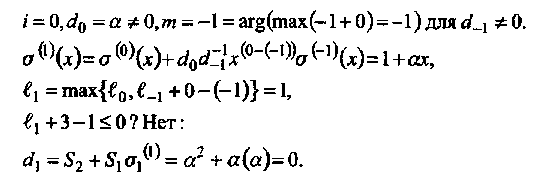
• Итерация 2:

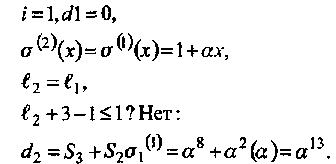
• Итерация 3:

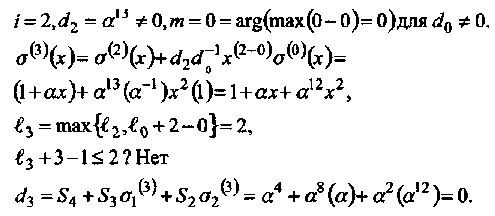
• Итерация 4:

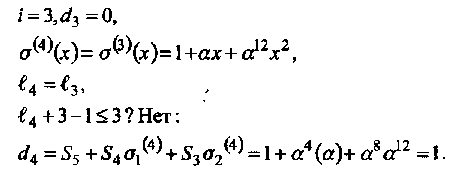
Дата добавления: 2014-11-29