Часть 4 недвоичные БЧХ коды -коды рида-соломона

В этой главе вводятся наиболее известные кодовые конструкции и объясняются алгоритмы их кодирования и декодирования. Коды Рида-Соломона (PC) нашли множество применений в системах цифровой памяти и связи. В качестве примеров упомянем знаменитый (255,223,33) код в системах космической связи НАСА (NASA), укороченные коды PC над GF(2⁸) в системах цифровой записи «компакт-диск» CD-ROM и DVD, а также в наземных цифровых системах HDTV (цифрового ТВ), расширенные (128,122,7) коды PC над GF(2⁷) для модемов на кабельных линиях, среди многих и многих других.

4.1. Коды PC как полиномиальные коды

Аналогично кодам Рида-Маллера коды PC можно определить как множество кодовых слов, компоненты которых равны значениям некоторых определенных многочленов. В действительности, это определение PC кодов принадлежит Риду и Соломону [RS]. Коды Рида-Маллера, конечно-геометрические коды [LC] и коды PC являются членами большого класса Полиномиальных кодов [PW] и тесно связаны с классом алгебро-геометрических (AG) кодов [Pre]. Обозначим

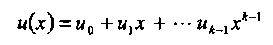(4.1)

информационный полином с коэффициентами u_i 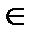GF(2^m), 10 < i < к. Очевидно, что всего имеется 2^тk таких многочленов. Вычисляя значения многочлена (4.1) для ненулевых элементов поля GF(2^m), получаем кодовое слово v кода PC с параметрами (2^m-l, к, d)

(4.2)

4.2. От двоичных кодов БЧХ к PC кодам

Коды PC можно также интерпретировать как недвоичные коды БЧХ. Можно сказать, что PC коды являются кодами БЧХ, значения кодовых символов которых взяты из поля GF(2^m). В частности, нулями PC кода, исправляющего t_d ошибок, являются 2t_d последовательных степеней примитивного элемента поля Галуа. Более того, так как над полем GF(2^m) минимальные многочлены имеют вид ф_i(х) = (х - аⁱ), 0 < i < 2^т - 1, (см. уравнение (3.9)) все делители порождающего код многочлена являются линейными (т.е. имеют степень 1) и

(4.3)

где bцелое число, обычно 0 или 1.

Из (4.3) и границы БЧХ следует, что минимальное кодовое расстояние (n,k,d) PC кода над GF(2^m) удовлетворяет неравенству d ≥ n-k +1. Из границы Синглтона [Sin], утверждающей, что d ≤ п- к + 1, следует, что d = п — к+l. Коды, удовлетворяющие последнему равенству, называют МДР кодами (кодами с максимальным достижимым расстоянием) [Sin]. Таким образом, PC код является МДР кодом. Из этого следуют полезные свойства кодов PC. Одно из них состоит в том, что укороченные коды PC являются МДР кодами.

Изоморфизм между GF(2^m) и {0,1}^m означает, что любому двоичному т - вектору х_β может быть поставлен в соответствие элемент β GF(2^m),

Другими словами, т информационных бит можно сгруппировать в блок, образующий символ GF(2^m). Если элементы GF(2^m) рассматривать как векторы из т бит, то из кода PC получаем двоичный линейный код длины п = т(2^т — 1) и размерности k = т(2^т — 1 - 2t_d). Минимальное расстояние такого кода не меньше 2t_d. Такое двоичное отображение кода PC позволяет исправлять не только до t_d случайных (двоичных) ошибок, но и многократные случайные пакеты ошибок. Например, может быть исправлен любой однократный пакет ошибок длиной до m(t_d - 1) + 1 бит. Это следует из того, что пакет ошибок длины m(q — 1) + 1 или меньше покрывается не более q символами GF(2^m). Таким образом, коды PC способны исправлять многие комбинации случайных ошибок и пакетов ошибок. В этом основная причина огромной популярности кодов PC в практических системах.

Пример 40. Пусть т=3 и поле GF(2³) генерируется примитивным элементом α, удовлетворяющим условию р( α ) = α ³ + а + 1 = 0. Пусть b= 0 и t_d = 2. Тогда имеется (7,3,5) код PC с порождающим полиномом

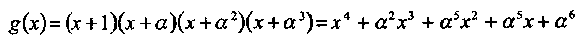
Отображением символов GF(2³) в вектора длины 3 получаем двоичный (21,9,5) код. способный исправлять до двух случайных ошибок и любой пакет до 4-х ошибок.

4.3. Декодирование кодов PC

Алгоритмы декодирования кодов PC весьма близки к алгоритмам для двоичных БЧХ кодов. Существенное различие относится только к вычислению v < t_d значений ошибок 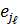, 1 < ℓ < v. В общем случае это делается с помощью алгоритма Форни [For2]. Ниже представлено выражение, справедливое для кодов PC с произвольным множеством 2t_d последовательных нулей {a^b,a^b+l,…,а^b+δ},δ = 2t_d- 1,

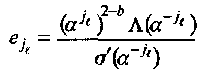(4.4)

где σ’(х) есть формальная производная по х многочлена локаторов ошибок σ(х) Многочлен Λ (х) в (4.4) это многочлен значений ошибок, определяемый как

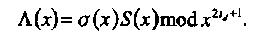(4.5)

Перед изучением первого примера декодирования кода PC мы рассмотрим другой вариант алгоритма БМ, известный как алгоритм Мэсси (или МА). Этот алгоритм был предложен Дж. Мэсси в [Mas2].

Дата добавления: 2014-11-29