CRC коды 1 страница

Один из наиболее популярных стандартов помехоустойчивого кодирования известен как избыточные циклические коды для обнаружения ошибок (CRC коды). Эти циклические коды используются для обнаружения ошибок в блоках данных. CRC коды имеют длину п≤2^т-1. Обычно CRC коды имеют порождающий полином вида (1 + x)g(x), где g(x) порождающий полином кода Хемминга. Обычные значения т равны 12, 16 и 32. Выбор порождающего полинома зависит от допустимой вероятности необнаруженной ошибки, которая определяется распределением (спектром) весов кода. Вычисление вероятности необнаруженной ошибки эквивалентно определению спектра весов кода. Эта задача остается исключительно трудной. Несмотря на 50 лет существования и развития теории кодирования имеется лишь незначительный прогресс. Ниже приведен список наиболее популярных CRC кодов (или CRC полиномов).

Код	m	g(х)
CRC-12		х^12 + х^11 +х^3 + х^2 + х+ 1
CRC-16		х^16 + x^15 + x^2 + 1
CRC-СCITT		х^16 + х^15 +х^5+ 1
CRC-32		х^32 + х^26 + х^23 + х^22 +х^16 + х^12+х^11 + х^10 + х^8 + х^7 + х^5 + х^4 + х^2 + х + 1

3.2. Общий алгоритм декодирования циклических кодов

Пусть r(х) = v(x) + e(x), где е(х) полином ошибок, ассоциированный с вектором ошибок ДСК. Тогда синдром (синдромный полином) имеет вид

s(x)= r(x) mod g(x)= e(x) mod g(x) (3.8)

На Рисунке 18 показана обобщенная структура декодера циклического кода. Синдром s(x) используется для определения полинома ошибок е(х). Так как циклический код является, прежде всего, линейным кодом, то эта структура может рассматриваться как вариант «стандартной таблицы» для циклических кодов.

Проблема декодирования равноценна поиску (неизвестного) полинома ошибок е(х) по известному синдрому s(x). Эти полиномы связаны уравнением (3.8), которое составляет основу синдромного декодера (известного также как декодер Меггита) для циклического кода. Другой (но близкий) вариант декодера, реализующий алгоритм ловли ошибок, известный также как декодер Касами, проверяет совпадение синдрома с возможным вектором ошибок. Только очень немногие классы

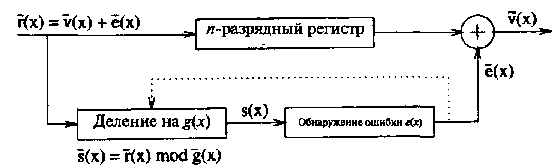
Рис. 18. Обобщенная структура декодера циклического кода.

кодов имеют такое относительно простое декодирование, как циклические коды Хемминга и Голея. Однако с увеличением корректирующей способности кода t = |_(d_min - 1)/2_| сложность декодера, основанного на комбинаторном обнаружении ошибок, становится чрезвычайно большой.

Предположим, что ошибка возникла на первой принятой позиции, т.е. е(х) = х^n-1. Соответствующий синдром равен s(x) =x^n-1 mod g(x). Если ошибка, искажающая заданную позицию, обнаруживается данным циклическим кодом, то могут быть обнаружены и ошибки на других позициях за счет циклических сдвигов и соответствующей коррекции синдрома. Синдромный декодер проверяет синдром для каждой позиции принятого слова и, если обнаруживается полином х^n-1 mod g(x), то символ на этой позиции исправляется.

Пример 25. В этом примере рассматривается декодирование циклического (7,4,3) кода Хемминга с порождающим многочленом g(x) =x³+x+l. Схема вычисления синдрома показана на Рисунке 19. Принимаемые символы накапливаются в регистре сдвига и одновременно вводятся в схему деления на g(x). После приема седьмого бита содержимое этого регистра сдвигается на один разряд в каждом такте, а схема деления модифицирует синдром и проверяет совпадение с полиномом

Как только на выходе схемы проверки появится 1, будет исправлена ошибка в позиции х⁶. В тот же самый момент исправление вводится по обратной связи в схему деления и, тем самым, обнуляет остаток от деления. Нулевой остаток может рассматриваться как сигнал об успешном завершении декодирования. Проверка на нулевой остаток схемы деления позволяет обнаруживать некоторые аномалии по окончании процедуры декодирования.

Такт	s0	s 1	s 2	Ошибочная компонента
				r 5
				r 6
				r 0
				r 1
				r 2
				r 3
				r 4

Перейдем теперь к изучению циклических кодов, исправляющих многократные ошибки, для которых задача декодирования может рассматриваться как решение системы уравнений. По этой причине здесь необходимо знакомство с полем, в котором будут выполняться операции умножения, сложения

Рис. 19. Синдромный декодер двоичного циклического (7,4,3) кода Хемминга.

и деления. Циклические коды имеют хорошую алгебраическую структуру. Позднее будет показано, что эффективная реализация мощных алгоритмов декодирования достигается при использовании арифметики конечного поля, когда известно размещение корней порождающего многочлена кода.

Напомним, что порождающий полином всегда может быть представлен произведением двоичных неприводимых многочленов:

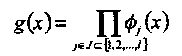
Алгебраическая структура циклических кодов выражается, в частности, в возможности определения корней каждого из многочленов в некотором поле разложения (которое является расширением поля, которому принадлежат коэффициенты многочлена). В интересующем нас случае поле разложения неприводимого многочлена является полем Галуа. В литературе поля Галуа называют также конечными полями, имея в виду конечное число принадлежащих ему элементов. Стандартным обозначением является GF(q), где q число элементов поля.

В общем случае число элементов поля есть степень простого числа, однако ниже будут рассматриваться только поля характеристики 2, когда q = 2^m.

Пример 26. В этом примере мы напомним читателям, что они хорошо знакомы с понятием «поле разложения». Рассмотрим поле действительных чисел. Известно, что в этом поле многочлен х² + 1 неприводим. Однако в поле комплексных чисел он раскладывается в произведение (х + i)(x –i), где i = 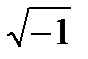. Таким образом, комплексное поле является полем разложения (т.е. расширением) поля вещественных чисел.

3.1.5 Пакеты ошибок

Характерной особенностью циклических кодов является способность к распознаванию пакетов ошибок. Под пакетом ошибок понимается группирование ошибок в одной ограниченной области кодового слова (рис. 3.16). Пакет ошибок можно описать многочленом вида

. (3.75)

Рис. 3.16. Вектор пакета ошибок длины 7.

Рис. 3.17. Вектор «концевого» пакета ошибок длины 7.

Если длина пакета ошибок не превосходит величины r = п — k, то степень многочлена ошибок меньше r. В этом случае е (Х) не делится на (Х) без остатка и синдром принятого слова всегда отличен от нулевого, следовательно, пакет ошибок длины равной или меньшей r всегда распознается. Из теоремы 3.6.1 следует, что распознается также любой циклический сдвиг многочлена В (Х) степени, меньшей r, т.е. и «концевой» пакет ошибок длины меньшей или равной r (рис. 3.17), всегда распознается.

Теорема 3.7.1. Циклический (п, k)-код способен обнаруживать все пакеты ошибок (в том числе концевые) длины r = п — k и меньше.

Помимо распознавания всех пакетов ошибок длины r и меньше циклические коды обладают способностью обнаруживать большую часть пакетов ошибок, длина которых превосходит r.

Рассмотрим пакет ошибок длины r + 1, начинающийся в j -ой компоненте. Так как первая и последняя компоненты пакета оши­бок отличны от нуля, всего имеется 2 ^{r -1} возможных конфигураций ошибок. Необнаружимой является только одна из них, многочлен которой В (Х) совпадает с (Х), то есть

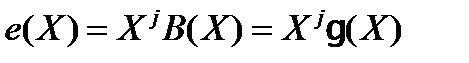. (3.76)

Теорема 3.7.2. Для циклического (п, k)-кода доля необнаружимых пакетов ошибок длины l = r + 1 = п — k +1 равна 2^{-( r -1)}.

Рассмотрим пакет ошибок длины l > r +1= n - k +1 начинающийся в j -ой компоненте. Если соответствующий многочлен В (Х) делится на (Х) без остатка, то есть

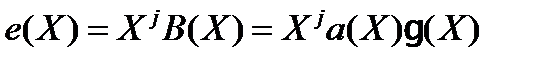, (3.77)

то такой пакет не может быть обнаружен.

Пусть коэффициенты многочлена а (Х) степени l - r - 1 имеют вид a ₀, a ₁,..., a_{l-r 1}. Так как пакет ошибок начинается и заканчи­вается единицей, a ₀ = a_{l-r- 1}. Следовательно, существует 2 ^{l-r- 2} наборов коэффициентов а (Х), приводящих к необнаружимым ошиб­кам в (3.77). С другой стороны, существует 2 ^{l- 2} различных пакетов ошибок длины l и, таким образом, верно следующее утверждение.

Теорема 3.7.3. Для циклического (п, k)-кода доля необнаружимых пакетов ошибок длины l > r + l = n — k + 1 равна 2^-r.

Пример: Распознавание ошибок циклическим (7,4)-кодом Хэм­минга.

Рассмотрим циклический (7,4)-код Хэмминга из предыдущих при­меров с r = п — k = 3. Так как минимальное кодовое расстояние кода Хэмминга dmin = 3, он способен обнаруживать все двойные ошиб­ки или исправлять одиночные. Рассматриваемый (7,4)-код Хэммин­га является циклическим кодом и он способен также обнаруживать все пакеты длины r = 3. В частности, любые три следующие друг за другом ошибки всегда обнаруживаются.

Доля необнаружимых ошибок длины r + 1 = 4 равна 2^-(3-1) = 1/4. При пакетах ошибок с длиной большей 4, не распознается только 2^-3 = 1/8 из них.

Замечание. На практике, как правило, используются циклические коды с довольно большим числом проверочных разрядов, например, r = п — k = 16. Доля необнаружимых пакетов ошибок такими кодами достаточна мала. Так, при r = 16, обнаруживается более чем 99,9969 % пакетов длины 17 и 99,9984 % пакетов длины 18 и выше.

3.2.1. Арифметика GF(q)

Множество А образует поле, если для любых элементов a_i, a_j, a_k Î А определены операции сложения «+» и умножения «´» и выполня­ются следующие аксиомы:

Сложение «+»

(А1) Замкнутость a_i + a_j Î А

(А2) Ассоциативность (a_i + a_j) + a_k = a_i + (a_j + a_k)

(A3) Существование единственного нулевого элемента 0 Î А, тако­го, что 0 + a_i = a_i

(А4) Обратный элемент (- a_i) Î А такой, что (- а) + a_i = 0

(А5) Коммутативность a_i + a_j = a_j + a_i

Умножение «х»

(M1) Замкнутость a_i ´ a_j Î А

(М2) Ассоциативность (a_i ´ a_j) ´ a_k = a_i ´ (a_j ´ a_k)

(М3) Существование единственного единичного элемента 1 Î А такого, что 1 Î a_i = a_i

(М4) Обратный элемент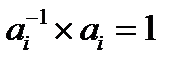

(М5) Коммутативность a_i ´ a_j = a_j ´ a_i

Сложение и умножение

(D) Дистрибутивность a_i ´ (a_j + a_k) = a_i ´ a_j + a_i ´ a_k

Из перечисленных выше аксиом следуют важнейшие правила ариф­метики, справедливые в любом поле:

Для 0,1, а, b, с Î А имеет место

1. а + 0 = 0 Þ а = 0

2. a, b ¹0 Û a ´ b ¹ 0

3. a = 0 и a ´ b = = Þ b = 0

4. -(a ´ b) = (- a) ´ b = a ´ - b)

5. a ¹ 0 и a ´ b = a ´ c /

Отметим также, что операции сложения и умножения имеют об­ратные операции: вычитания и деления, причем, вычитание опреде­ляется как а — b = а + (— b), а деление - как а ¸ b = а ´ b ^-1.

Неподготовленного читателя может смутить и даже испугать столь громоздкое аксиоматическое построение алгебраической струк­туры, называемой полем. Однако, эти страхи должны довольно быстро исчезнуть после того, как мы убедимся, что множество ра­циональных чисел образует поле. Напомним, что множество рацио­нальных чисел содержит все положительные и отрицательные целые числа (включая ноль), а также все числа вида п/т, где п, т - целые и т ¹ 0. Операциями сложения, вычитания, умножения и деле­ния в поле рациональных чисел являются обычные арифметические операции, которые мы изучали еще в начальной школе. Нетрудно заметить, что эти операции удовлетворяют всем перечисленным выше аксиомам.

Расширениями поля рациональных чисел являются поля веще­ственных и комплексных чисел, они также содержат бесконечное множество элементов.

Так как в каналах связи множество передаваемых сигналов все­гда конечно, основой теории кодирования являются поля, содержа­щие конечное число элементов (поля Галуа). Простейшим полем Галуа является двоичное поле GF (2), операции в котором (сложение и умножение) выполняются по правилам арифметики «по модулю 2». Нетрудно заметить, что правила арифметики по mod 2 удовле­творяют всем вышеперечисленным аксиомам (с учетом того, что об­ратным элементом к «1» по сложению и умножению является сама "1").

В высшей алгебре доказывается, что число элементов q конечного поля GF(q) всегда удовлетворяет условию

q = p^m, (2.55)

где р – простое число, а т = 1,2, …

Другими словами, если число элементов q некоторого множества не удовлетворяет условию (2.55), то для этого множества невозмож­но определить операции сложения и умножения, удовлетворяющие аксиомам поля. Так, например, невозможно образовать поле с чис­лом элементов, равным 6, 10, 12, 14 и т.д., но можно построить поле, с числом элементов, равным 2, 3, 4, 5, 7, 8, 9, 11 и т.д.

Таблица 2.4. Операции сложения и умножения в GF (5).

+

´

Наиболее просто операции сложения и умножения выполняются в поле с числом элементов, равным простому числу (т = 1). Здесь они определены как операции сложения и умножения по mod р, а сами элементы образуют последовательность чисел

{0,1,2,..., р -1}. (2.56)

Для примера, в таблице 2.4. приведены результаты сложения и умножения всех пар элементов a_i, b_j Î{0,1,2,3,4}, т.е сумма a_i + b_j (mod 5) и произведение a_i × b_j (mod 5). Непосредственной провер­кой можно убедиться в выполнении аксиом (Al) - (А5), (Ml) - (М5) и (D) для операций сложения и умножения. Таким образом, множе­ство элементов a Î {0,1,2,3,4} с операциями сложения и умноже­ния, заданными табл. 2.4, образуют поле GF(5).

В теории полей Галуа доказывается следующая, очень важная теорема.

Теорема 2.5.1. В поле Галуа GF (p ¹), содержащем q элементов, су­ществует по крайней мере один примитивный элемент a такой, что каждый ненулевой элемент из GF (p) может быть представлен как некоторая степень a.

Так, в поле GF (5) существует два примитивных элемента = 2 и a₂ = 3, так как 2⁰ = 1, 2¹ = 2, 2² = 4, 2³(mod 5) = 3 и 3⁰ = 1, 3¹ = 3, 3²(mod 5) = 4, 3³(mod 5) = 2.

Сложнее обстоит дело с построением полей Галуа GF (p^m), где т > 1 (простое число р называется характеристикой поля).

Так как теория кодирования имеет дело, в основном, с полями характеристики 2, рассмотрим основные методы построения полей GF (2 ^m).

Прежде всего, заметим, что каждый элемент GF (2 ^m) можно пред­ставить в виде слова длины m над GF (2) или многочлена с двоичны­ми коэффициентами, степень которого меньше, чем m. Так, напри­мер, любой элемент a Î GF (2³) можно записать как двоичное слово a ₂ a ₁ a ₀ или как многочлен a ₂ X ² + a ₁ X + a ₀, где { a ₂, a ₁, a ₀} Î {0,1}. В этом случае, сложение элементов из GF (2 ^m) выполняется по правилу сложения представляющих их многочленов в поле GF (2). Если при этом умножение элементов мы определим как умножение представ­ляющих эти элементы многочленов по модулю некоторого заданного неприводимого многочлена над GF (2) степени m, то тем самым мы построим поле Галуа GF (2 ^m).

Неприводимым называется многочлен, неразложимый на произ­ведение многочленов с коэффициентами из GF (2).

Проводя аналогию с полем GF (p), можно сказать, что роль эле­ментов GF (p) в поле GF (2 ^m) играют двоичные слова или многочле­ны степени, меньшей m, а роль простого числа р - неприводимый многочлен степени m.

Для реализации операций в поле GF (2 ^m) в качестве неприводи­мого многочлена степени m удобнее выбирать примитивный много­член.

Примитивным многочленом р (Х) над GF (2) называется непри­водимый многочлен степени m, такой, что в поле GF (2 ^m), построен­ного по его модулю, элемент поля X является примитивным.

В теории чисел и теории полей примитивный многочлен над конечным полем GF(p) —это минимальный многочлен примитивного элемента поля GF(p^m) для положительного целого числа m.

Примитивный многочлен является неприводимым.

В теории полей Галуа доказывается следующая теорема.

Теорема 2.5.2. Для каждого поля Галуа существуют примитивные многочлены всех степеней.

Таблица 2.5. Представление поля GF (2⁴) (Таблица антилогарифмов).

В качестве примера приведем поле Галуа GF (2⁴) (табл. 2.5). Для его построения был выбран примитивный многочлен четвертой сте­пени X ⁴ + X + 1. Из таблицы видно, что степени примитивного эле­мента a = X образуют все множество ненулевых элементов GF (2⁴). В таком представлении операция умножения в поле GF (2⁴) реализу­ется очень просто. Пусть, например, нам требуется найти произведе­ние элементов (1011) × (1010). Из таблицы 2.5 находим, что элемент (1011) можно представить в виде a⁷, а (1010) в виде a⁹. Из этого следует, что (1011) × (1010) = a⁷ × a⁹ = a^{(7+9) mod 15} = a¹. Используя табл. 2.5 еще раз, определяем, что a¹ соответствует элементу (0010). Окончательно получаем (1011) × (1010) = (0010).

При программной реализации умножения в полях Галуа, как пра­вило, используют так называемые таблицы логарифмов и антилога­рифмов. Таблица антилогарифмов ноля GF (2⁴) совпадает с табл. 2.5. Используя эту таблицу, очень легко определить двоичный экви­валент элемента a ⁱ по заданному i, 0 £ i £ 14. Таблица логарифмов (табл. 2.6), наоборот, позволяет быстро найти степень примитивного элемента a по его двоичному представлению.

Так как операция деления в полях Галуа эквивалентна умноже­нию на обратный элемент, весьма полезной при вычислениях ока­зывается таблица обратных элементов (табл. 2.7), которая для поля GF (2⁴) строится следующим образом. Пусть, например, нам нуж­но найти обратный элемент к (1010). По таблице логарифмов нахо­дим, что (1010) соответствует a⁹. Обратным элементом к a⁹ являет­ся a^15-9 = a⁶. По таблице антилогарифмов находим, что двоичным эквивалентом a⁶ является (1100). Таким образом, окончательно по­лучаем (1010)^-1 = (1100).

Таблица 2.6. Таблица логарифмов элементов GF(2⁴).

a^0

a^1

a^4

a^2

a^8

a^5

a^10

a^3

a^14

a^9

a^7

a^6

a^13

a^11

a^12

При небольших значениях т для ускорения умножения при про­граммной реализации можно построить таблицу умножений элемен­тов поля GF (2 ^m) размерности 2 ^т ´ 2 ^т. После того, как все необходи­мые арифметические таблицы построены, можно заменить двоичные обозначения на целочисленные.

Реализация операции сложения (и совпадающей с ней операции вычитания) элементов в поле GF (2 ^m) не представляет проблем. Сло­жение элементов из GF (2 ^m) сводится к покомпонентному сложению их двоичных представлений по модулю 2. Так, например, в поле GF (2⁴) (0011) + (1101) = (1110).

Таблица 2.7. Таблица обратных элементов поля GF(24).

a i

С подробным обоснованием построения полей GF (2 ^m) и исследо­ванием их алгебраической структуры читатель может ознакомиться в [5].

В заключение отметим, что при всей кажущейся сложности, ис­пользование полей Галуа в теории помехоустойчивого кодирования имеет глубокий математический смысл. Свойства полей Галуа поз­воляют при построении кодов использовать законы линейной алгеб­ры, справедливые для полей действительных и комплексных чисел. Отличие заключается лишь в том, что арифметические операции необходимо производить по правилам, определенным для данного конечного поля.

Используя методы абстрактной алгебры, можно показать, что в двоичном поле любой многочлен степени m раскладывается над GF(2^m). Для данного пособия достаточно ознакомиться с основами вычислений в конечных полях. Серьезным читателям настоятельно рекомендуется изучение абстрактной алгебры по хорошему учебнику.

Использование арифметики GF(2^m) в процедурах декодирования позволяет заменить сложные комбинационные схемы практичными процессорными архитектурами, пригодными для решения уравнения (3.8). Ниже приводятся инструменты, необходимые для решения систем уравнений, которые возникают при декодировании циклических кодов.

Важные свойства GF(2^m)

Поле Галуа GF(2^m) изоморфно (с точностью до знака «+») линейному пространству {0, 1}^m. Другими словами, каждому элементу β GF(2^m) соответствует единственный m-мерный вектор .

В конечном поле имеется примитивный элемент GF(2^m), степени которого порождают все ненулевые элементы поля, т.е Элемент 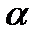является корнем неприводимого двоичного полинома р(х), р(α) = 0. Наименьшее положительное целое n, для которого αⁿ = 1, равно 2^m-1. Все элементы поля удовлетворяют уравнению βⁿ = 1, n = 2^m -1 (Другими словами, все ненулевые элементы поля совпадают с корнями степени n из единицы).

Дата добавления: 2014-11-29