Модель ДСК

Для двоичного линейного кода процедура декодирования с помощью стандартной таблицы состоит в выборе кодового слова, ближайшего к принятому слову. Ошибка декодирования возникает всякий раз, когда принятое слово оказывается вне правильной области декодирования.

Обозначим L_i число лидеров смежных классов веса i в стандартной таблице линейного кода С. Вероятность правильного декодирования равна вероятности того, что вектор ошибок совпадает с одним из лидеров смежных классов,

(1.28)

где 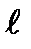это максимальный вес лидера смежного класса е. Для совершенных кодов = t,

и из границы Хемминга (1.24) следует, что

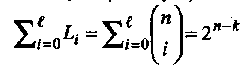
В общем случае для двоичных кодов выражение (1.28) дает нижнюю границу P_C(C), так как существует хотя бы один лидер смежного класса веса более t.

Вероятность неправильного декодирования или вероятность ошибки декодирования равна вероятности того, что вектор ошибок принадлежит дополнению множества исправляемых ошибок, т.е. P_e(C) = 1 - P_C(C). Из (1.28) получаем,

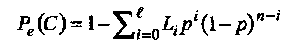(1-29)

Наконец, учитывая обсуждение оценки (1.28), получаем верхнюю границу

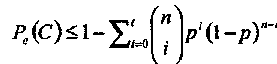(1.30)

которую можно записать и в следующем виде

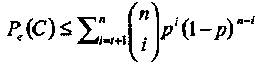(1.31)

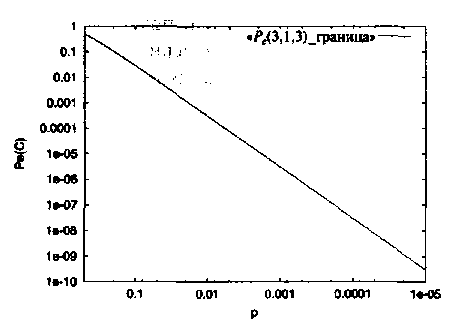
Рис. 7. Вероятность ошибки декодирования для двоичного (3,1,3) кода.

Эти границы удовлетворяются с равенством только для совершенных кодов (когда и граница Хемминга удовлетворяется с равенством).

Пример 9. На Рисунке 7 показана зависимость Р_е(С) по оценке (1.31) от переходной вероятности ДСК p для двоичного (совершенного) кода-повторения (3,1,3).

Модель канала с АБГШ Пожалуй, наиболее важной моделью для систем цифровой связи является модель канала с аддитивным белым гауссовым шумом (АБГШ - additive white Gaussian noise (AWGN)). В этом разделе выводятся оценки вероятности ошибки декодирования и вероятности ошибки на бит для линейных кодов в канале с АБГШ. Хотя аналогичные выражения оказываются справедливыми и для сверточных кодов, они будут выведены в последующих разделах, вместе с обсуждением декодирования с «мягким решением» по алгоритму Витерби. Следующие ниже результаты содержат необходимые инструменты для оценки помехоустойчивости двоичных систем кодирования в гауссовом канале.

Рассмотрим двоичную систему передачи сигналов, в которой кодовые символы {0,1} отображаются в действительные числа {+1,-1}, соответственно, как показано на Рисунке 8. В дальнейшем, вектора имеют размерность п и обозначение х = (x₀, x₁, …, x_n-1). Условная функция плотности вероятности (ф.п.в.) последовательности у на выходе канала при условии, что на его входе передавалась последовательность х, равна

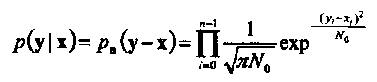(1-32)

где р_п(п) есть ф.п.в. п статистически независимых и одинаково распределенных (i.i.d.) отсчетов шума, каждый из которых имеет Гауссово распределение с нулевым средним и дисперсией, равной N₀/2. Величина N₀ называется односторонней спектральной плотностью мощности шума. Легко показать, что декодирование по максимуму правдоподобия (м.п.) линейного кода в таком канале соответствует выбору последовательности х', минимизирующей квадрат Евклидова расстояния между принятой последовательностью у и х', т.е.

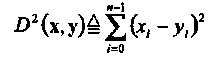(1.33)

Следует заметить, что декодер, использующий (1.33) как метрику, называется декодером с мягким решением не зависимо от того, используется или нет принцип максимума правдоподобия.

Рис. 8. Система двоичной передачи с кодированием по каналу с АБГШ.

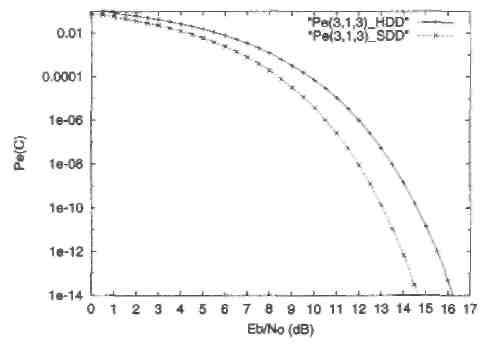
Рис. 9. Вероятность ошибки декодирования для жесткого декодирования (Pt(3,l,3)_HDD) и мягкого декодирования (Pe(3,l,3)_SDD) двоичного (3,1,3) кода при передаче двоичных сигналов в канале с АБГШ.

Вероятность ошибки для МП декодирования, Р_е(С), равна вероятности того, что при передаче последовательности х вектор шума оказался таким, что принятая последовательность у = х + n ближе к другой кодовой последовательности х" 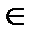С, х" ≠ х. Для линейного кода можно предположить, что передается нулевое кодовое слово. Тогда вероятность Р_е(С) может быть ограничена сверху с помощью границы объединения и распределения весов W(C) следующим образом:

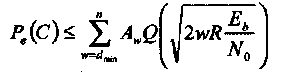(1-34)

где R = k/n скорость кода, Е_ь/N₀ отношение энергии сигнала на бит к мощности шума или (SNR на бит) и Q(x) определено в (1.2).

На Рисунке 9 показаны оценки вероятности ошибки для жесткого декодирования (1.30) и для мягкого декодирования (1.34) для двоичного (3,1,3) кода. Декодирование с жестким решением (или жесткое декодирование) означает, что декодер для ДСК использует выход двоичного демодулятора. Эквивалентный ДСК имеет переходную вероятность равную

Заметим, что в данном частном случае, обе оценки вероятности ошибки являются точными, т.е. не оценками сверху, так как используется совершенный код, содержащий только два кодовых слова. Рисунок 9 показывает также, что мягкое декодирование обеспечивает большую эффективность, чем жесткое декодирование, в том смысле, что одинаковое значение P_e(C) при меньшей мощности передачи сигналов. Разность (в дБ) между соответствующими отношениями SNR на бит обычно называют выигрышем от кодирования.

Показано, что для вероятности ошибки на бит, обозначаемой P_b(C) двоичного систематического кода при передаче двоичных сигналов по каналу с АБГШ, справедлива следующая верхняя граница:

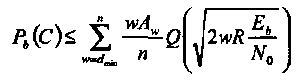(1.35)

Эта граница справедлива только для систематического кода. Кроме того, систематическое кодирование минимизирует вероятность ошибки на бит. Это означает, что систематическое кодирование не только желательно, но и оптимально в рассматриваемом выше смысле.

Пример 10. Рассмотрим двоичный линейный (6,3,3) код с порождающей и проверочной матрицами

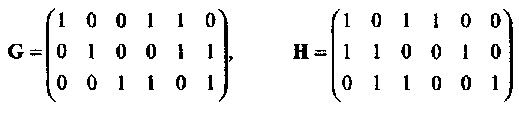
Рис. 10. Моделирование и границы объединения для двоичного (6,3,3) кода при передаче двоичных сигналов в канале с АБГШ.

соответственно. Распределение весов этого кода равно W(C) = {1,0,0,4,3,0,0}, которое может быть проверено непосредственным вычислением для всех кодовых слов v = (u,v_p):

u	vp

В этом частном случае, МП декодирование состоит в вычислении квадрата Евклидова расстояния по формуле (1.33) между принятым словом и каждым из восьми возможных кодовых слов. В качестве решения выбирается слово с наименьшим расстоянием. На Рисунке 10 показаны результаты моделирования и границы объединения для жесткого и мягкого декодирования по максимуму правдоподобия для передачи двоичных сигналов в канале с АБГШ.

Модель канала с общими Релеевскими замираниями.

Другой важной моделью канала является модель с общими Релеевскими замираниями. Замирания сигналов происходят в системах беспроводной связи в виде меняющихся во времени искажений передаваемых сигналов. В этом пособии рассматриваются только общие замирания (flat fading). Термин «общие» (или «гладкие») означает, что канал не является частотно-селективным, т.е. передаточная функция канала в полосе пропускания равна константе.

Модель канала с покомпонентными мультипликативными искажениями показана на Рисунке 11. Мультипликативные искажения представлены случайным вектором α размерности п, компоненты которого являются независимыми, одинаково распределенными случайными величинами (i.i.d.), имеющими плотность вероятности Релея,

(1.36)

При такой плотности вероятностей множителей среднее значение отношения сигнал-шум (SNR) на бит равно E_b/N₀ (как и для АБГШ без замираний), так как второй момент коэффициентов замирания равен E{a²_i } = 1.

Рис. 11 Передача двоичных кодированных сообщений в канале с гладкими Релеевскими замираниями

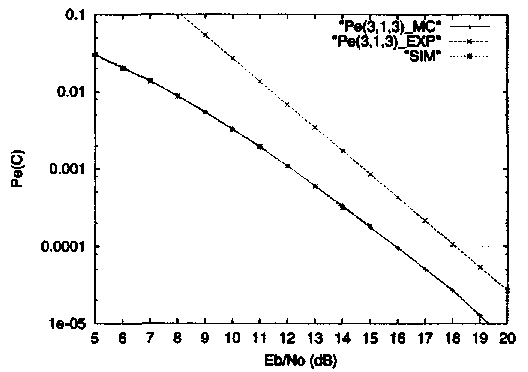
Рис. 12. Двоичная передача по Релеевскому каналу. Результаты моделирования (SIM), оценка границы объединения методом Монте-Карло (Р_е(3,1,3)_МС) и граница Чернова (Р_е(3,1,3)_ЕХР) для двоичного (3,1,3) кода.

Оценки эффективности двоичных линейных кодов в канале с общими Релеевскими замираниями находятся из оценок условной вероятности ошибки декодирования, Р_е(С\α), или условной вероятности ошибки на бит, Р_ь(С\α). Безусловные вероятности ошибки находятся интегрированием условных вероятностей с весами α_i, имеющими плотность вероятности (1.36).

Условные вероятности ошибки идентичны безусловным в канале с АБГШ. Существенное различие имеется только в аргументах функции Q(x), которые теперь взвешены на коэффициенты замирания α_i,. Рассматривая передачу двоичных кодированных сообщений при отсутствии (внешней) информации о состоянии канала, находим, что

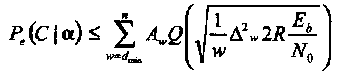(1.37)

где

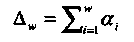(1.38)

Окончательно, вероятность ошибки декодирования при передаче двоичных сигналов в канале с Релеевскими замираниями получается как математическое ожидание относительно случайной величины ∆ _w,

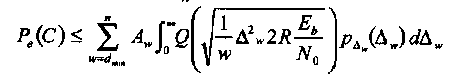(1.39)

Известны несколько методов оценивания выражения (1.39). Один из них состоит в применении метода Монте-Карло численного интегрирования с использованием следующей аппроксимации:

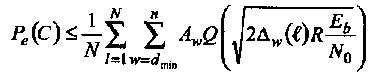(1.40)

где равно сумме квадратов w независимых одинаково распределенных (i.i.d.) случайных величин с Релеевской плотностью вероятностей (1.38), выданных на -ом обращении к компьютерной программе генерации, и N достаточно большое целое число, зависящее от ожидаемого диапазона значений Р_е(С). Хорошим правилом, которое следует запомнить, является следующее: величина N должна быть, по меньшей мере, в 100 раз больше обратной величины P_e(C).

Другим методом является экспоненциальная аппроксимация сверху функции Q, которая позволяет проинтегрировать выражение или воспользоваться границей Чернова. Этот подход хоть и несколько ухудшает результат, зато дает замкнутое выражение:

(1.41)

Рис. 13. Двоичная передача по Релеевскому каналу. Результаты моделирования (SIM_(6,3,3)),°neHKa границы объединения методом Монте-Карло (Р_е(6,3,3)_МС) и граница Чернова (Р_е(6,3,3)_ЕХР) для двоичного (6,3,3) кода.

Граница (1.41) полезна в случаях, когда достаточно знать первое приближение в оценке помехоустойчивости кода.

Пример 11. На Рисунке 12 показаны результаты компьютерного моделирования двоичного (3,1,3) кода в канале с общими Релеевскими замираниями. Заметим, что интегрирование методом Монте-Карло дает точное значение помехоустойчивости кода, так как граница (1.40) содержит только один член. Заметим также, что граница Чернова дает результат, смещенный почти на 2дБ, относительно результата моделирования при отношении сигнал-шум на бит Е_ь/N₀>18 дБ,

Пример 12. На Рисунке 13 показаны результаты компьютерного моделирования двоичного (6,3,3) кода из примера 10 в Релеевском канале. В этом случае граница объединения теряет точность при малых значениях E_b/N₀ из-за присутствия дополнительных членов в формуле (1.40). Как и раньше, граница Чернова проигрывает около 2 дБ в отношении сигнал - шум на бит при E_b/N₀> 18 дБ.

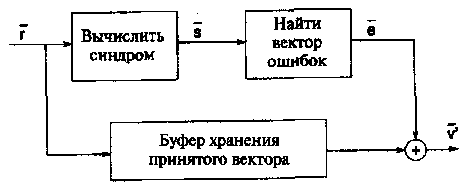
Рис. 14. Общая структура жесткого декодера для линейных блоковых кодов для ДСК.

Вопросы для самоконтроля:

1.5 Общая структура жесткого декодера для линейных кодов

В этом разделе проводится итоговое обсуждение структуры декодера с жестким решением. На Рисунке 14 показана упрощенная блок-схема процесса декодирования. Так как обсуждается жесткое решение, то решения демодулятора поступают на вход декодера, рассчитанного на работу с ДСК.

Обозначим v С переданное кодовое слово. На вход декодера подается принятое искаженное слово r = v + е. Процедура декодирования состоит из следующих шагов:

• Вычисляется синдром s = r Н^T. Согласно свойству линейного кода синдром является линейным преобразованием вектора ошибок, возникшего в канале,

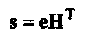(1-42)

•Для вычисленного синдрома s найти наиболее вероятный вектор ошибок е и вычесть его (по модулю два в двоичном случае) из принятого вектора.

Несмотря на то, что большинство практических декодеров не реализуют процедуру декодирования так, как она сформулирована выше, имеет смысл рассматривать процедуру жесткого декодирования как метод решения уравнения (1.42). Заметим, что любой метод решения этого уравнения является методом декодирования. Например, можно попытаться решать это (ключевое) уравнение с помощью псевдо-обратной матрицы (Н^T)⁺ матрицы Н^T такой, что Н^Т(Н^Т)⁺ = I_n и для которой результат декодирования

(1.42)

имеет наименьший вес Хемминга. Как легко бы это не казалось, задача эта очень сложна. Мы вернемся к этому соображению при обсуждении методов декодирования кодов БЧХ и Рида-Соломона.

Вопросы для самоконтроля

1. Из каких функциональных блоков состоит функциональная модель канонической цифровой системы передачи информации?

2. Чем понятие кодовая модуляция отличается от понятия помехоустойчивое кодирование?

3. Что понимают под мягким и жёстким способом построения декодера?

4. Имеет ли смысл в одной цифровой системе использовать комбинацию различных кодов исправляющих ошибки?

5. В чём состоит общая идея построения кодов исправляющих ошибки?

6. Что представляет собой кодовое слово систематического блокового кода?

7. В чём разница между блоковыми и сверточными кодами?

8. Поясните смысл понятия минимальное Хеммингово расстояния?

9. Поясните, какие параметры имеет блоковый код (п, k, d_min).

10. Найдите минимальное Хеммингово расстояние d кода (3,1,d) состоящего из двух кодовых слов (000), (111).

11. Поясните, что называют Хемминговой сферой S_t(v).

12. Поясните, что понимают под корректирующей способностью t блокового кода.

13. Запишите формулу, по которой можно определить какое максимальное количество ошибок может исправить линейный блоковый код С(n,k,d_min) в неверно принятом слове.

14. Какому принципу должно удовлетворять множество кодовых слов, чтобы код обладал свойством помехоустойчивости?

15. Что такое порождающая матрица?

16. Что такое проверочная матрица?

17. Дайте определение веса Хемминга wt_H (x)

18. Из чего состоит систематическая порождающая матрица G_sys линейного блокового кода (n, к, d_min)?

19. Из чего состоит систематическая форма проверочной матрицы H_sys линейного блокового кода (n, к, d_min)?

20. Как от порождающей матрицы G линейного блокового кода (n, к, d_min) перейти к систематической порождающей матрице G_sys этого же кода?

21. Раскройте смысл понятия скорость кода

22. Имеется двоичный линейный (4,2,2) код с порождающей матрицей 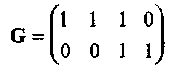запишите систематическую порождающую матрицу G_sys?

23. Имеется двоичный линейный (4,2,2) код с порождающей матрицей 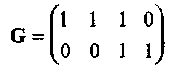запишите систематическую проверочную матрицу H_sys?

24. Имеется двоичный линейный (4,2,2) код с порождающей матрицей 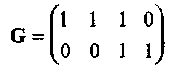запишите проверочную матрицу P.

25. Какую матрицу лучше использовать в процессе кодирования с точки зрения минимизации логических операций при скорости кода меньше 0.5.

26. Какую матрицу лучше использовать в процессе кодирования с точки зрения минимизации логических операций при скорости кода больше 0.5.

27. Что представляют собой кодовые слова, если при их создании использовались систематические формы матриц.

28. Имеется двоичный линейный (4,2,2) код с порождающей матрицей 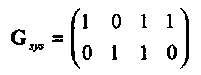запишите кодовое слово соответствующее информационному сообщению (00)?

29. Имеется двоичный линейный (4,2,2) код с порождающей матрицей 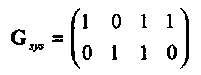запишите кодовое слово соответствующее информационному сообщению (01)?

30. Имеется двоичный линейный (4,2,2) код с порождающей матрицей 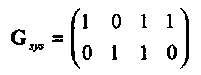запишите кодовое слово соответствующее информационному сообщению (10)?

31. Имеется двоичный линейный (4,2,2) код с порождающей матрицей 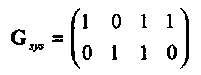запишите кодовое слово соответствующее информационному сообщению (11)?

32. Что называют стандартной таблицей (стандартной расстановкой) для двоичного линейного (n, k, d_min) кода С?

33. Как найти синдром кодового слова?

34. Имеется двоичный линейный (4,2,2) код с проверочной матрицей 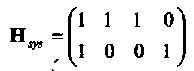запишите значение синдрома, если лидер смежного класса равен 1000?

35. Имеется двоичный линейный (4,2,2) код с проверочной матрицей 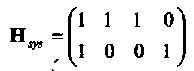запишите значение синдрома, если лидер смежного класса равен 0100?

36. Имеется двоичный линейный (4,2,2) код с проверочной матрицей 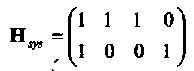запишите значение синдрома, если лидер смежного класса равен 0001?

37. Имеется двоичный линейный (4,2,2) код с проверочной матрицей 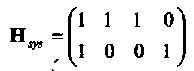запишите значение синдрома, если лидер смежного класса равен 0010?

38. Что понимают под лидером смежного класса?

39. Способен ли код (4,2,2) в принципе исправлять ошибки?

40. Какие коды называют кодами с неравной защитой от ошибок?

41. Чему равно количество слов в столбце стандартной таблицы?

42. Что такое область декодирования кодового слова?

43. Как связаны между собой корректирующая способность t кода С и множество столбцов из стандартной таблицы

44. Как определить число синдромов для линейного блокового кода С (n,k,d)?

45. Сформулируйте правило границы Хемминга

46. Имеется двоичный линейный (3,1,3) код с проверочной матрицей 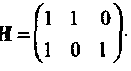запишите значение синдрома, если лидер смежного класса равен 100?

47. Имеется двоичный линейный (3,1,3) код с проверочной матрицей 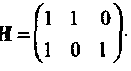запишите значение синдрома, если лидер смежного класса равен 010?

48. Имеется двоичный линейный (3,1,3) код с проверочной матрицей 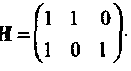запишите значение синдрома, если лидер смежного класса равен 001?

49. Имеется двоичный линейный (3,1,3) код с проверочной матрицей 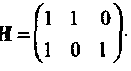запишите значение синдрома, если лидер смежного класса равен 000?

50. Какие коды называются совершенными?

51. Какие двоичные коды называются кодами Хемминга?

52. Найти распределение весов W(C) для двоичного линейного (4,2,2) кода с набором кодовых слов (0000), (0110), (1011), (1101)?

53. Дайте определение распределения весов W(С) кода С?

54. Чему равна вероятность того, что синдром принятого ненулевого искажённого кода равен нулю?

55. Дан двоичный линейный (6,3,3) код с порождающей матрицей 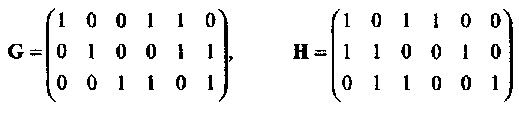найти кодовые слова соответствующие сообщениям (000) и (001)

56. Дан двоичный линейный (6,3,3) код с порождающей матрицей 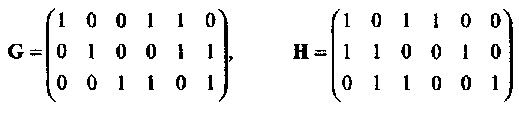найти кодовые слова соответствующие сообщениям (010) и (011).

57. Дан двоичный линейный (6,3,3) код с порождающей матрицей найти кодовые слова соответствующие сообщениям (100) и (101)

58. Дан двоичный линейный (6,3,3) код с порождающей матрицей 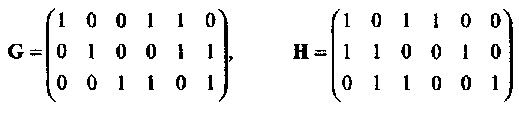найти кодовые слова соответствующие сообщениям (110) и (111)

59. Вычислить значение синдрома, если лидер класса равен (000001), а порождающая матрица равна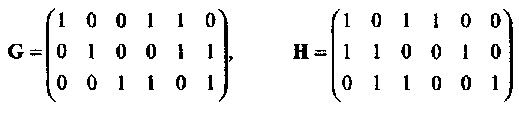

60. Вычислить значение синдрома, если лидер класса равен (000010), а порождающая матрица равна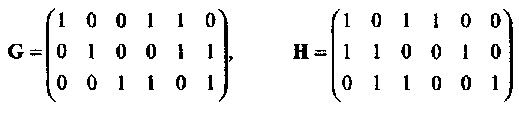

61. Вычислить значение синдрома, если лидер класса равен (000100), а порождающая матрица равна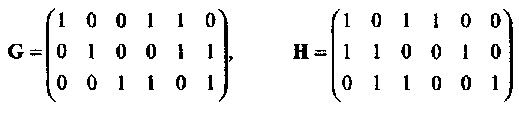

62. Вычислить значение синдрома, если лидер класса равен (001000), а порождающая матрица равна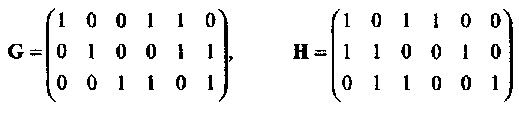

63. Вычислить значение синдрома, если лидер класса равен (010000), а порождающая матрица равна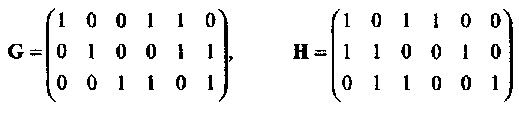

64. Вычислить значение синдрома, если лидер класса равен (100000), а порождающая матрица равна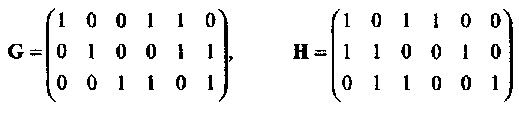

65. Найти распределение весов W(C) для кодовой последовательности (000000),(001101), (010011), (011110), (100110), (101011), (110101), (111000)

66. Опишите процедуру декодирования при структуре декодера с жёстким решением и распространением сигнала в канале ДСК

67. Опишите процедуру декодирования при структуре декодера с мягким решением и распространением сигнала в канале АБГШ

Дата добавления: 2014-11-29