Часть 2 коды Хемминга, Голея и рида-маллера

В этой части изучаются важные примеры линейных блоковых кодов. Эти примеры помогут глубже понять принципы исправления ошибок и хорошие алгоритмы декодирования. Коды Хемминга являются, по-видимому, наиболее известным классом блоковых кодов, за исключением, может быть, только кодов Рида-Соломона. Как упоминалось в части 1, коды Хемминга являются оптимальными в том смысле, что они требуют минимальную избыточность при заданной длине блока для исправления одной ошибки. Двоичные коды Голея это единственный нетривиальный пример оптимального кода, исправляющего тройные ошибки (другими примерами оптимальных кодов являются коды-повторения и коды с одной проверкой на четность). Коды Рида-Маллера представляют собой очень элегантную комбинаторную конструкцию с простым декодированием.

2.1. Коды Хемминга

Напомним (формула (1.12)), что любое кодовое слово v линейного (n, k, d_min) кода С удовлетворяет уравнению

(2.1)

Полезная интерпретация этого уравнения состоит в следующем: максимальное число линейно независимых столбцов проверочной матрицы Н кода С равно d_min - 1.

В двоичном случае, для d_min = 3, из (2.1) следует, что сумма любых двух столбцов проверочной матрицы не равна нулевому вектору. Положим, что столбцы Н являются двоичными векторами длины m. Имеется всего 2^m - 1 ненулевых различных столбцов. Следовательно, длина двоичного кода, исправляющего одиночную ошибку, удовлетворяет условию

Это неравенство в точности совпадает с границей Хемминга (1.24) для кода длины п, с п — к = т проверками и исправлением t = 1 ошибок. Соответственно, код, удовлетворяющий этой границе с равенством, известен как код Хемминга.

Пример 13. Для т=3 мы получаем (7,4,3) код Хемминга с проверочной матрицей

Как уже отмечалось, проверочная матрица кода Хемминга обладает тем свойством, что все ее столбцы различны. Если возникает одиночная ошибка на j-ой позиции, 1≤ j ≤ п, то синдром искаженного принятого слова равен j-ому столбцу матрицы Н. Обозначим е вектор ошибок, добавленный к кодовому слову в процессе его передачи по ДСК, и предположим, что все его компоненты равны нулю за исключением j-ой позиции, е_j = 1. Тогда синдром принятого слова равен

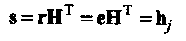(2.2)

где h_j- представляет j-ый столбец Н.

2.1.1. Процедуры кодирования и декодирования

Из уравнения (2.2) следует, что, если столбцы проверочной матрицы рассматривать как двоичное представление целых чисел, то значение синдрома равно номеру искаженной (ошибочной) позиции. Эта идея лежит в основе алгоритмов кодирования и декодирования, представленных ниже. Запишем столбцы проверочной матрицы в виде двоичного представления номера (от 1 до n) позиции кодового слова в возрастающем порядке. Обозначим эту матрицу через Н*. Очевидно, что матрице Н* соответствует эквивалентный код Хемминга с точностью до перестановки позиций кодового слова.

Напомним, что проверочная матрица в систематической форме содержит единичную подматрицу I_n-kразмера (п - k)× (п - к) как показано в (1.16). Очевидно, что в матрице Н* столбцы единичной подматрицы I_n-k (т.е. столбцы веса один) размещаются на позициях с номерами, равными степени 2, т.е. 2^z z= 0,1,..., т.

Пример 14. Пусть т = 3. Тогда систематическая (каноническая) проверочная матрица может быть задана в следующем виде

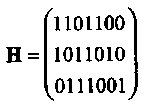
Матрица Н* заданная двоичным представлением целых чисел от 1 до 7 (младший разряд записывается в верхней строке) имеет вид:

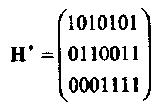
где матрица I₃ содержится в столбцах 1, 2 и 4.

В общем случае, для (2^m - 1, 2^т- 1- т) кода Хемминга и данного (арифметического) порядка столбцов единичная матрица I _т содержится в столбцах проверочной матрицы с номерами 1, 2,4,..., 2^m-1.

Кодирование

Процедура кодирования следует из уравнения (1.18). При вычислении проверочных символов p_j для всех 1 ≤ j ≤ m проверяются номера столбцов и те столбцы, номера которых не являются степенью 2, сопоставляются информационным позициям слова. Соответствующие информационные символы включаются в процесс вычисления проверок. Такая процедура кодирования в чем-то сложнее обычной процедуры для систематического (канонического) кода Хемминга. Однако, соответствующая ей процедура декодирования очень проста. Для некоторых приложений этот подход может оказаться наиболее привлекательным, так как обычно декодирование должно быть очень быстрым.

Декодирование

Если кодирование выполнялось в соответствии с матрицей Н*, то декодирование оказывается очень простым. Синдром (2.2) равен номеру позиции, в которой произошла ошибка! После вычисления синдрома s, который рассматривается как целое число s, ошибка исправляется по правилу

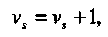(2.2)

где выполняется сложение по модулю 2 (т.е. 0+0=0, 1 + 1=0, 0+1=1,1+0=1).

Примечание. Следует заметить, что в расширенном толковании оба варианта кода Хемминга в Примере 14 являются систематическими, так как в обоих случаях известен фиксированный набор позиций кодового слова, на которых значения символов кодового слова всегда совпадают с соответствующими информационными символами. Другими словами, любые перестановки символов кодового слова оставляют код систематическим (в расширенном смысле).

Пример 14 интересен еще и тем, что Н*=РН, т.е. проверочной матрице Н*, полученной перестановкой некоторых позиций, соответствует, как оказывается, линейное преобразование исходной матрицы, где преобразующая матрица имеет вид

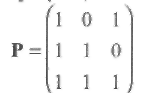
Таким образом, проверочная матрица заданного кода может иметь много различных представлений. Если еН ^Т = 0, то и еН^ТP^T = 0, где Р любая невырожденная 3×3 матрица. Если еН ^Т =s, то и eH^TP^T = sP^T =s*. Следовательно, для заданного линейного кода можно найти такое линейное преобразование его проверочной матрицы, которое окажется наиболее удобным для реализации, без каких-либо изменений самого кода. Эта возможность будет использована, например, при декодировании циклических кодов БЧХ.

Из примера 14 следует еще одно свойство линейных кодов. Пользуясь линейным преобразованием проверочной матрицы можно «назначить» проверочными любые (n - k) позиций кодового слова, если только соответствующие им столбцы матрицы являются линейно независимыми. Это означает, что по оставшимся k позициям можно однозначно восстановить все кодовое слово. Такие наборы позиций называются информационными совокупностями. Множество информационных совокупностей используется в процедурах декодирования под общим названием «ловля ошибок».

2.2. Двоичный код Голея

Голей обнаружил, что

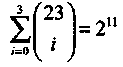
Это равенство позволяет предположить возможность существования совершенного двоичного (23,12, 7) кода с t = 3, т.е. кода, способного исправлять до трех ошибок в словах длиной 23 символа. В своей статье Голей привел порождающую матрицу такого двоичного кода, исправляющего до трех ошибок.

Из-за относительно небольшой длины (23) и размерности (12), а также небольшого числа проверок (11), кодирование и декодирование двоичного (23,12,7) кода Голея может быть выполнено табличным методом.

2.2.1 Кодирование

Табличное (LUT, look-up-table) кодирование реализуется с помощью просмотра таблицы, содержащей список всех 2¹² = 4096 кодовых слов, которые пронумерованы непосредственно информационными символами. Обозначим и информационный вектор размерности 12 бит и v соответствующее кодовое слово (23 бита). Табличный кодер использует таблицу, в которой для каждого информационного вектора (12 бит) вычислен и записан синдром (11 бит). Синдром берется из таблицы и приписывается справа к информационному вектору.

Операция LUT является взаимно однозначным отображением из множества векторов u на множество векторов v, которое может быть записано в виде

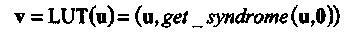(2.3)

В реализации табличного кодера учтены упрощения, которые следуют из циклической природы кода Голея. Его порождающий полином имеет вид

или в шестнадцатиричной счисления системе С75. Этот полином используется в процедуре "get_syndrome", заданной уравнением (2.3).

2.2.2. Декодирование

Напомним, что задачей декодера (Часть 1, Рисунок 14) является оценка наиболее вероятного (т.е. обладающего минимальным Хемминговым весом) вектора ошибок е по принятому вектору r.

Процедура построения табличного LUT-декодера состоит в следующем:

Выписать все возможные вектора ошибок е, вес Хемминга которых не превышает трех;

Для каждого вектора ошибок вычислить соответствующий синдром s=get_syndrome(e);

Записать в таблицу для каждого значения s соответствующий ему вектор е, так что

Исправление до трех ошибок в принятом искаженном слове r с помощью LUT-декодера может быть представлено следующим образом:

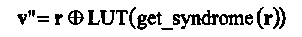
где v" — исправленное кодовое слово.

2.2.3. Арифметическое декодирование расширенного (24,12,8) кода Голея.

В этом разделе рассматривается процедура декодирования расширенного (24,12,8) кода Голея С₂₄, реализующая арифметический алгоритм декодирования. Этот алгоритм использует строки и столбцы подматрицы В проверочной матрицы Н=(В, I₁₂). Заметим, что (24,12,8) код Голея, эквивалентный с точностью до перестановки отдельных позиций коду С₂₄, может быть построен добавлением общей проверки на четность к кодовым словам (23,11,7) кода Голея.

Двенадцать строк подматрицы В, обозначенные как row_i, 1 ≤ i < 12, имеют следующий вид в шестнадцатеричной системе:

Важно отметить, что подматрица В проверочной матрицы кода С₂₄ удовлетворяет равенству В = В ^т, т.е. транспонированная и исходная матрицы совпадают. Это означает, что код С₂₄ является самодуальным кодом. Дуальным кодом называют код, использующий проверочную матрицу исходного кода в качестве порождающей.

В программе golay24.c кодирование реализуется рекуррентно, по правилу (1.18). Как и раньше, через wt_H(x) обозначен вес Хемминга вектора х. Процедура декодирования состоит в выполнении следующей последовательности шагов:

1. Вычислить синдром s = rН^T.

2. Если wt_H(s) ≤ 3, то исправляющий вектор равен е = (s, 0), перейти к шагу 8.

3. Если wt_H(s + row_i) ≤ 2, для 1 ≤ i≤ 12, то исправляющий вектор равен е = (s + row_i, х_i), где х_i вектор длины 12, содержащий 1 в i-ой координате и нули в остальных. Перейти к шагу 8.

4. Вычислить sB.

5. Если wt_H(sB) ≤ 3, то исправляющий вектор равен е = (0, sB), перейти к шагу 8.

6. Если wt_H(sB + row_i) ≤ 2, для некоторого i, 1 ≤i ≤12, то исправляющий вектор равен е = (х_i, sB + row_i), где х_i вектор длины 12, содержащий 1 в i-ой координате и нули в остальных. Перейти к шагу 8.

7. Если ни одно из условий шагов 2 - 6 не было удовлетворено, то вектор r содержит неисправимое сочетание ошибок и устанавливается флаг «отказ от декодирования». Конец процедуры.

8. Вычислить с = r + е. Конец процедуры.

Примичание. Эта процедура имеет очень простое объяснение. Кодовое слово длиной 24 символа состоит из информационной части (12) бит и проверочной части (12) бит. Если все ошибки находятся только в проверочной части, то вес синдрома равен числу ошибок. Если этот вес не превышает трех, то декодер принимает на шаге 2 процедуры декодирования однозначное решение о том, что вектор ошибок совпадает с синдромом.

На шаге 3 проверяется предположение о том, что одна (именно одна) ошибка находится на i-ой позиции в информационной части принятого слова. Для правильного выбора i прибавление row_i к синдрому компенсирует вклад этой ошибки в синдром, после чего вес измененного синдрома будет равен 2 или 1. На основании этого декодер принимает однозначное решение о том, что исправляющий вектор равен конкатенации (соединению) вектора x_i с измененным синдромом. В противном случае, число ошибок возрастет, вес синдрома не удовлетворит условию. Разумеется, может оказаться, что какое-то другое слово расположено на расстоянии не более 2 от измененного слова при условии, что в принятом слове больше трех ошибок.

На шагах 4—6 процедуры выполняются такие же проверки в предположении, что, либо все ошибки, либо все кроме одной, находятся в информационной части принятого слова. Для этого используется следующее линейное преобразование проверочной матрицы:

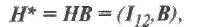
которому соответствует преобразование синдрома, равное sB.

Справедливость этого преобразования следует из равенства ВВ = I₁₂, которое легко можно проверить. Другими словами, с помощью этого преобразования, с точки зрения декодера, меняются местами информационные и проверочные позиции кодового слова, хотя никакие изменения с самим кодом не происходят.

Рассмотренная идея использована в некоторых алгоритмах декодирования, близкого к максимуму правдоподобия.

2.3. Двоичные коды Рида-Маллера

Двоичные коды Рида-Маллера (РМ) составляют семейство кодов, исправляющих ошибки, с простым декодированием, основанным на мажоритарной логике. Кроме того, известно, что коды этого семейства имеют очень простые и хорошо структурированные решетки.

Известно элегантное определение двоичных РМ кодов, основанное на двоичных полиномах (или Булевых функциях). Согласно этому определению, РМ коды становятся близкими к кодам БЧХ и PC, которые входят в класс полиномиальных кодов.

2.3.1. Булевы полиномы и РМ коды

Обозначим f(x₁, х₂,..., х_т) Булеву функцию от т двоичных переменных x₁, х₂,..., х_т. Известно, что такие функции легко представить с помощью таблицы истинности. Таблица истинности содержит список значений функции f для всех 2^т комбинаций значений ее аргументов. Все обычные Булевы операции (такие как «и», «или») могут быть представлены как Булевы функции.

Пример 15. Рассмотрим функцию f(х_1,х₂), заданную следующей таблицей истинности:

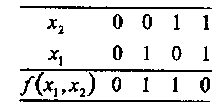
Тогда

Ассоциируем с каждой Булевой функцией f двоичный вектор f длины 2^т, составленный из значений данной функции для всех возможных комбинаций значений т ее аргументов. В последнем примере f =(0110), где принято соглашение о лексикографическом (иначе, арифметическом) упорядочении значений аргументов функции, таком, что x₁ представляет младший разряд, a x_m- старший разряд.

Заметим, что Булева функция может быть записана прямо по таблице истинности с помощью дизъюнктивной нормальной формы (ДНФ). В терминах ДНФ любая Булева функция может быть записана как сумма 2^m элементарных функций: 1, х₁, х₂, …x_m, x₁ х₂,..., х₁х_m,..., х₁х₂..х_m такой что

(2.4)

где вектор 1 добавлен для того, чтобы учесть свободный член (степени 0). В примере 15 f=x₁+x₂.

Двоичный (2^т, k, 2^т-r) РМ код, обозначенный РМ_r,m, определяется как множество векторов, ассоциированных со всеми Булевыми функциями степени до r, включительно, от mпеременных. Код PM_r,m называют также кодом РМ r-ого порядка длины 2^т. Размерность РМ_r,m кода, как легко может быть показано, равна

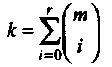
Это число равно числу способов, которыми могут быть построены полиномы степени rили меньше от mпеременных.

С учетом уравнения (2.4) строками порождающей матрицы РМ_r,m кода являются вектора, ассоциированные с kБулевыми функциями, которые могут быть записаны как полиномы степени rили меньше от m переменных.

Пример 16. Код РМ первого порядка длины 8, PM_1,3, является двоичным (8,4,4) кодом, который может быть построен из Булевых функций степени 1 от 3 переменных: {1, х₁, х₂, х₃}.Таким образом,

Порождающая матрица РМ_1,3 кода имеет, следовательно, вид

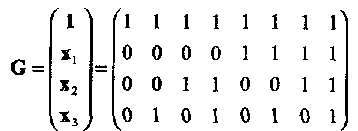(2.5)

Заметим, что код PM_1,3 может быть построен также и из кода Хемминга (7,4,3) добавлением общей проверки на четность. Расширенный код Хемминга и РМ_1,3 код могут отличаться только порядком позиций (столбцов).

Дуальные коды кодов РМ также являются кодами РМ

Можно показать, что РМ_m-r-1, _т код дуален коду PM _{r, m}. Другими словами, порождающая матрица РМ_{m-r-1, т} кода может быть использована как проверочная матрица PM _{r, m} кода.

2.3.2. Конечные геометрии и мажоритарное декодирование.

Определение кодов РМ может быть дано и в терминах конечных геометрии. Евклидова геометрия, EG(m,2), размерности т над GF(2) содержит 2^т точек, которые представляют собой все двоичные вектора длины т. Заметим, что столбцы матрицы, образованной последними тремя строками порождающей матрицы PM_1,3 кода, см. Пример 16, представляют собой 8 точек EG(3,2). Удалением нулевой точки это множество точек преобразуется в проективную геометрию PG(m-1,2). Коды над конечными геометриями являются по существу обобщением кодов РМ.

Связь между кодами и конечными геометриями можно объяснить следующим образом. Возьмем EG(m,2). Столбцы матрицы (x^T₁, х^т₂ … х^т_m)^т (где Т - операция транспонирования матрицы) рассматриваются как координаты точек геометрии EG(m,2). Тогда имеет место взаимно однозначное соответствие между компонентами двоичного вектора длины 2^т и точками EG(m,2). Заданный двоичный вектор длины 2^т ассоциируется с подмножеством точек EG(m,2). В частности, подмножество EG(m,2) может быть ассоциировано с двоичным вектором w = (w₁, w₂, …, w_n) длины п=2^т, если интерпретировать значение его координат w_i =1 как выбор точки. Другими словами, w является вектором инцидентности (совпадений).

Теперь двоичный код Рида-Маллера можно определить следующим образом: кодовыми словами PM_r,m кода являются вектора инцидентности всех подпространств (т.е. линейных комбинаций точек) размерности т-r в EG(m,2) Из этого определения следует, что число кодовых слов минимального веса РМ_r,m кода равно

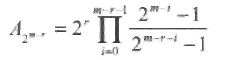(2.6)

Код, который получается после удаления (перфорации) координат, соответствующих условию х₁ = х₂ =... = х_m = 0, из всех кодовых слов PМ_r,m кода является двоичным циклическим РМ*_r,m кодом. Число слов минимального веса циклического РМ кода равно

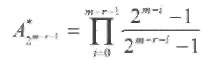(2.7)

Декодирование РМ кодов может быть выполнено на основе мажоритарной логики (МЛ). Идея мажоритарного декодирования состоит в следующем. Как известно, проверочная матрица порождает 2^п-к проверочных уравнений. Построение МЛ декодера сводится к выбору такого подмножества проверочных уравнений, чтобы решение о значении кодового символа на определенной позиции формировалось по большинству «голосов», причем каждый «голос» связан с одним из проверочных уравнений. В качестве иллюстрации рассмотрим код РМ_1,3 из Примера 16.

Пример 17. Пусть вектор является кодовым словом кода PM_1,3. Как уже упоминалось ранее, выражение (2.5) определяет порождающую, а также и проверочную матрицу PM_1,3 кода, поскольку в данном случае r= 1 и m-r-1=1 и, следовательно, код является самодуальным. Все возможные ненулевые линейные комбинации (всего 15) проверочных уравнений (строк проверочной матрицы Н) имеют вид:

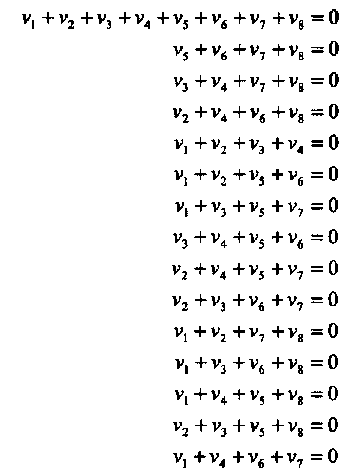(2.8)

Читателю предлагается проверить, что сумма v_i + v_j любой пары кодовых символов v_i и v_jпоявляется точно в четырех уравнениях. Более того, в уравнениях, которые содержат одинаковую сумму (v_i + v_j), любые другие суммы пар появляются не более одного раза (т.е. не более чем в одном уравнении). Такие проверочные уравнения называют ортогональными относительно пары символов v_i и v_j.

Покажем теперь способ исправления одиночной ошибки. Пусть в результате передачи кодового слова v по ДСК получен вектор

r = v + e = (r₁, r₂, r₃, r₄, r₅, r₆, r₇, r₈)

Предположим, что ошибка, которая должна быть исправлена, находится в v₅. Построим процедуру мажоритарного декодирования для данного случая.

Выберем два уравнения, включающие сумму v_i + v₅, i≠ 5, и два других уравнения, содержащие сумму v_j + v₅, j≠5, i≠j. Примем, например, i = 3 и j = 4. Имеется четыре проверки ортогональные сумме v₃ + v₅. Выберем любые две из них. Выполним тоже самое для суммы v₄ + v₅. Ассоциированные с выбранными проверками синдромы обозначим S₁ и S₂ для суммы v₃ + v₅, а также S₃ и S₄ для суммы v₄ + v₅. В результате имеем:

(2.9)

Так как вектор v является кодовым словом PM_1,3 кода, то система уравнений (2.9) эквивалентна следующей

(2.10)

Поскольку проверки S₁ S₂, S₃, S₄ ортогональны относительно е₃ + е₅ и е₄ +e₅, то может быть построена новая пара уравнений ортогональных относительно е₅.

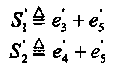(2.11)

где e'_j, j = 3, 4, 5, представляют мажоритарные оценки, полученные из уравнений (2.9). Уравнения (2.11) ортогональны относительно е'₅ и, следовательно, значение е'₅ может быть получено голосованием. Например, в данном случае это может быть результат операции «И» с входами S’₁ и S'₂

Предположим, что передавалось слово v = (111 10000) и было принято слово r = (11111000). Тогда из (2.10) получаем

(2.12)

Таким образом, оба терма е₃ + e₅ и е₄ + е₅ оцениваются равными «1». Из (2.11) получаем оценку е₅ = 1 и оценку исправляющего вектора е = (00001000). Окончательно, оценка переданного слова равна v = r + е = (11110000). Таким образом, продемонстрирован двух шаговый способ мажоритарного исправления одной ошибки на пятой позиции.

В предыдущем примере было показано, как исправляется одна ошибка в заданной позиции для кода PM_1,3 Аналогичная процедура может быть применена к любой позиции принятого слова. Следовательно, могут быть получены и все восемь мажоритарных оценок для каждого символа.

В общем случае код РМ_r,m может быть декодирован (r + 1) -шаговой мажоритарной процедурой декодирования с исправлением любой из возможных комбинаций случайных ошибок веса |_(2^{m - 2} - 1) / 2_| или меньше.

Дополнительно заметим, что циклический код РМ*_r,m декодируется несколько проще. В циклическом коде С, если (v₁, v₂,..., v_n) любое кодовое слово, то и его циклический сдвиг (v_n, v₁,..., v_n-1) тоже кодовое слово. Отсюда следует, что, если некоторая позиция может быть декодирована по мажоритарному методу, то и все n позиций будут декодированы тем же самым способом с использованием циклического сдвига.

Пример 18. В этом примере рассматривается декодер циклического PM*_1,3 кода, который совпадает с двоичным (7,4,3) кодом Хемминга. Для того, чтобы получить проверочные уравнения циклического кода из проверок PM_1,3 кода, достаточно удалить во всех уравнениях координату v₁, для которой x₁ = х₂ =...= х_m. После удаления v₁ изменим нумерацию позиций PM*_1,3 кода следующим образом:

Как и раньше, можно построить мажоритарный декодер для произвольной позиции (например, пятой), учитывая семь линейно независимых проверочных уравнений:

(2.13)

По аналогии с предыдущим примером находим, что синдромы S₁ и S₂ ортогональны относительно символов v₄ и v₅, а S₂ и S₃ ортогональны относительно v₅ и v₆:

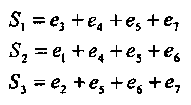(2.14)

Используя промежуточные оценки сумм v₄ + v₅ и v₅ + v₆, получаем дополнительно два ортогональных уравнения относительно v₅:

(2.15)

где e'_j, j = 4, 5, 6, обозначены мажоритарные оценки, полученные на предыдущем шаге. Этот алгоритм представлен на Рисунке 15 в виде логической схемы.

Эта схема работает следующим образом. Начальное состояние семи ячеек регистра памяти устанавливается нулевым. Предположим, что принятое слово содержит ошибку в позиции с номером i, 1 ≤ i ≤ 7. На каждом такте содержимое регистра памяти сдвигается вправо на одну позицию. Время в тактах представлено на схеме нижним индексом.

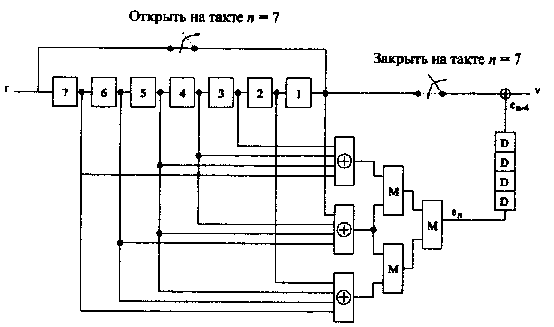
Рис. 15. Мажоритарный декодер циклического кода РМ*(1,3)

Рассмотрим случай i = 1. Это означает, что ошибка находится в первой позиции принятого слова. Через три такта эта ошибка переместится в пятую ячейку регистра (v₅). Выход мажоритарной логической схемы примет состояние е_п = 1. Еще через четыре такта (на седьмом такте) первый принятый символ попадет на выход декодера и будет исправлен. Рассмотрим теперь случай i = 7. Через девять тактов ошибка будет обнаружена и выход мажоритарной схемы примет значение е_п = 1. Спустя четыре такта (т.е. на тринадцатом такте) последний символ поступит на выход декодера и будет исправлен. Декодер, который здесь рассматривается, имеет задержку 13 тактов. Через 13 тактов содержимое регистра стирается и начинается обработка нового принятого слова.

В следующей части рассматриваются циклические коды и обширное семейство БЧХ кодов.

Вопросы для самоконтроля

Какие коды называются самодуальными?

Запишите параметры (n,k,d) двоичного кода Голея.

Что значит понятие систематический код в расширенном смысле?

Дата добавления: 2014-11-29