CRC коды 3 страница

• Итерация 5:

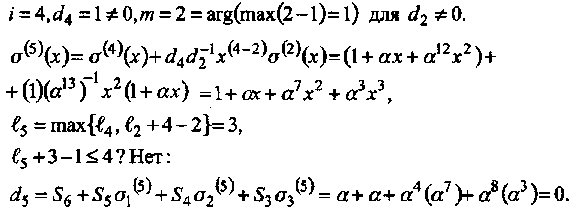
• Итерация 6:

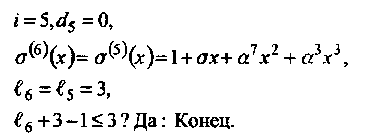
Таким образом,

То, что на нечетных шагах алгоритма d_i= 0 в предыдущем примере не случайность. Для двоичных кодов БЧХ это закономерность. С тем же результатом можно было выполнять только четные шаги алгоритма. Единственное изменение состоит в замене правила остановки на следующее

В результате снижается сложность декодирования. Читателю предлагается найти σ(х) в Примере 34, используя только три итерации.

3.5.3. Декодер PGZ

Впервые этот алгоритм был рассмотрен Питерсоном. Решение ключевого уравнения (3.16) может быть найдено с помощью стандартной техники решения системы линейных уравнений. Это решение дает коэффициенты σ(х). Применению этой техники мешает только то, что неизвестно действительное число ошибок в принятом слове. По этой причине приходится проверять гипотезу о том, что действительное количество ошибок в принятом слове равно v. Предположим, что не все синдромы S_i, 1 ≤ i ≤2t равны нулю. Очевидно, что принятое слово совпадает с одним из кодовых, если все синдромы равны нулю. Тогда процедура декодирования на этом завершается!

Декодер начинает с предположения о том, что возникло максимальное число ошибок 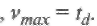Он вычисляет определитель

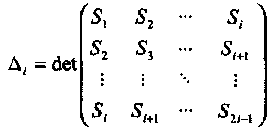(3.22)

и сравнивает его с нулем. Если определитель равен нулю, то действительное число ошибок меньше, чем предполагалось. Значение i уменьшается на единицу и снова проверяется определитель. Процедура повторяется, если это необходимо, пока i >1. Как только окажется, что определитель не равен нулю, вычисляется обратная матрица для матрицы синдромов и вычисляются значения σ₁, σ₂,..., σ _v, где v = i. В случае, когда ∆i = 0, для i = 1, 2,..., t_d, декодирование считается безуспешным и регистрируется обнаружение неисправляемой комбинации ошибок.

Пример 35. В этом примере полином локаторов ошибок для (15, 5, 7) БЧХ кода из Примера 34 находится с помощью PGZ алгоритма. Предположим для начала, что имеется i=t_d = 3 ошибки. Определитель ∆₃ вычисляется (с использованием алгебраического дополнения) следующим образом:

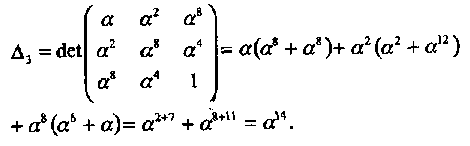
Так как ∆₃ ≠ 0, то подтверждается предположение о том, что в принятом слове три ошибки. Подставляя синдромы, найденные в Примере 34, в ключевое уравнение (3.16), получаем:

(3.23)

Напомним, что (∆₃)^-1 = a ^-14 = а. Решение уравнения (3.23) имеет вид:

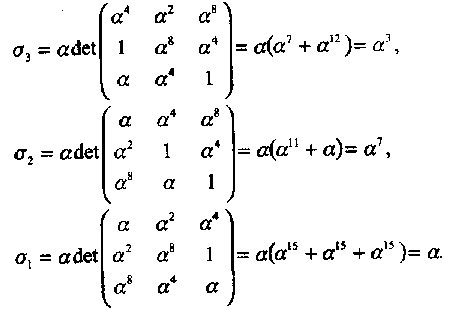
Таким образом, получили что совпадает с результатом, полученным по алгоритму БМ в Примере 34.

3.5.4. Евклидов алгоритм (ЕА)

В основе этого алгоритма лежит хорошо известная процедура нахождения наибольшего общего делителя (НОД) двух полиномов (или целых чисел). Ниже рассматривается применение ее для декодирования БЧХ кодов.

Определим полином значений ошибок как Λ(х) = σ(x)S(x), где синдромный полином имеет вид

(3.24)

Из уравнения (3.16) следует, что

(3.25)

Задача декодирования может быть переформулирована как задача определения многочлена Λ(х), удовлетворяющего уравнению (3.25). Это решение может быть найдено применением расширенного алгоритма Евклида к многочленам r₀(x) = x^d, d = 2t_d+ 1 и r₁(x) = S(x). Если нa j-ом шаге алгоритма получено решение

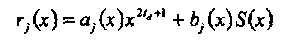
такое, что deg[r_j(x)] ≤ t_d, то Λ(х) = r_j(x)и σ_i(x)= b_j(x). Заметим, что для задачи декодирования полином а_i(х) не представляет интереса, так как решение (3.25) ищется по модулю х^d.

Расширенный алгоритм Евклида вычисления НОД состоит в следующем.

Расширенный алгоритм Евклида: Вычисление НОД(r₀(x), r₁(x))

Вход: r₀(x), r₁(x), deg[r₀(x)] > deg[r₁(x)]

Начальные условия: а₀(х) = 1, b₀(х) = 0, а₁(х) = 0, b₁ (х) = 1.

На шаге j (j ≥ 2) применить длинное деление к многочленам

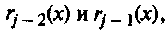
•Вычислить

a_j(x) = a_j-2(x)-q_j(x)a_j-1(x), b_j(x) = b_j-2(x)-q_j(x)b_j-1(x)

•Остановить вычисления на итерации last = j_last, когда
deg[r_last(x)]=0.

Выход: НОД(r₀(х), r₁(x)) = r_k(x), где к наибольшее ненулевое целое такое, что r _к(х) ≠ 0 и k <j_last.

Пример 36. В этом примере вычисляется полином локаторов ошибок о(х) для (15, 5, 7) кода БЧХ из примера 34 по алгоритму Евклида.

• Начальные условия:

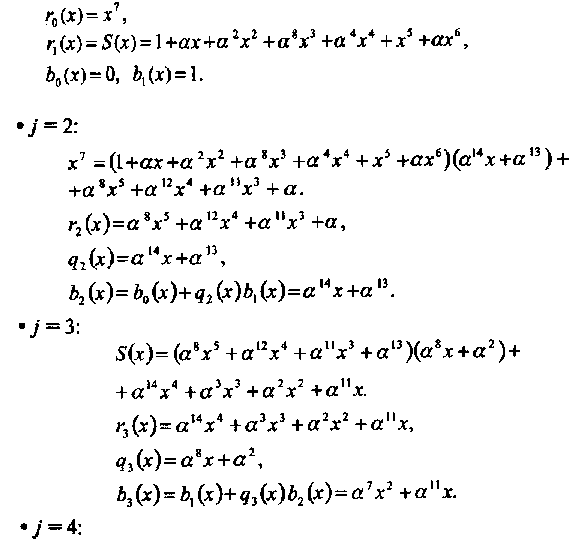
Так как deg[r₄(x)] = 1 ≤ 3, алгоритм останавливается.

Очевидно, что многочлен

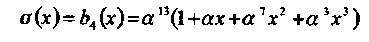
имеет те же самые корни, что и многочлены, найденные алгоритмами ВМА и PGZ (см. Пример 37 ниже), и отличается только константным множителем.

Последний пример показывает, что в общем случае многочлен локаторов ошибок, полученный алгоритмом Евклида, может отличаться на константный множитель от решения, полученного алгоритмами ВМА и PGZ. Для декодирования представляют интерес только корни этих полиномов, а не их коэффициенты. Таким образом, все три метода находят требуемый многочлен локаторов ошибок.

3.5.5. Метод Ченя и исправление ошибок

Для поиска корней σ (х) на множестве локаторов позиций кодовых символов используется метод проб и ошибок, получивший название метод Ченя. Для всех ненулевых элементов β 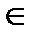GF(2^m), которые генерируются в порядке 1, a, а²,... a¹⁴ проверяется условие σ(β^-1)=0. Этот процесс легко реализуется аппаратно. На самом деле, поиск корней (факторизация) многочленов над GF(2^m) является увлекательной математической задачей, которая еще ждет своего решения.

Для двоичных кодов БЧХ исправление ошибок на позициях j₁,..., j_v, соответствующих найденным корням, сводится к инвертированию символов, принятых на этих позициях, т.е.

после чего, выдается восстановленное кодовое слово v(x).

Пример 37. Продолжая Пример 34, находим, что корни многочлена локаторов ошибок равны: 1, а⁹ = а^-6 и а³ = а^-12. Другими словами, получено следующее разложение многочлена на множители

Соответственно, восстановленный многочлен ошибок равен 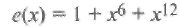и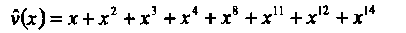

Три ошибки исправлены.

3.5.6. Исправление стираний и ошибок

Существует много ситуаций, когда решение о принятом символе не может считаться надежным. Рассмотрим, например, передачу двоичных символов по каналу с АБГШ с двоичной фазовой манипуляцией, т.е. с отображением 0→+1 и 1→ -1. Если значение принятого сигнала слишком близко к нулю, то возможно, более разумно, с точки зрения минимизации вероятности ошибки декодирования, отказаться от решения о принятом символе. В таких случаях принятый символ «стирается», а такое решение называют стиранием. Подобные стирания представляют собой простейшую форму мягкого решения.

Введение стираний, по сравнению с исправлением только ошибок, обладает тем преимуществом, что декодеру известны позиции с ненадежными символами. Пусть d минимальное кодовое расстояние, v число ошибок и µчисло стираний в принятом слове. Тогда минимальное Хеммингово расстояние по нестертым позициям снижается, по меньшей мере, до величины d-µ. Следовательно, корректирующая способность равна [ (d — µ — 1)/2] и справедливо следующее соотношение

(3.26)

Последнее неравенство, на уровне интуиции, означает, что исправление ошибок требует вдвое больше усилий (и избыточности), чем исправление стираний, поскольку позиции стираний известны.

Для двоичных линейных кодов, включая коды БЧХ, стирания и ошибки могут быть исправлены следующим ниже методом.

Записать нули на стертые позиции и декодировать полученное слово в кодовое слово обозначенное v₀(x).

Записать единицы на стертые позиции и декодировать в кодовое слово v₁(x).

Выбрать из v₀(x) и v₁(x) в качестве результата декодирования кодовое слово, ближайшее к принятому слову по нестертым позициям. Иначе говоря, в качестве результата декодирования выбирается слово, потребовавшее наименьшего числа исправлений.

Таким образом, любая допустимая по условию (3.26) комбинация стираний и ошибок исправляется за две попытки исправления ошибок.

Пример 38. Рассмотрим циклический (7,4,3) код Хемминга с порождающим многочленом g(x) = 1 + х + х³ и конечное поле GF(2³) с примитивным элементом а, удовлетворяющим условию р(а) = 1 + а + а³. Предположим, что передано слово v(x) = х + х² + х⁴ и что приемник ввел два стирания. Так как d = 3 >µ, то эти стирания могут быть исправлены. Пусть r(x) =f + х + х² + fx³ + х⁴ полином, ассоциированный с принятым словом, где через f обозначены стирания.

Первая попытка: декодируем принятое слово при f = 0, r₀(x)= х + х² + х⁴. Синдромы для него равны: S₁ = r₀(α) =0 и S₂ = (S₁)² = 0 Следовательно, v₀(x) - r₀(х) = х + х² + х⁴.

Вторая попытка: теперь декодируем при f=1, r₁ (х) = 1 + х + х² + х³ + х⁴, S₁ = а и S₂ = а². Уравнение (3.16) имеет в этом случае вид: аσ₁ = а². В результате получаем σ (х) = 1 + ах, е(х) = х и кодовое слово v₁(x) = r₁(x) + е(х) = 1 + х² + х³ + х⁴, которое отличается от принятого слова r (х) в одной нестертой позиции. В качестве результата декодирования выбираем слово v₀(x). Таким образом, исправлены два стирания.

Следует напомнить, что для исправления только стираний линейным кодом (при точном отсутствии ошибок) достаточно найти решение системы линейных уравнений r Н^т=0. Решение этой системы единственно, если число стираний меньше кодового расстояния. Кроме того, этим методом можно исправить многие из комбинаций с числом стираний больше кодового расстояния (но не более числа проверок), хотя решение может быть не всегда единственным.

3.6. Распределение весов и границы вероятности ошибки

В общем случае, распределение весов двоичного линейного (n,k) кода С может быть найдено перечислением всех 2^к кодовых слов и подсчетом их веса Хемминга. Очевидно, что при больших k это нереализуемая затея. Обозначим A_w число кодовых слов веса Хемминга w. Тождество Мак-Вильямc связывает распределение весов линейного кода, А(х) = А₀ + А₁х + А₂х² +...+ А_nxⁿ, с распределением весов дуального ему (n, n-k) кода С┴, В(х) = B₀ + В₁х + В₂х² +... + В_nxⁿ, следующим соотношением:

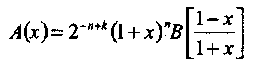(3.27)

которое может быть записано и в обращенной форме

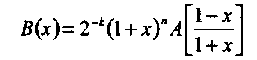(3.28)

Таким образом, для кодов с высокой скоростью проще сначала подсчитать распределение весов дуального кода, а затем вычислить А(х) по формуле (3.27).

Для некоторых классов кодов может быть использована решетчатая структура кода. Для кодов меньшей длины распределение весов нетрудно посчитать с помощью тождества Мак-Вильямс. Далее вводится определение расширенного циклического кода. Двоичный расширенный циклический код получается из циклического кода добавлением, в начале (или, наоборот, в конце) каждого кодового слова, общей проверки на четность. Расширенный код уже не является циклическим. Пусть Н проверочная матрица циклического кода, тогда проверочная матрица Н_ext расширенного кода равна

(3.29)

Для расширенных БЧХ кодов известно, что A^(ext)_n+1-w = A^(ext)._w Эти данные полезны для нахождения распределения весов двоичного циклического БЧХ кода длины до 127. Это делается с помощью следующего результата.

Пусть С двоичный циклический (п, k) БЧХ код с распределением весов А(х), полученный исключением общей проверки из двоичного расширенного (n+1, k) с распределением весов А^(eхt)(х). Тогда для четного веса w справедливо соотношение:

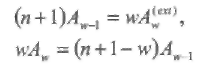(3.30)

Пример 39. Рассмотрим двоичный расширенный (8,4,4) код Хемминга. Этот код имеет проверочную матрицу (см. также Пример 23)

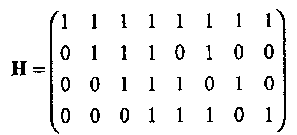
Легко проверить, что А^(ext)(х) = 1 + 14x⁴ + х⁸. Для распределения весов двоичного циклического (7, 4, 3) кода Хемминга получаем с помощью (3.30)

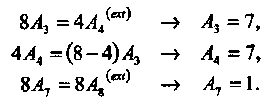
3.6.1. Оценка вероятности ошибки

Известный спектр весов кода позволяет оценить его вероятности ошибки, как это обсуждалось в части 1. Распределение весов и граница объединения (1.34) дают хорошую оценку вероятности ошибки кода при передаче двоичных сигналов по каналу с АБГШ.

На Рисунке 28 представлена граница объединения (1.40) для канала с общими Релеевскими замираниями и распределения весов из приложения А для БЧХ кода длины 8. Граница посчитана с помощью метода Монте-Карло при замене коэффициента A_w на wA_w/n чтобы учесть двоичные ошибки. Границы для других кодов могут быть получены аналогичным способом.

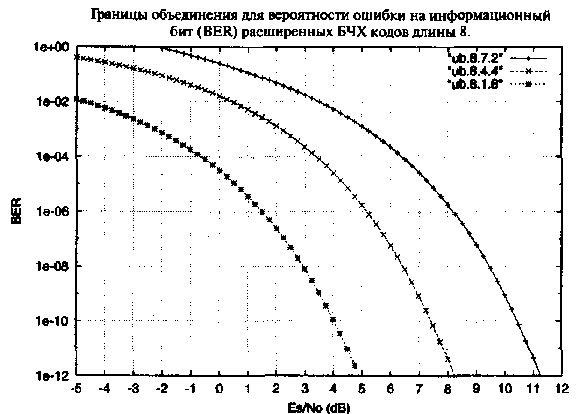
Рис. 24. Оценки BER по границе объединения для расширенных БЧХ кодов длины 8. Двоичный канал с АБГШ.

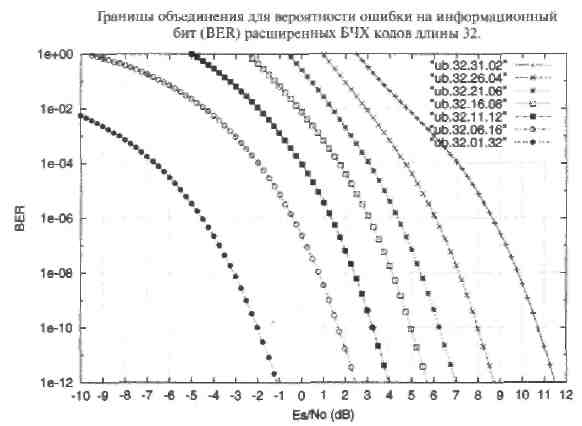
Рис. 25. Оценки BER по границе объединения для расширенных БЧХ кодов длины 32. Двоичный канал с АБГШ.

Рис. 26. Оценки BER по границе объединения для расширенных БЧХ кодов длины 16. Двоичный канал с АБГШ.

Рис. 27. Оценки BER по границе объединения для расширенных БЧХ кодов длины 64. Двоичный канал с АБГШ.

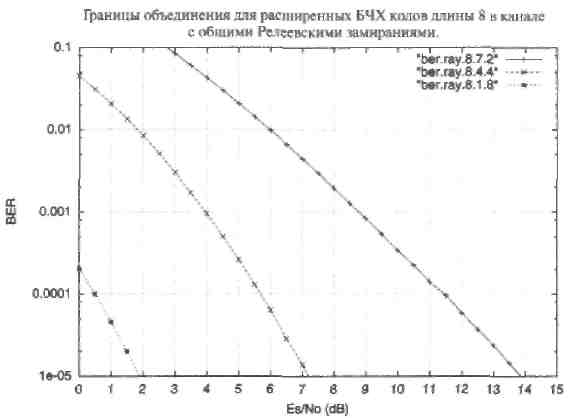
Рис. 28. Оценки BER по границе объединения для расширенных БЧХ кодов длины 8. Двоичный канал с общими Релеевскими замираниями.

Главный вывод этого раздела состоит в следующем. Прежде чем выбирать конкретный алгоритм мягкого декодирования имеет смысл использовать распределение весов кода и границу объединения для предварительной оценки эффективности, достижимой в заданном канале. Для каналов с АБГШ и Релеевскими замираниями граница объединения дает точный ответ для вероятности ошибки на бит менее 10^-4.

Вопросы для самоконтроля

1. Какие коды называются СRС кодами?

2. Какой порождающий многочлен у кода СRС-12?

3. Какой порождающий многочлен у кода СRС-16?

4. Какой порождающий многочлен у кода СRС-CCITT?

5. Какой порождающий многочлен у кода СRС-32?

6. Когда линейный блоковый код является циклическим?

7. Что называют порождающим полиномом g(x) циклического кода?

8. Как найти проверочный полином бинарного циклического кода?

9. Запишите формулу несистематического кодирования двоичного циклического кода.

10. Запишите формулу систематического кодирования двоичного циклического кода.

11. Найдите значение выражения x⁶mod(x³+x+1)?

12. Найдите значение выражения x⁵mod(x³+x+1)?

13. Найдите значение выражения x⁴mod(x³+x+1)?

14. Найдите значение выражения x³mod(x³+x+1)?

15. Как найти неприводимые делители бинома (х^п — 1)?

16. Что такое БЧХ коды?

17. Как найти количество проверочных символов необходимых для коррекции заданного количества ошибок?

18. Что такое граница БЧХ?

19. Из каких блоков состоит архитектура БЧХ декодера?

20. Как лучше рассматривать алгоритм Берлекемпа-Мэсси?

21. Какой алгоритм лежит в основе декодера PGS?

22. Какая процедура лежит в основе алгоритма Евклида?

23. Какое название получил метод поиска корней а(х) на множестве локаторов позиций кодовых символов?

24. Что подразумевается под процессом стирания символа?

25. Можно ли подсчитать распределение весов кода по его дуальному коду.?

26. Оцените, в каких приделах лежит вероятность ошибки на информационный бит BER (если BER = 4) расширенных БЧХ кодов длины 8 при передаче по двоичным каналам с АБГШ.

27. Оцените, в каких приделах лежит вероятность ошибки на информационный бит BER (если BER = 4) расширенных БЧХ кодов длины 32 при передаче по двоичным каналам с АБГШ.

28. Оцените, в каких приделах лежит вероятность ошибки на информационный бит BER (если BER = 4) расширенных БЧХ кодов длины 16 при передаче по двоичным каналам с АБГШ.

29. Оцените, в каких приделах лежит вероятность ошибки на информационный бит BER (если BER = 4) расширенных БЧХ кодов длины 64 при передаче по двоичным каналам с АБГШ.

Дата добавления: 2014-11-29