Пример решения логической задачи

Таблицы истинности для логических выражений

Логические выражения – это удобный метод описания принципа работы логической схемы. Кроме того, часто при проектировании электронных цифровых систем разработчик вначале из условий, решаемой задачи получает ее формальное представление в виде логического выражения. Таблица истинности – это другой точный метод описания того, как работает логическая схема. При работе с цифровыми электронными устройствами надо уметь преобразовывать информацию, представленную в форме таблицы истинности, в логическое выражение. Например, дана таблица истинности, изображенная на рис.30, а. Заметим, что только две из восьми возможных комбинаций двоичных сигналов на входах А, В и С дают на выходе логическую единицу. Эти две возможные комбинации представлены выражениям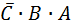и и .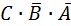

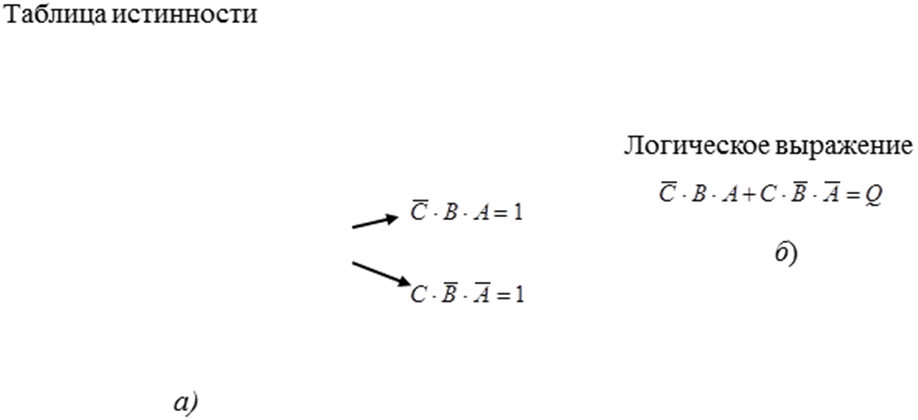
Входы	Выход
С	В	А	Q

Рис.30. Построение логического выражения на основе таблицы истинности

На рис.30, б показано, каким образом эти две комбинации связываются логической функцией ИЛИ, чтобы получить булево выражение для данной таблицы истинности. Как таблица истинности на рис.30, а, так и логическое выражение на рис.30, б показывают принцип действия одной и той же логической схемы.

Часто конструирование логических схем начинается с составления таблицы истинности. Поэтому важно уметь преобразовывать информацию в форме таблицы истинности в логические выражения.

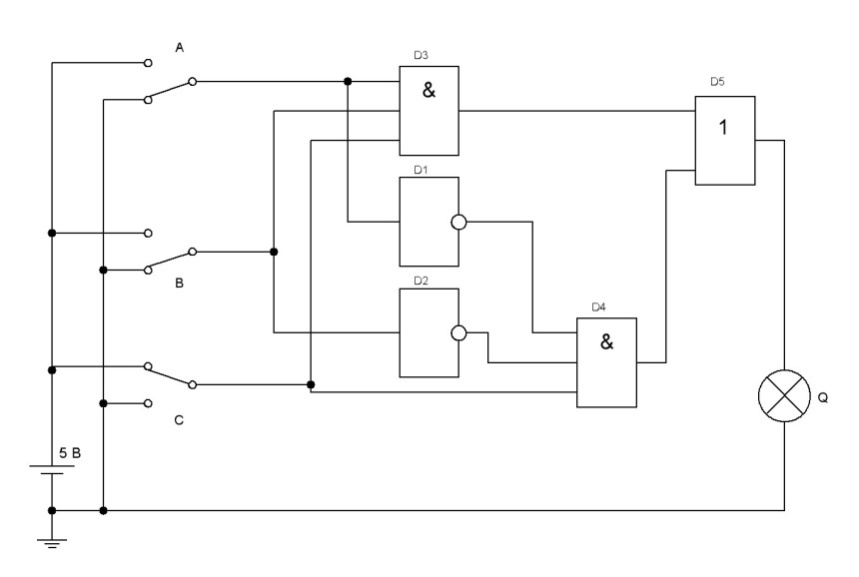
Чтобы зафиксировать навыки выполнения процедур, описанных в разделах 5.1 – 5.3, рассмотрим на примере часто встречающуюся на практике логическую задачу. Предположим, что конструируем простой электронный замок. Замок должен открываться в том случае, когда определенные ключи замкнуты. На рис.31, а приведена таблица истинности для электронного замка. Обратите внимание, что две комбинации входов А, В и С дают на выходе логическую единицу, которая означает, что замок открыт. На рис. 31, б показано, каким образом получается логическое выражение для электронного замка в дизъюнктивной нормальной форме.

а)

Входы	Выход
С	В	А	Q
			1
			в) 0
			1

б)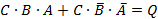

Рис.31. Задача об электронном замке: а – таблица истинности; б – логическое выражение; в – логическая схема

Затем, в соответствии с полученным логическим выражением, составляется логическая схема (рис.31, в). В логической схеме на рис. 31, в для простоты вместо электрического реле механизма замка включена лампочка.

Дата добавления: 2014-11-29