Уравнения характеристик

Классификация УЧП первого порядка

Модельная задача о динамике дорожного движения

Модельная задача о просачивании воды сквозь песок

Модельная задача о травлении материала (химическом, ионно-лучевом, электронно-лучевом, реактивно-ионном)

Модельная задача о процессе изотермической сорбции газа

Модельная задача о химической реакции, протекающей в потоке в режиме идеального вытеснения

Модельная задача о сбросе токсичного вещества в реку

Модельные задачи, приводящие к уравнениям с частными производными первого порядка

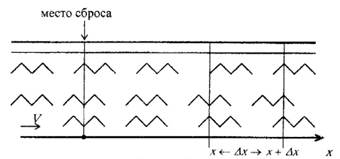
Рисунок 1

Пусть - скорость течения реки. Направим ось вдоль русла реки. Обозначим через расстояние вниз по течению от места сброса вещества. Считаем, что вещество не диффундирует в воде, а переносится течением. Загрязнение реки (концентрация токсичного вещества в воде) будет сначала равно нулю, а затем, поддерживаемое постоянным в точке будет смещаться вниз по течению со скоростью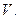

Обозначим через 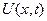концентрацию вещества в точке 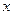в момент времени 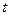. Покажем, что в условиях конвективного переноса, концентрация вещества 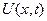удовлетворяет так называемому уравнению переноса:

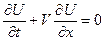. (1)

Выделим в русле реки элементарный участок длины 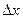, ограниченный сечениями в точках 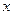и 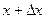. Обозначив площадь любого произвольного сечения через 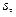объем этого элементарного участка можно приближенно считать равным 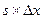или 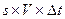. Здесь 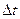- время от момента 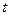до 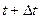, за которое течение со скоростью 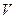переносит вещество на расстояние .

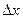Составим уравнение материального баланса (УМБ) для этого участка реки за время от 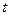до .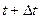

УМБ, выражающее закон сохранения вещества, в текстовом виде схематично можно записать так:

Или:

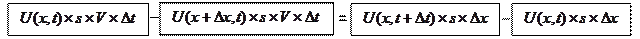
Разделив почленно обе части УМБ на 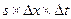, получим:

Совершив предельный переход пр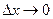и и 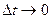, получим уравнение (1):

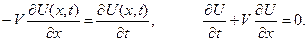
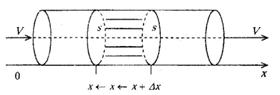
Рисунок 2

Рассмотрим необратимую химическую реакцию первого порядка 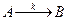, протекающую в одномерном потоке (в реакционной трубке) в режиме идеального вытеснения. Здесь - константа скорости реакции задана; скорость потока считаем равной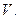

Направим ось 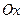вдоль трубки (рис. 2). Пусть 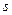- площадь ее поперечного сечения. При описании такого химического процесса необходимо учитывать не только протекание реакции во времени, но и перемещение вещества вдоль пространственной координаты. Поэтому модельное уравнение динамики этого процесса содержит две независимые переменные: координату 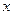и время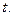

Обозначим через:

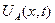концентрацию в точке 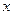в момент времени 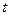непрореагировавшего вещества ,

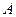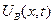концентрацию в точке 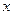в момент времени 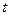образовавшегося вещества 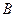(прореагировавшего вещества А). Покажем, что динамика процесса моделируется уравнением химической кинетики:

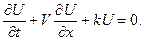(2)

Выделим в реакционной трубке (в потоке) элементарный участок длины 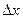, ограниченный сечениями в точках 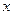и 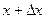; его объем - 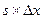или .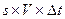

Составим уравнение материального баланса (УМБ) для этого элементарного участка за время от 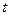до .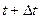

УМБ выражает закон сохранения вещества.

УМБ в текстовом виде схематично можно представить так:

или в формализованном виде:

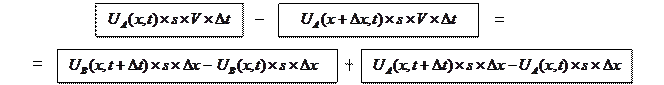
Разделив почленно обе части УМБ на 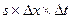, получим:

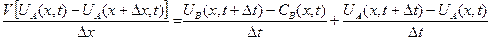
Совершив предельный переход пр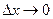и и 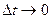, приходим к уравнению:

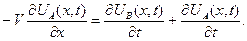
Физический смысл 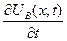- истинная скорость химической реакции первого порядка, которая равна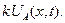

Окончательно УМБ принимает вид (2):

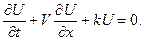
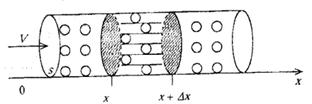
Рисунок 3

Пусть через трубку с постоянной площадью поперечного сечения 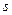, заполненную адсорбентом (поглощающим пористым веществом) пропускается газовоздушная смесь – ОВ (отравляющее вещество).

Тепловыделения в трубке бесконечно малы, а температуры потока и адсорбента одинаковы.

Считаем, что скорость потока 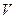велика, и процесс диффузии не играет существенной роли в переносе ОВ.

Направим ось 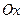вдоль трубки (рис. 3).

Обозначим через:

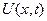концентрацию адсорбтива, то есть ОВ, находящегося в газовой фазе, в точке х в момент времени ,

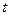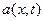концентрацию адсорбата, то есть ОВ, в адсорбированной фазе, в точке х в момент времени .

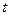Покажем, что концентрация ОВ удовлетворяет уравнению изотермической сорбции газа:

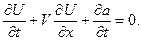
Рассмотрим элементарный слой адсорбента, заключенный между сечениями трубк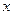и и .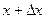

Составим уравнение материального баланса (УМБ) для этого элементарного слоя за время от 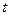до .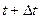

УМБ в текстовом виде схематично можно записать так

или в формализованном виде:

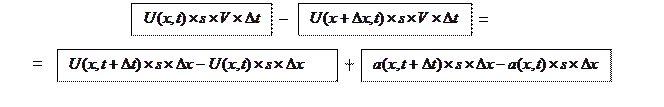
Используя равенство 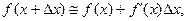левую часть УМБ можно преобразовать следующим образом:

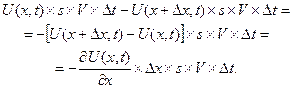
Аналогично правую часть представим так:

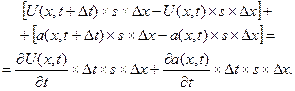
Итак,

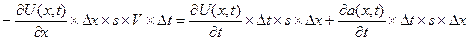
Отсюда, разделив почленно обе части УМБ на 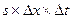, получим:

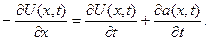
И, наконец, приходим к уравнению (3):

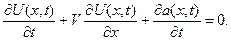
Если известна основная кинетическая зависимость 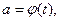где 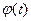- гладкая функция, то уравнение (3) примет вид:

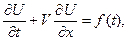(4)

где .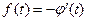

Если к УМБ присоединить уравнение кинетики сорбции (изотермы сорбции)

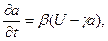
где 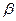- кинетический коэффициент,

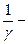коэффициент Генри, 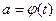- непрерывная, не обязательно гладкая функция, то уравнение (3) примет вид:

(5)

где .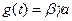

В начальный момент времени имеется некоторый профиль травимого материала. Вследствие процесса травления каждый участок профиля движется в направлении нормали с некоторой скоростью 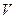. Выведем уравнение эволюции профиля для двухмерного случая.

На рисунке 4 показаны профили для двух моментов времен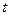и: и .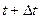

Рисунок 4

Функция описывающая форму профиля, зависит от двух переменных: координаты х и времени .

За время 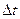точка А профиля смещается в направлении нормали, на расстояние , которое мало.

Смещение точки А по вертикали за время 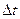также мало:

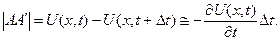
В силу малости 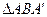можно считать прямоугольным.

Из прямоугольного :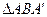

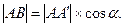(6)

Угловой коэффициент касательной АМ к исходному профилю травимого материала, задаваемого функцией 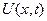в точке А, равен:

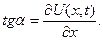(7)

Поскольку 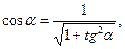то учитывая (7),

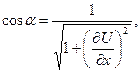
Подставляя в равенство (6) выражения для 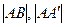и , получим

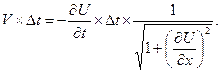
Разделив обе части последнего равенства на 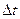, приходим к искомому уравнению травления материала:

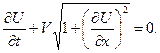(8)

Многообразие процессов, описываемых этим уравнением, связано с различным видом функции V, которая может зависеть от 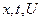и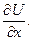

В модельных задачах 3 и 4, используя приближенные равенства, мы позволили небезупречный с точки зрения математической строгости переход от уравнений материального баланса (УМБ) к уравнениям в частных производных. Однако при моделировании физико-химических процессов такой нестрогий подход вполне приемлем, поскольку приводит к простым практически полезным моделям.

Математическая строгость изложения приводит к более сложным выкладкам на основе использования понятия и свойств определенного интеграла. Проиллюстрируем это на следующих модельных задачах.

Пусть вода просачивается через песок сверху вниз. Направим ось 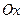вниз. Через 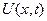обозначим плотность воды в песке в точке х в момент времени 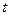. Скорость движения воды 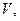очевидно, зависит от ее плотности, то есть 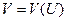, где 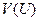есть заданная функция, причем 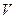возрастает вместе с .

Рассмотрим баланс воды в слое 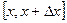. За время 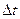изменение количества воды равно

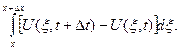
Это изменение происходит за счет разности входящего потока

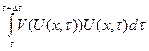
и выходящего потока

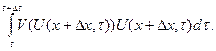
Таким образом получаем УМБ:

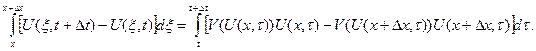
Предполагая наличие непрерывных частных производных у функции 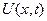и дифференцируемость сложной функции 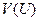, применим теорему о конечном приращении:

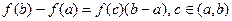
и. теорему о среднем для определенного интеграла

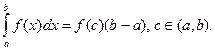
Получим, преобразуя левую и правую части УМБ,

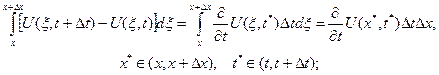
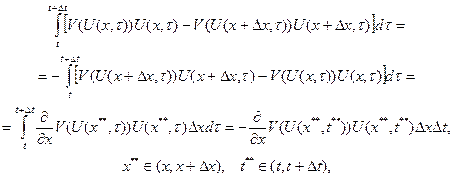
то есть

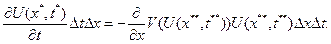
Разделив последнее равенство на 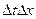и устремив 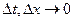, в силу непрерывности всех членов соотношения получим уравнение

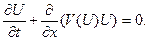
Используя правило дифференцирования произведения, один из множителей которого является сложной функцией, получим

где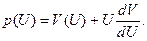

И окончательно,

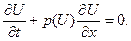(9)

Типичными задачами для уравнения (9) являются как с заданным начальным условием:

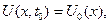(10)

так с граничным условием:

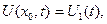(11)

то есть задается (11) - плотность воды либо на границе слоя песка на все моменты времени, либо (10) - на всей глубине просачивания в начальный (фиксированный) момент времени.

В отличие от уравнений в частных производных первого порядка (1), (2), (3), называемых линейными, в которых как частные производные искомой функции, так и сама неизвестная функция входят линейно с постоянными коэффициентами, в уравнении (9) коэффициент 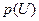при частной производной по х зависит от неизвестной функции. В силу этого обстоятельства уравнение (9) называется квазилинейным. Уравнение (8) из модельной задачи 4 не относится ни к линейным, ни к квазилинейным уравнениям, а является нелинейным, так как в нем присутствует квадрат частной производной, который входит в подкоренное выражение.

Предположим, что автомобили движутся слева направо по скоростной автостраде, у которой нет боковых въездов и съездов.

Направим ось 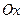вдоль дороги. Обозначим через 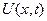плотность автомобилей в точке х в момент времени 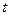- число авто, находящихся на расстоянии х от начала автострады в момент времени .

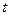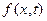потокавтомобилей в точке х - число авто, проезжающих в единицу времени через поперечное сечение дороги в точке х.

Покажем, что они удовлетворяют уравнению:

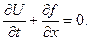(12)

Составим УМБ, выражающий закон сохранения числа автомобилей для участка дороги .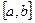

С одной стороны, изменение числа автомобилей за единицу времени на 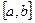равно

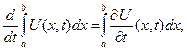
с другой стороны, применяя формулу Ньютона-Лейбница, -

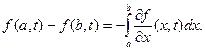
Приравнивая эти два интеграла, получаем

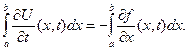
Поскольку промежуток 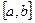произволен, подынтегральные функции равны, то есть приходим к уравнению (12).

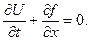
В задачах дорожного движения пользуются экспериментально найденной зависимостью потока автомобилей от плотности: 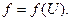В этом случае по правилу дифференцирования сложной функции

.

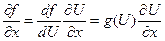Значит (12) можно переписать следующим образом:

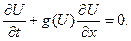
Пусть, например, зависимость потока от плотности квадратичная, то есть .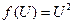

Тогда уравнение (12) принимает вид:

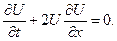(13)

В динамике жидкости величина 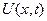может обозначать плотность жидкости в точке, а 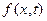- поток жидкости.

Квазилинейными уравнениями с частными производными первого порядка называются уравнения вида:

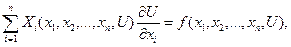
где 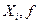- известные функции,

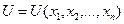- функция, подлежащая определению.

Если функции от не зависят, то уравнение с частными производными называется линейным; если функция то УЧП называется однородным.

Типология УЧП первого порядка

Таблица 1

Модельная задача	Название УЧП	Вид УЧП первого 1-го порядка	Тип УЧП первого порядка
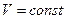
О сбросе токсичного вещества в реку	уравнение конвективного переноса		линейное однородное с постоянными коэффициентами
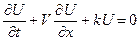
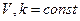
О химической реакции, протекающей в потоке в режиме идеального вытеснения	уравнение химической кинетики		квазилинейное неоднородное с постоянными коэффициентами
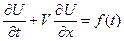
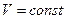
О процессе изотермической сорбции газа	уравнение сорбции		линейное неоднородное
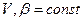
уравнение изотермической сорбции		квазилинейное
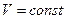
О травлении материала (химическом, ионно-лучевом, электронно-лучевом, реактивно-ионном)	уравнение травления материала		нелинейное
О просачивании воды сквозь песок	кинетическое уравнение		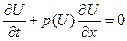квазилинейное однородное
О динамике дорожного движения	кинетическое уравнение		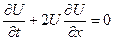квазилинейное однородное

Рассмотрим оператор

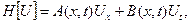(14)

где 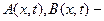заданные непрерывные функции, определенные в некоторой области ;

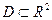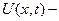непрерывно дифференцируемая функция в этой области 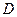, причем

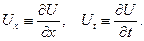
Как известно, производная функции 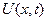в фиксированной точке 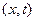по направлению единичного вектор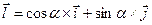а равна

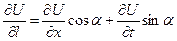
Выражение

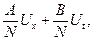
где 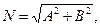можно интерпретировать как производную функции 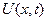в точке 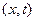по направлению единичного вектора с компонентами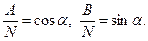

Ясно, что

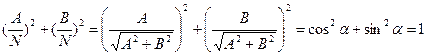
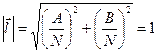
Тога оператор 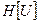, задаваемый формулой (14) можно представить в следующем виде

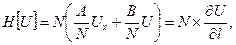
и рассматривать как производную от функции 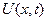по направлению вектора умноженную на

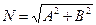
Определение 1. Направление, задаваемое вектором называется характеристическим направлением оператора 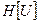в фиксированной точке .

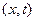Определение 2. Кривая , в каждой точке которой ее касательная имеет характеристическое направление оператора 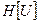, называется характеристикой оператора .

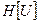Рисунок 5. Характеристика оператора

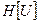
В каждой точке 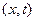характеристики вектор 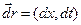коллинеарен вектору что означает пропорциональность координат этих векторов:

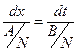
Таким образом, приходим к обыкновенному дифференциальному уравнению характеристик

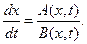или (16)

Введя параметр 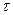, меняющийся вдоль характеристики, можно записать

,

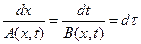откуда получаем эквивалентную (16) систему ОДУ в нормальном виде:

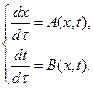(17)

Решив обыкновенное дифференциальное уравнение (16) или нормальную систему обыкновенных дифференциальных уравнений (17), можно найти и построить характеристики везде в той части пространства, где определена дифференцируемая функция 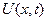, иначе - где задано плоское скалярное поле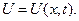

Пример 1. Для оператора 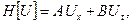где 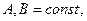дифференциальное уравнение характеристик (16) имеет вид

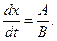
Разделяя переменные и интегрируя уравнение, получаем

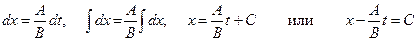
Следовательно, характеристики данного оператора 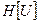представляют собой однопараметрическое семейство параллельных прямых с угловым коэффициентом 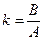, заполняющих собой всю плоскость .

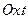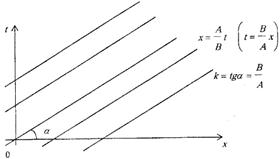
Рисунок 6. Характеристики оператора 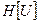образуют однопараметрическое

семейство прямых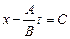

Применим понятие характеристик к изучению уравнений в частных производных (УЧП) 1-го порядка вида

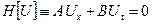(18)

Определение 3. Характеристиками УЧП 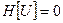называются характеристики оператора .

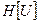Теорема. Если функция 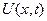удовлетворяет уравнению (18), то есть 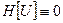то на каждой характеристике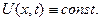

Действительно, принимая во внимание (18), вдоль каждой характеристики имеем

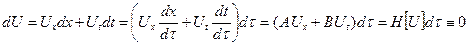
Итак,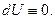

Отсюда следует, что на каждой характеристике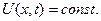

Дата добавления: 2014-11-29