Физическая интерпретация полученного решения

Задача Коши. Метод характеристик

Физическая интерпретация этого факта

Если 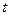- время, то начальное состояние 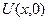распространяется по характеристикам. Чтобы найти 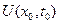в произвольной фиксированной точке 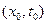, надо через эту точку провести характеристику, найти ее точку пересечения с осью 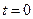. Пусть это будет точк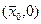а тогда 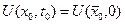.(рисунок 6)

Рисунок 7

Пример 2. На рисунке 6 вдоль каждой характеристики – прямой 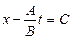функция 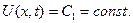При этом 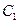имеет разные значения вдоль различных характеристик, то есть или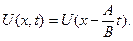

Пример 3. Найдем характеристики УЧП 1-го порядка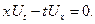

Дифференциальное уравнение характеристик имеет вид

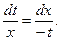
Разделяя переменные и интегрируя ОДУ получим

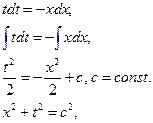
Следовательно, характеристики УЧП представляют собой однопараметрическое семейство окружностей, радиуса , заполняющих собой всю плоскость .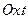

Задача Коши состоит в отыскании решения УЧП, если известно начальное отклонение .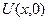

Рассмотрим задачу Коши для уравнения переноса

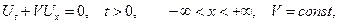(19)

с начальным условием

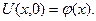(20)

Дифференциальное уравнение характеристик имеет вид

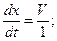
интегрируя его, получаем

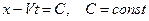
Вдоль каждой характеристики 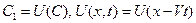- произвольная дифференцируемая функция.

Учитывая начальное условие (20), записываем решение задачи Коши (19)-(20):

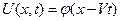
Функция 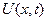называется отклонением в точке 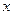в момент времени 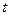. Рассмотрим точку 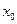. Допустим, далее, что из этой точки в положительном направлении оси 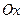в момент времени 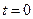начинает двигаться наблюдатель со скоростью V. В момент времени 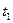он окажется в точке 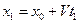. Величина отклонения, которую наблюдатель будет видеть в точке 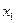в момент времени 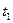, будет равна 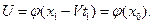Таким образом, наблюдатель в любой момент времени будет видеть в точке, где он находится, одну и ту же величину отклонения, равную 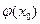.Следовательно, начальный профиль 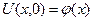будет двигаться со скоростью 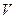в положительном направлении оси 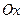, как жесткая система, не изменяя формы (рис.8).

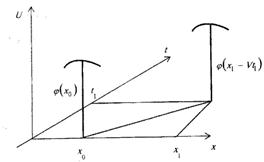
Рисунок 8

Пример 4. Решение задачи Коши для уравнения переноса (6) с начальным условием

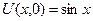
имеет вид

.

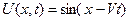Пример 5. Уравнение химической кинетики

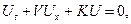где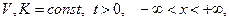

а) привести к виду

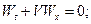
б) решить задачу Коши при начальном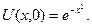

а) Выполним подстановку вида

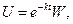где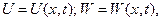

в данное УЧП.

Так как

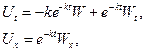
то

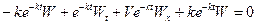
Домножив почленно на 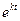обе части последнего уравнения, получим

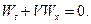
б) Решение полученного УЧП вдоль каждой характеристики 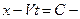это произвольная дифференцируемая функция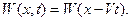

Из начального условия

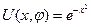
и подстановки

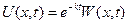
следует

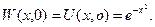
Таким образом, решение промежуточной задачи Коши:

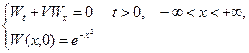
имеет вид:

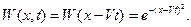
И, наконец, решение задачи Коши для исходного УЧП:

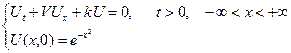
следует из полученной формулы выполнением подстановки

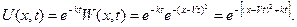
Пример 6. Решить задачу Коши для УЧП 1-го порядка из примера 3:

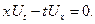
Вдоль каждой характеристики данного УЧП- окружности 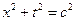решение этого УЧП – произвольная дифференцируемая функция 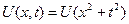. Исходя из заданного вида начального профиля получаем следующее отклонение в точке 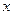в момент времени :

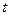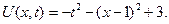
Дата добавления: 2014-11-29