Задачи для самостоятельного решения. Задача Коши. Метод вариации произвольной постоянной

Задача Коши. Метод вариации произвольной постоянной

Рассмотрим решение задачи Коши для линейного неоднородного уравнения в частных производных 1-го порядка с постоянными коэффициентами:

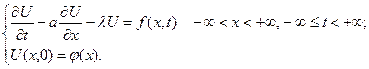(21)

УЧП можно интерпретировать, например, как уравнение конвективного переноса токсичного вещества в потоке, сопровождаемого химической реакцией 1-го порядка (или рассеиванием), при наличии источников вещества заданной интенсивности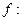

где - скорость изменения концентрации

- плотность потока

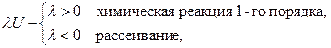
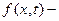интенсивность источника вещества,

при условии, которые с физической точки зрения означают, что длина потока много больше его диаметра.

Приведем решение УЧП общего вида из задачи Коши (20):

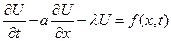
Введем новые переменные: а именно

(22)

Тогда

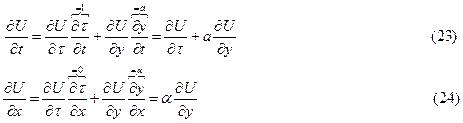
Из (22) следует

Учитывая (23) и (24), получим

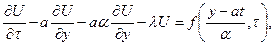
или

При имеем то есть за координатную линию 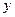берется характеристика дифференциального оператора

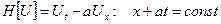
И далее,

Решим однородное УЧП:

Получим

Полагаем тогда

Отсюда

Интегрируем последнее уравнение:

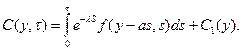
Возвращаемся к искомой функции и исходным переменным:

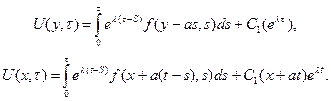
Для определения 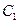используем начальное условие

И, наконец,

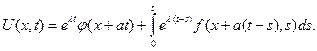(25)

Пример 7. Используем полученное решение задачи Коши (25) для уравнения (5) изотермической сорбции. Запишем аналитическое решение модельной задачи 3.

Пусть

тогда по формуле (25)

Пример 8. Решить задачу коши

Запишем аналитическое решение данной задачи по формуле (25) при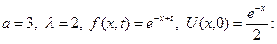

Задание 1

Решить методом характеристик задачу Коши для линейного однородного УЧП 1-го порядка

1.1.

1.2.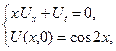

1.3.

1.4.

1.5.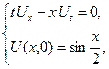

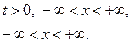
1.6.

1.7.

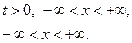
1.8.

1.9.

1.10.

1.11.

1.12.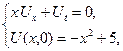

1.13.

1.14.

1.15.

1.16.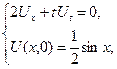

1.17.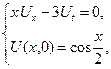

1.18.

1.19.

1.20.

1.21.

1.22.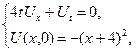

1.23.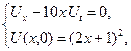

1.24.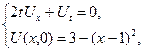

1.25.

Задание 2

Решить задачу коши, предварительно преобразовав квазилинейное УЧП 1-го порядка к линейному уравнению переноса:

2.1.

2.2.

2.3.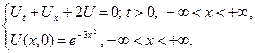

2.4.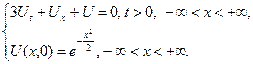

2.5.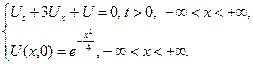

2.6.

2.7.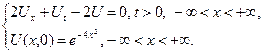

2.8.

2.9.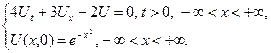

2.10.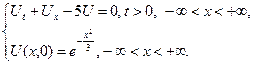

2.11.

2.12.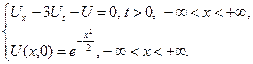

2.13.

2.14.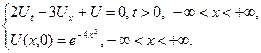

2.15.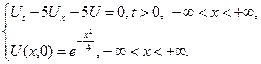

2.16.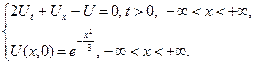

2.17.

2.18.

2.19.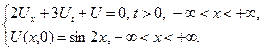

2.20.

2.21.

2.22.

2.23.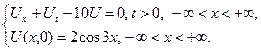

2.24.

2.25.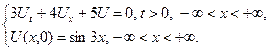

Задание 3

Решить методом вариации произвольной постоянной задачу Коши для неоднородного УЧП 1-го порядка:

3.1.

3.2.

3.3.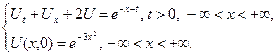

3.4.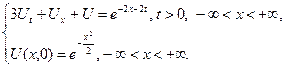

3.5.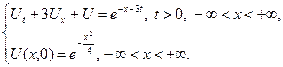

3.6.

3.7.

3.8.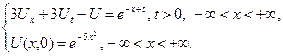

3.9.

3.10.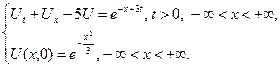

3.11.

3.12.

3.13.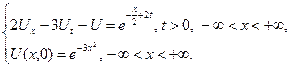

3.14.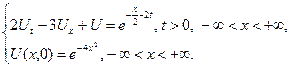

3.15.

3.16.

3.17.

3.18.

3.19.

3.20.

3.21.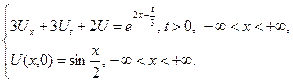

3.22.

3.23.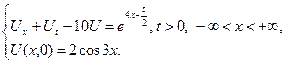

3.24.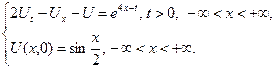

3.25.

Рекомендуемая литература

1. Жукова Г.С. Обыкновенные дифференциальные уравнения.- М.: Изд-во МГСУ, 2003 – 504с.

2. Лаптев Г.И., Лаптева Н.А., Володин Ю.В. Дополнительные главы математического анализа: Учебное пособие. – М.: ACADEMIA АПКиППРО, 2008. – 90с.

3. Лаптев Г.И., Лаптева Г.Г. Линейные и нелинейные уравнения математической физики. – М.: Изд-во РХТУ им. Д.И. Менделеева, 2003. – 329 с.

4. Орлик Л.К., Кармишин А.М., Мудракова О.А. Уравнения математической физики. Метод характеристик. – М.: Изд-во ВАРХБЗ, 2004. – 50с.

5. Кармишин А.М., Орлик Л.К. Теория поля в примерах и прикладных задачах. – М.: Изд-во ВУРХБЗ, 2003.- 96 с. (Орлик Л.К. Электронный вариант, 2005 г.)

Дата добавления: 2014-11-29