Определитель матрицы

Пусть дана квадратная матрица второго порядка:

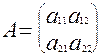
Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число: .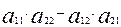

Определитель второго порядка записывается так:

D=detА=

Определитель второго порядка равен разности попарных произведений элементов главной и побочной диагоналей.

Примеры:

Вычислить определители второго порядка:

а) 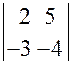; б)

Решение:

а) =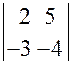

б) =

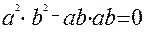
Определителем (или детерминантом) третьего порядка, соответствующим данной матрице, называется число: а₁₁а₂₂а₃₃+а₂₁а₃₂а₁₃+a₁₂a₂₃а₃₁-а₁₃а₂₂а₃₁-а₁₂а₂₁а₃₃-а₁₁а₂₃а₃₂

Пример:

Вычислить определитель третьего порядка: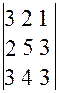

Решение:

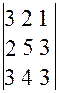
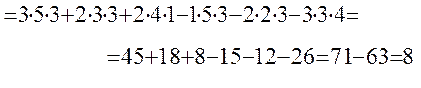
Основные свойства определителей

1. Определитель не измениться, если его строки поменять местами с соответствующими столбцами (т.е. транспонировать).

Например:

Это свойство называют свойством равноправности строк и столбцов.

2. При перестановке двух строк (или столбцов) определитель изменит свой знак на противоположный:

Например:

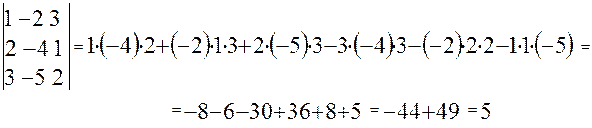
Поменяв местами первый и второй столбцы, получим:

3. Общий множитель всех элементов строки (или столбца) можно вынести за знак определителя:

Например:

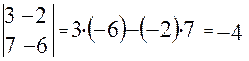
Если множитель (-2) вынести за знак определителя, то получим:

4. Определитель с двумя одинаковыми строками или столбцами равен нулю.

Например:

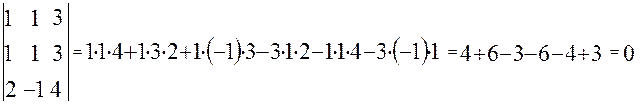
Из свойств 3 и 4 вытекает следующее свойство:

5. Если все элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.

Например:

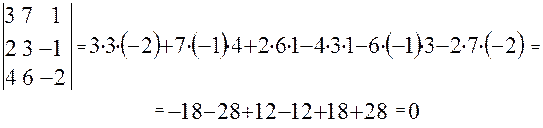
6. Если к какой-либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменит своей величины.

7. Треугольный определитель, у которого все элементы, лежащие выше (или ниже) главной диагонали, - нули, равен произведению элементов главной диагонали:

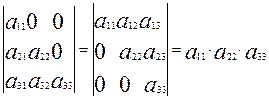
Миноры и алгебраические дополнения

Минором М _ij элемента а_ij определителя D называется такой новый определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащих данный элемент.

Например, минор М₁₂, соответствующий элементу а ₁₂ определяется:

Получается, если вычеркнуть из определителя D первую строку и второй столбец, т.е.

М₁₂

Пример:

Записать М₁₁; М₂₁; М₂₃; М₃₂ определителя:

Решение:

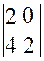М₁₁ ; М₂₁= ; М₂₃= 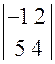; М₃₂=

Алгебраическим дополнением элемента а_ij определителя D называется минор М_ij этого элемента, взятый со знаком (-1)^i+j

Алгебраическое дополнение элемента а_ij принято обозначать А_ij.

Таким образом, А_ij=(-1)^i+j М_ij

Пример:

Найти алгебраические дополнения элементов а ₁₃, а ₂₁, а ₃₁ определителя

Решение:

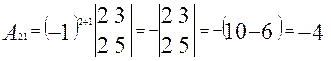
Теорема о разложении определителя по элементам строки или столбца.

Сумма произведений элементов любой строки (или столбца) определителя D на их алгебраические дополнения равна этому определителю, т.е.:

D= а _i1А_i1+ а _i2A_i2+…+ а _inА_in

или

D= а _1jА₁j+ а _2jА_2j+…+ а _njА_nj

Эти соотношения называются разложением определителя по элементам i -й строки или j -го столбца.

Если определитель имеет четвертый или более высокий порядок, то его также можно разложить по элементам строки или столбца, а затем понижать порядок алгебраических дополнений.

Перечислим способы вычисления определений:

1. Определитель можно вычислить, используя непосредственно его определение. Этим способом удобно находить определители второго и третьего порядков, а для определителя высокого порядка применим следующий способ.

2. Определитель можно вычислить с помощью его разложения по элементам строки или столбца.

3. Определитель можно вычислить способом приведения к треугольному виду. Этот способ основан на том, что в силу свойства 7 треугольный определитель равен произведению элементов главной диагонали.

Чтобы получить треугольный определитель, нужно, используя свойство 6, к какой-либо строке (или столбцу) заданного определителя прибавлять соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, до тех пор, пока не придем к определению треугольного вида.

Например, вычислить определитель:

Вычитая первую строку из всех остальных, сразу получим определитель треугольного вида:

Примеры:

1. Вычислить определитель:

,

Разложив его: а) по элементам 1-й строки;

б) по элементам 2-го столбца.

Решение:

а)

б)

2. Вычислить определитель:

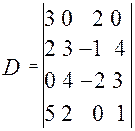
Решение:

Разложим определитель по элементам 1-й строки (так как она содержит два нулевых элемента):

=

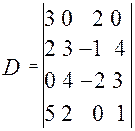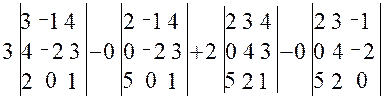
Поскольку второй и четвертый члены разложения равны нулю, имеем:

Дата добавления: 2014-11-29