Понятие функции алгебры логики. Формы представления функций алгебры логики, их преобразования и минимизация

Метод инженерного синтеза цифровых устройств на основе таблиц Хаффмена

2.1 Основные положения [1, 2, 4, 8, 9, 30, 31,32]

В процессе синтеза цифрового устройства необходимо определить шесть его объектов (п. 1.4).

Описываемый метод состоит из двух этапов:

1. Этапа абстрактного синтеза;

2. Этапа структурного синтеза.

Этот метод называют еще каноническим методом синтеза цифровых автоматов (от слова «канон» - основа, закон, база).

На этапе абстрактного синтеза на основе словесно сформулированных условий работы устройства определяется закон его функционирования с записью на одном из формализованных языков: языке таблиц переходов, граф-схем алгоритмов, логических схем алгоритмов и других. Наиболее широко используемым из них являются язык таблиц переходов, обладающий наибольшей универсальностью, и язык граф-схем алгоритмов, особенно эффективный при синтезе устройств управления при микропрограммном принципе реализации цифровых устройств и, в частности, процессоров вычислительных устройств. [3,4,9,11,15]

На этом этапе определяются входы и выходы устройства и комбинации их состояний, производится минимизация числа внутренних состояний устройства и определяется число элементов памяти, необходимое для его построения. То есть после составления таблицы переходов на этапе абстрактного синтеза определяются четыре объекта цифрового устройства: множество состояний входов, множество состояний выходов, множество внутренних состояний, начальное внутреннее состояние.

На этапе структурного синтеза строится комбинационная схема с учетом выбранных элементов памяти, то есть отыскиваются функции переходов и функции выходов, являющиеся функциями алгебры логики, описывающими цепи комбинационной схемы (определяются еще два объекта цифрового устройства).

Далее выбирают функционально полную систему логических элементов (базис) и тип элементов памяти (объяснение этих терминов будет приведено ниже).

Этап структурного синтеза заканчивается построением схемы цифрового устройства, состоящей из логических элементов и элементов памяти.

Таким образом, синтез устройства заключается по существу в определении шести объектов цифрового устройства. Более подробно методика синтеза будет представлена ниже, в том числе на примерах.

Далее будут рассматриваться асинхронные цифровые устройства потенциального типа, так как переход к синхронным устройствам не вызывает никаких дополнительных трудностей и даже наоборот – снимает проблему устранения состязаний, а также потому, что в микросхемотехнике практически всегда используются цифровые устройства с потенциальными связями.

2.2 Использование аппарата алгебры логики при разработке и описании цифровых устройств [1,3,5,10,22]

Как уже сказано цепи, воздействующие на элементы памяти цифрового устройства и его внешние выходы, описываются соответственно функциями переходов и функциями выходов, являющимися функциями алгебры логики, которые получаются и оптимизируются с использованием аппарата алгебры логики. Это цепи, которые образуют логический преобразователь (комбинационную схему) цифрового устройства в соответствии с рис. 1.2

Аппарат алгебры логики является одной из составных частей математической логики. Алгебру логики называют также по имени английского математика Джорджа Буля, разработавшего в конце девятнадцатого века её основные положения, булевой алгеброй (алгеброй Буля).

Строгие доказательства применимости булевой алгебры к исследованию и оптимизации структуры релейно-контактных схем дали в конце 30-х годов двадцатого века советский ученый В. И. Шестаков, американский математик К.Шеннон и японский ученый А. Накашима.

Эти принципы были в дальнейшем распространены на устройства переработки информации на другой элементной базе.

Синтез цифрового устройства в целом в соответствии с рис. 1.2, т.е. синтез последовательностного устройства, производится с применением инженерных методов, основанных на использование методов теории конечных автоматов, разработанных в трудах американца К.Шеннона, советского ученого В.М. Глушкова [8] и многих других.

Функцией алгебры логики (булевой функцией) называют функцию, которая может принимать только два значения 0 и 1 в зависимости от комбинаций значений аргументов, которые также принимают только значения 0 и 1. Говорят, что функция алгебры логики – двоичная функция двоичных аргументов [1,3].

Функции в математике могут задаваться аналитически или в виде таблицы. Табличное задание логических функций называют таблицами истинности. При табличном задании логических функций определяются все возможные комбинации значений аргументов, число которых конечно, и соответствующие им значения функций. То есть табличная запись однозначно определяет логическую функцию в отличии от других функций, в которых количество значений аргументов и функций бесконечно и таблица определяет функцию только в конечном числе точек.

Таблица 2.1 является таблицей истинности функций одного аргумента

Таблица 2.1

Аргумент х	Функция
f0(x)	f1(x)	f2(x)	f3(x)

Аналитически эти функции представляются выражениями:

f₀(x) = 0 (константа 0);

f₁(x) = 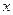; (функция повторяет значение аргумента);

f₂(x) = (функция принимает значение противоположное значение аргумента, что обозначается черточкой над аргументом; операцию называют операцией отрицания или инверсией, или логическим «НЕ»);

f₃ (x) = 1 (константа 1).

В реальных устройствах функция f₀(x) представляет собой соединение соответствующего ей выхода с общей точкой схемы (соединение с нулевым потенциалом); f₁(x) – соединение выхода со входом; f₃(x) – соединение выхода с источником постоянного напряжения, потенциал которого соответствует логической единице; f₂(x) реализуется различного рода элементарными схемами [3,5].

Элемент, выполняющий инверсию, изображается на схемах в соответствии с рис. 2.1 а

Количество комбинаций значений аргументов функций от «n» аргументов равно 2ⁿ. При n = 1 таблица истинности содержит две строки 2¹ = 2 – таблица 2.1; при n = 2 таблица истинности содержит четыре строки 2² = 4 – таблица 2.2.

При этом количество функций, зависящих от «n» аргументов будет 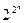. То есть для одной переменной это 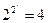– таблица 2.1, а для двух переменных 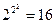- таблица 2.2.

Таблица 2.2

Аргументы

Функции

Х1

Х2

f0

f1

f2

f3

f4

f5

f6

f7

f8

f9

f10

f11

f12

f13

f14

f15

Рис. 2.1

Рис.2.1

Функции f₀(x₁х₂) и f₁₅(x₁х₂) являются соответственно константами нуля и константами единицы.

Рассмотрим функции из таблицы 2.2, применяемые при синтезе цифровых устройств, варианты их названий и аналитические выражения, а также изображение на схемах элемента, реализующего функцию.

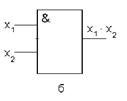
f₁(x₁х₂): название – конъюнкция или логическое «И», или логическое произведение; аналитическое выражение - x₁х₂ или x₁&х₂, или x₁Λх₂; обозначение соответствующего элемента на рис. 2.1 б;

f₇(x₁х₂): название – дизъюнкция или логическое «ИЛИ», или логическая сумма; аналитическое выражение - x₁+ х₂ или ; обозначение соответствующего элемента на схеме на рис. 2.1 в;

f₁₄(x₁х₂): название – логическое «И-НЕ» или штрих Шеффера, или отрицание конъюнкции; аналитическое выражение - x₁│х₂, или через операции конъюнкция и инверсия ; обозначение соответствующего элемента на рис. 2.1 г.;

f₈(x₁х₂): название – логическое «ИЛИ-НЕ» или стрелка Пирса, или функция Вебба, или отрицание дизъюнкции; аналитическое выражение - x₁↓х₂ или через дизъюнкцию и инверсию ; обозначение соответствующего элемента на рис. 2.1 д;

f₆(x₁х₂): название – неравнозначность или сумма по модулю два, или исключающее «ИЛИ»; аналитическое выражение - или через конъюнкцию, дизъюнкцию и отрицание ; обозначение соответствующего элемента на рис. 2.1 е (название сумма по модулю два происходит от того, что функция равна единице, когда сумма двух аргументов равна единице);

f₉(x₁х₂): название - равнозначность или эквивалентность; аналитическое выражение x₁ 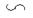х₂ или , или x₁ ↔ х₂, или через операцию конъюнкция, дизъюнкцию и отрицание - ; обозначение соответствующего элемента на рис. 2.1 ж.

Описание физической реализации рассмотренных функций (схемы логических элементов) можно найти, например в [1,2, 3, 5, 6, 22].

Логические функции, перечисленные выше, при большем количестве переменных строятся по таким же правилам, как и функции двух переменных, т.е. конъюнкция равна единице, когда все аргументы равны единице, а в остальных случаях равна нулю. Дизъюнкция равна единице, когда хотя бы один из аргументов равен единице и т.д.

Переход от табличной записи логических функций к их аналитической записи осуществляется путем составления совершенной дизъюнктивной нормальной формы (СДНФ) или совершенной конъюнктивной нормальной формы (СКНФ) [1,2,3,5].

Эти формы содержат максимальное число переменных. От них как правило нецелесообразно переходить к схеме. Поэтому производится их минимизация. При этом преимущественно пользуется СДНФ. В результате получается минимальная дизъюнктивная нормальная форма (МДНФ), которая содержит минимальное количество элементов (букв и конъюнкций).

В процессе минимизации получают сначала минимальные конъюнкции (простые импликанты), затем определяют различные комбинации импликант, дизъюнкция которых в данной комбинации удовлетворяет табличной записи функции (получают тупиковые формы). Далее из тупиковых форм выбирается содержащая минимальное число букв и импликант - МДНФ. При определении тупиковых форм используется импликантная матрица и метод (алгоритм) Петрика. [1,3,5,17].

Преобразование аналитических выражений производится с использованием тождеств и законов алгебры логики. При нахождении простых импликант используются методы карт Карно или диаграмм Вейча. Более универсальным является метод Квайна-Мак-Класки.

Эти методы основаны на операции «склеивания» [1,3,5]. Переход от дизъюнктивной нормальной формы или конънктивной нормальной формы к форме, использующей функции отрицания дизъюнкции, отрицание конъюнкции («ИЛИ-НЕ», «И-НЕ»), осуществляется с использованием формул (закона) де Моргана (принцип двойственности алгебры Буля), [1,3,5].

Все изложенное здесь по поводу преобразований логических функций предназначено для того, чтобы учащийся смог оперативней ориентироваться в литературе, на которую приведены ссылки и где подробно, с доказательствами и примерами приведен этот материал.

Дата добавления: 2014-11-29