Этап абстрактного синтеза

На этом этапе, как уже сказано выше, осуществляется переход от словесного описания функций, выполняемых устройством, к их формализованному описанию на одном из языков.

В дальнейшем будет использовать язык таблиц переходов (таблиц Хаффмена), предложенный в 1954 г. американским ученым Д. Хаффменом, так же как и рассмотренная ранее структурная схема (модель Хаффмена).

Таблица переходов (см. таблицу 2.3) в вершинах столбцов содержит всемозможные комбинации состояний входов устройства.

Каждая строка таблицы переходов соответствует внутреннему состоянию устройства, т.е. определенной комбинации состояний элементов памяти.

В клетках таблицы записаны номера входных (или просто состояний) устройства, состоящие из состояний входов и внутреннего состояния (т.е. комбинации состояний элементов памяти или просто состояния элементов памяти) без учета записей справа вверху над номером, которые обозначают состояние внешних выходов устройства.

Устойчивые состояния обозначены цифрами в скобках, а неустойчивые цифрами без скобок. Каждое неустойчивое состояние ведет к устойчивому состоянию и поэтому имеет такой же номер как устойчивое состояние, к которому оно ведет. Состояние выходов устройства проставляются либо рядом с обозначением состояния, либо справа вверху от обозначения состояния. Внутреннее состояние и состояние выходов образуют выходное состояние. [1,2,4,9,30,31,32].

Таблица переходов, построенная на основе словесного описания закона функционирования, в которой в каждой строке содержится не более чем одно обозначение устойчивого состоянии, называют первичной таблицей переходов. Далее многие строки могут быть совмещены с использованием специальных методов. Эти методы основаны на выявлении и объединении так называемых эквивалентных и псевдоэквивалентных состояний и выявлении и объединении совместимых состояний [1,2,4,9].

Эти методы здесь не рассматриваются исходя из того, что таблица переходов для несложных цифровых устройств может быть составлена с минимальным количеством строк на основе интуиции разработчика.

Минимальное количество строк в таблице обеспечивает в дальнейшем использование минимального количества элементов памяти.

Однако, необходимо отметить, что минимальное количество строк не всегда соответствует оптимальному по заданному критерию устройству. Иногда таблица с большим количеством строк приводит к более рациональному устройству.

Рассмотрим примеры построения таблиц переходов по словесному описанию закона функционирования.

Пример 1. Устройство имеет три входа а₁ а₂ а₃ и два выхода z₁ и z₂. При подаче на входы последовательно во времени 3-х единиц в очередности, соответствующей номерам входов, с паузой или без паузы на выходе z₁ должна появиться единица. При любом отклонении от заданной последовательности подачи единицы на входы на выходе z₂ должна появиться единица.

После появления на выходе z₁ единицы отсутствие сигналов на входах приводит устройство в исходное состояние.

Из описания ясно, что это устройство является декодирующим устройством простого последовательно-параллельного кода, подаваемого на его входы. Комбинации его разрядов последовательно во времени на входах а₁ а₂ а₃ выглядят так: 000, 100, 010, 001 (между каждой из комбинаций допускается комбинация 000). Любая другая смена состояний входов является ложной и приводит к появлению единицы на выходе z₂.

Такого же рода устройство может также выполнять роль простого кодового замка.

Таблица 2.3 является формализованным описанием закона функционирования такого устройства. Важным свойством формализованного описания закона функционирования, в данном случае на языке таблиц переходов, является его однозначность, в то время как словесное описание не всегда однозначно толкуется. Во всех таблицах справа вверху над обозначением состояний проставляются состояния выходов z₁ z₂.

Пример 2. Устройство имеет один вход Т и один выход z. В исходном состоянии на вход устройства подан «0» (Т=0). На вход поступает последовательность нулей и единиц. На выходе z должна формироваться единица, совпадающая с четной единицей на входе.

Таблица 2.4 удовлетворяет этому словесному описанию. Состояние выхода z обозначено справа вверху над устойчивым состоянием.

Пример 3. Необходимо синтезировать Т-триггер, изменяющий состояние выхода на противоположное при смене состояния входа Т с «1» на «0».

Это широко известное устройство. Существуют разные варианты его реализации. Во многих учебниках приводится синтез его схемы с учебными целями. Здесь будет приведена наша версия синтеза. Таблица 2.5 описывает работу Т–триггера.

В завершении этапа абстрактного синтеза осуществляется операция кодирования внутренних состояний устройства. Заключается она в присвоении каждому внутреннему состоянию (строке таблицы) определенной комбинации состояний элементов памяти. При этом при переходе от состояния к состоянию необходимо избежать состязаний элементов памяти, что можно обеспечить, как указывалось выше, путем соседнего кодирования (использование кода Грея), когда соседние комбинации отличаются только одним разрядом (переключается только один элемент памяти).

Минимальное количество элементов памяти определяется при этом по формуле [3, 11]

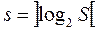, (2.1)

где s – количество элементов памяти; S – количество внутренних состояний, скобки означают, что производится округление до ближайшего большего целого числа, так как число элементов памяти не может быть дробным. В нашем случае для всех трех таблиц переходов: S= 4; s= 2. Если S= 5, то s= 3.

Следует отметить, что минимальное количество элементов памяти далеко не всегда приводит к оптимальному устройству, так как уменьшение числа элементов памяти приводит к усложнению комбинационной схемы и наоборот.

Состояние триггеров (элементов памяти) указаны в графе ЭП, где приведены состояния прямых выходов триггеров Q₁ и Q₂.

На этом этап абстрактного синтеза заканчивается. В результате определены четыре объекта, характеризующие цифровое устройство [п. 1.4]: множество комбинаций состояний входов ρ; множество комбинаций состояний выходов Λ; множество комбинаций состояний элементов памяти Κ, начальное внутреннее состояние æ₀.

Дата добавления: 2014-11-29