Метод аналізу розрахунків

Метод аналізу рахунків (Account Analysis Method) — ме-

[ тод визначення функції витрат шляхом розподілу їх на змін­ні та постійні щодо відповідного чинника на підставі ви­вчення даних рахунків бухгалтерського обліку.

Наприклад, магазин "Час" за звітний період реалізував 2 000 годинників. Аналіз витрат магазину, відображених на рахунках бухгалтерського обліку, на­ведено в табл. 2.3.

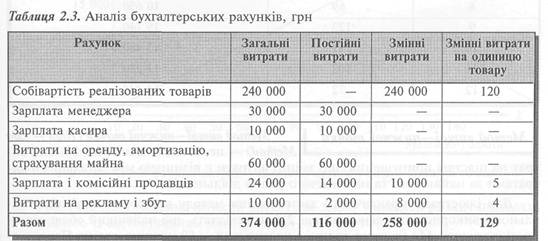
За результатами наведеного аналізу функцію витрат магазину "Час" можна описати так:

Y= 116 000+ 129х.

Отже, якщо в наступному періоді магазин планує збільшити обсяг продажу до 3 000 годинників*, а витрати на оренду будуть збільшені на 10 000, тоді загальні бюджетні витрати магазину становитимуть:

(116 000 + 10 000) + (129 ■ 3 000) = 126 000 + 387 000 = 513 000 грн.

Метод аналізу рахунків доволі широко використовують на практиці. Але слід зважати на те, що він значною мірою базується на досвіді та інтуїції менеджера й аналізі минулих подій. Через те його вадою є певна суб'єктивність і можливість суттєвих відмінностей між минулими та майбутніми умовами діяльності. Певною мірою уникнути зазначених вад можна за допомогою серії спостережень та засто­сування математичних методів.

Для розгляду решти методів скористаймося вихідними даними, наведеними у табл. 2.4. Це результати спостережень взаємозв'язку між часом роботи устатку­вання та витратами на його утримання за минулі дванадцять тижнів.

Метод вищої—нижчої точки І Метод вищої—нижчої точки (High — Low

ші^^^^т,^».^^»^»^^ Method) — це метод визначення функції ви-

трат на підставі припущення, що змінні витрати є різницею між загальними ви­тратами за найвищого та найнижчого рівнів діяльності.

Для ілюстрації практичного застосування методу вищої—нижчої точки ді­яльності використаємо дані таблиці 2.4, які свідчать, що найвищий обсяг діяль­ності становить 144 машино-годин, а найнижчий — 69 машино-годин. Перенесе­мо результати спостережень у табл. 2.5 і розрахуємо різницю між витратами у вищій та нижчій точках діяльності.

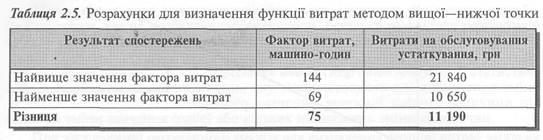
Отже, при зростанні обсягу діяльності на 75 машино-годин загальні витрати зросли на 11 190 грн. Звідси змінні витрати на 1 машино-годину становлять:

11 190: 75 = 149,2 грн.

Виходячи з цього, постійні витрати дорівнюють:

21 840 - (144-149,2) = 21 840 - 21 485 = 355 грн або:

10 650 - (69-149,2) = 10 650 - 10 295 = 355 грн.

Отже, функція витрат у цьому разі має такий вигляд:

7= 355 + 149,2х. Графічно цю функцію витрат зображено нарис. 2.19.

Графічне відображення функції витрат дає змогу уникнути ризику помилки, пов'язаного із застосуванням методу вищої—нижчої точки.

Річ у тому, що при використанні цього методу ми проводимо лінію функ­ції витрат через вищу і нижчу точку графіка, ігноруючи всі інші точки. Але якщо ці інші точки не мають тісного взаємозв'язку з вищою та нижчою точками (рис. 2.20), то функція витрат не відображатиме реальної залежності між ви­тратами та їхнім фактором.

Метод візуального пристосування

і Метод візуального пристосування (Visual-Fit \ Method) — графічний підхід до визначення функції \ витрат, за якого аналітик візуально проводить пряму лінію, беручи до уваги всі точки витрат.

Припустімо, що в нашому випадку аналітик, намагаючись врахувати всі точ­ки на графіку, провів лінію функції витрат таким чином (рис. 2.21):

З наведеного графіка видно, що постійні витрати становлять 5 000 грн. Для роз­рахунку змінних витрат використаємо дані при обсязі діяльності 132 машино-годин. У цій точці загальні витрати становлять 18 165 грн. Отже, змінні витрати дорівнюють:

18 165 - 5 000 = 13 165 грн. Відповідно, змінні витрати на 1 машино-годину становитимуть:

13 165: 132 = 99,7 грн. Функція витрат у цьому разі буде:

Y= 5 000 + 99,7х

Метод візуального пристосування дає змогу уникнути вад методу вищої— нижчої точки, але не гюзбавляє суб'єктивності, оскільки результати розрахунків суттєво залежать від точності ока й несхибності руки аналітика.

Регресійний аналіз

Регресійний аналіз (Regression Analysis) — статистич­на модель, яку використовують для визначення зміни середнього значення залежної змінної величини під впливом зміни значення однієї або кількох незалежних змінних величин.

При застосуванні регресійного аналізу для визначення функції витрат загальну суму витрат розглядають як змінну величину, залежну від певного чинника (обсягу виробництва, кількості замовлень тощо), який виступає як незалежна величина.

Лінійний взаємозв'язок між залежною та незалежною змінними величи­нами можна описати графічно як лінію регресії, або за допомогою формули (рівняння регресії).

Модель, яка використовує тільки одну незалежну змінну величину для ви­значення зміни незалежної змінної величини, називають простим регресійним аналізом. Вона має вигляд:

Y = а + Ьх

Модель, що використовує кілька незалежних змінних величин для визначен­ня зміни залежної змінної величини, має назву множинний регресійний аналіз і може бути описана так:

Y=a+b_lXl+b₂x₂+...+b_nx_n. (2.2)

На відміну від методу вищої-нижчої точки, регресійний аналіз враховує всі дані спостереження для визначення функції витрат.

Поряд із цим, регресійний аналіз уможливлює уникнення вад візуального підходу, оскільки передбачає застосування методу найменших квадратів.

Метод найменших квадратів (Least—Square Method) — це статистичний метод, який дає змогу розрахувати елементи функції витрат а і Ь так, що сума квадратів відстані від усіх точок сукупності, що вивчається, до лінії регресії є найменшою.

Сутність цього методу можна проілюструвати за допомогою графіка (рис. 2.22).

Для визначення функції витрат методом найменших квадратів необхідно роз­в'язати систему рівнянь:

Підставивши результати розрахунків у рівняння (2.3 і 2.4), одержимо:

187 515 = 12а + 1 2936 (2.5)

20 896 ПО = 1293а + 146 0256 (2.6)

Щоб розв'язати систему рівнянь для Ь, помножимо рівняння (2.5) на 107,75 (1 293: 12). Маємо:

20 204 741 = 1293а + 139 320,75 (2.7)

Тепер вирахуємо рівняння (2.7) з рівняння (2.6) і одержимо:

691 369 = 6704,256

Таким чином, b = 103.

Підставимо значення b у рівняння (2.5) і розв'яжемо його для а:

187 515 = 12а + (1 293 • 103)а = 4 528

Після заміни в рівнянні регресії коефіцієнтів а і b їхніми значеннями ми бачимо, що лінію регресії можна описати так:

7=4 528 + ЮЗх.

Спрощений статистичний аналіз

Цей метод запропонував український учений, академік М.Г. Чумаченко.

.шч^^ші-ш-ашш............ :_Ш.,.,....,..,..,,.1 Спрощений статистичний аналіз (Simplified

Statistical Analysis) — це метод визначення функції витрат, що передбачає розпо­діл показників на дві групи, виходячи зі зростання значення х, та розрахунок постійних витрат на основі середніх значень х і у.

Застосувавши цей підхід до прикладу, що розглядався раніше (табл. 2.4 і 2.6), одержимо:

Величину постійних витрат (а) визначають за формулою:

а = (УД - YJ_a) I (X_t - Х_о), (2.8)

де Y_Q і Y_l — середні значення витрат;

Х_о і Х_х — середні значення обсягу діяльності. Підставивши у наведену формулу розраховані середні значення Х\ Y, одержимо:

а = ((13 473 • 128) - (17 780 ■ 88)): (128 - 88) = 159 904: 40 = 3 998 грн.

Знаючи величину постійних витрат, можемо обчислити змінні витрати на одиницю (Ь):

b = (13 473 - 3 998): 88 = 107,7; або

Ь = (17 780 - 3 998): 128 = 107,7

Виходячи з цього, функція витрат, визначена за допомогою спрощеного ста­тистичного аналізу, є:

Y= 3 998 + 107, їх.

Вибір серед функцій витрат

Застосування різних методів для визна­чення функції витрат дає різні результати (див. табл. 2.7).

У розглянутому прикладі ми виходимо з припущення, що витрати змінюють­ся під впливом зміни часу роботи устаткування.

Але на практиці можуть бути й інші фактори витрат (кількість виготовленої продукції, вага матеріалів, кількість переналагоджень обладнання тощо).

Тому для прийняття управлінських рішень слід обрати найрелевантнішу функ­цію витрат. Для правильного вибору серед функцій витрат доцільно застосувати такі критерії:

• економічна правдоподібність;

• хороша пристосованість;

• значимість незалежних змінних величин.

Економічна правдоподібність означає, що взаємозв'язок між залежною змін­ною величиною (витратами) і незалежною змінною величиною (фактором ви­трат) має бути економічно доцільним.

Хороша пристосованість визначає, наскільки тісним є взаємозв'язок між ви­тратами та певним фактором, тобто наскільки точно функція витрат описує їхній взаємозв'язок.

Значимість незалежних змінних величин дає відповідь на питання: чи сут­тєво впливатиме на суму загальних витрат коливання значення (Ь) незалежної змінної величини?

Для визначення міри надійності функції витрат використовують коефіці­єнт детермінації, стандартну помилку обчислення і стандартну помилку кое­фіцієнта.

Надійність функції витрат ґрунтується на розмірі відхилень фактичного спо­стереження {Yd) від розрахункової величини на лінії регресії (Ye).

Коефіцієнт детермінації (Coefficient of Determination) характеризує питому ва­гу суми відхилень Y, що визначається незалежною змінною х у сумі загального відхилення і обчислюється за формулою:

Залишкова дисперсія (а_г²) визначає ту частину відхилень фактичних спостере­жень від лінії регресії, що зумовлена впливом випадкових або неконтрольованих чинників. Вона може бути встановлена як середнє значення квадрата різниці між фактичною та розрахованою величиною й обчислюється за формулою:

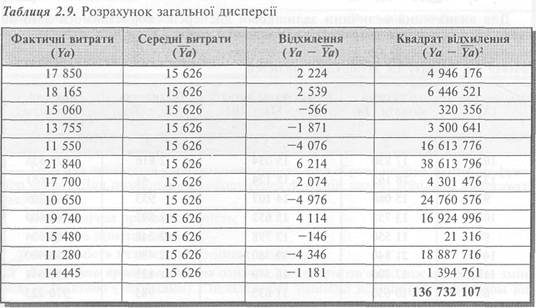
Для визначення величини залишкової дисперсії скористаймося даними табл. 2.6, а результати розрахунків викладемо в табл. 2.8.

Отже, о_г² = 65 435 532: 12 = 5 452 961.

Загальну дисперсію (о²) обчислюють як середнє значення квадрата різниці між Фактичною та сепедньоФактичною величиною Y:

У нашому прикладі середня сума фактичних витрат (Yd) становить:

15 626 (187 515: 12);

а розрахунок загальної дисперсії зробимо у таблиці 2.9.

Після розрахунку загальної та залишкової дисперсії ми можемо визначити коефіцієнт детермінації:

Я² = 1 - (65 435 532: 136 732 107) = 1 - 0,4786 = 0,5214.

Це означає, що 52,14% відхилень загальної суми витрат визначається зміна­ми величини зворотного фактора витрат, а решта 47,86% пояснюється впливом інших факторів та випадкових явищ.

Слід відзначити, що при значенні R² > 0,30 функція витрат вважається до­статньо надійною.

мал кла, має тис титі за с

рис (12 кол

сягз

Коефіцієнт детермінації свідчить про надійність оцінки загальних витрат, ґрунтованої на рівнинні регресії, але він не показує абсолютного розміру ймовір­ного відхилення від лінії регресії. Таку інформацію можна отримати, розрахував­ши стандартну помилку обчислення.

Стандартна помилка обчислення (Standard Error of Estimation) — це абсолют­ний розмір імовірного відхилення від лінії регресії.

Необхідність розрахувати стандартну помилку обчислення зумовлена тим, що лінію найменших квадратів ми розраховували на підставі вибіркових даних.

Тому цілком імовірно, що залежно від розміру вибірки ми одержимо різні оцінки функції витрат. Тільки розрахунок найменших квадратів на підставі спо­стереження всіх імовірних значень витрат на обслуговування устаткування дасть правдиву інформацію.

Тому виникає питання, наскільки наша лінія найменших квадратів (Y= 4 528 + + ЮЗх) наближена до справжньої лінії найменших квадратів.

Стандартна помилка обчислення дає змогу встановити інтервал, у межах якого ми можемо бути більш-менш переконані у правдивості наших оцінок. Цей інтер­вал залежить від бажаного рівня впевненості й має назву інтервал упевненості.

Інтервал упевненості (Confidence Range) — це діапазон, у межах якого існує упевненість щодо достовірності зроблених оцінок.

Стандартну помилку обчислення (S) визначають за формулою:

У наведеній формулі розмір вибірки (и) зменшений на 2, оскільки дві змінні величини (а і Ь) у рівнянні регресії були отримані шляхом дослідження цієї ви­бірки. Значення «— 2 називають ступенем свободи.

Розрахуємо стандартну помилку обчислення (S_e), скориставшись даними табл. 2.8. S_e =Л/ 65 435 532: 10 = 2 558,04

При обчисленні інтервалу упевненості слід зважати на величину вибірки.

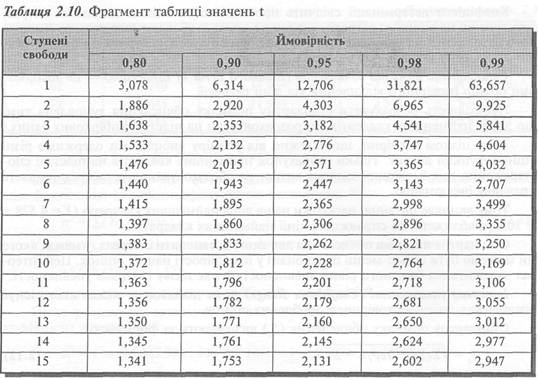
Теорія статистики свідчить, що розподіл точок навколо лінії регресії є нор­мальним у разі наявності щонайменше 30 спостережень. Оскільки в нашому при­кладі оцінка лінії регресії базується лише на дванадцяти спостереженнях, ми маємо скоригувати стандартну помилку обчислень за допомогою спеціальної ста­тистичної таблиці. Фрагмент такої таблиці наведено нижче (табл. 2.10); він міс­тить значення коефіцієнтів (t), необхідних для обчислення інтервалу впевненості за ступенів імовірності від 0,8 до 0,99.

Якщо ми хочемо визначити інтервал упевненості з імовірністю 99%, то ско­ристаємося останнім стовпчиком табл. 2.10 при значенні ступеня свободи =10 (12 — 2). Таким чином, ми можемо бути впевнені на 99%, що реальні витрати коливатимуться у межах ± 3,169 стандартної помилки.

Тобто, застосувавши отримані значення, наприклад для максимального об­сягу діяльності — 144 машино-години (табл. 2.4), одержимо:

19 360 ± 3,169 (2 558,04);

19 360 + 3,169 (2 558,04) = 27 466;

19 360 - 3,169 (2 558,04) = 11 254.

Отже, ми можемо бути впевнені на 99%, що за умови 144 машино-годин роботи устаткування витрати на його обслуговування коливатимуться у межах 11 254-27 466 грн.

Стандартна помилка коефіцієнта ( Standard Error of Coefficient) — це показ­ник, що відображає вплив випадкових чинників на величину коефіцієнта Ь (змінних витрат на одиницю).

Стандартну помилку коефіцієнта (S_b) обчислюють за формулою:

S_b = S_e:A/Z(x-*)² (2.13)

або

S_b = S_e:ЛІСЕ^ - хірс) (2.14)

Розрахуємо значення стандартної помилки коефіцієнта, виходячи з результа­тів попередніх розрахунків:

S_b = 2 558,04:Л/146 025 - (1 293²: 12) = 2 558,04 ^146 025 - 139 320,75 =

= 2 558,04 Л/б^704,25 = 2 558,04: 81,879 = 31,24

Співвідношення b/S_b > 2 означає, що ймовірність впливу випадкових факто­рів на коефіцієнт b у нашому прикладі незначна: 103: 31,24 = 3,30.

Отже, функція витрат, визначена шляхом регресійного аналізу, є достатньо надійною.

1. Як класифікують витрати підприємства?

2. Що таке вичерпані та невичерпані витрати?

3. Що таке витрати періоду та витрати на продукцію?Наведіть кілька прикладів цих витрат.

4. Що таке прямі та непрямі витрати? Наведіть приклади.

5. Що таке релевантні та нерелевантні витрати? Наведіть приклади.

6. Що таке середні та маржинальні витрати?Для чого їх обчислюють? Наведіть приклади.

7. Що таке альтернативні витрати? Наведіть приклад.

8. Що таке контрольовані та неконтрольовані витрати?

9. Що таке поведінка витрат?Які фактори на неї впливають? Наведіть приклади.

10. Наведіть приклади змінних витрат і відобразіть їхню поведінку графічно.

11. Наведіть приклади постійних витрат.

12. Що таке релевантний діапазон? Наведіть приклад.

13. Що таке напівзмінні витрати?Наведіть приклади й відобразіть графічно їхню поведінку.

14. У чому полягає вплив менеджера на величину витрат? Наведіть приклад дискрецій­них витрат.

15. Що таке функція витрат? Для чого її визначають?

16. Опишіть методи, які використовують для визначення функції витрат.

17. Що таке технологічний аналіз?

18. Що таке аналіз бухгалтерських рахунків?

19. Поясніть переваги та вади методу вищої—нижчої точки та методу візуального пристосування.

20. У чому полягають сутність і переваги регресійного аналізу?

21. Що таке спрощений статистичний аналіз?

22. Опишіть критерії оцінки функції витрат.

23. Які показники характеризують надійність функції витрат?Як їх визначити?

1. Апчерч А. Управленческий учет. — М.: Финансьі и статистика, 2002.

2. Вахрушина М.А. Бухгалтерский управленческий учет. — М.: Финстатинформ, 1999.

3. Друри К. Управленческий и производственньїй учет. — М.: ЮНИТИ-ДАНА, 2002.

4. Карпова Т.П. Основи управленческого учета. — М.: Инфра-М, 1997.

5. Управленческий учет / Под ред. А.Д. Шеремета. — М.: ФБК — ПРЕСС, 1999.

6. Хенсен Д.Р., Моувен М.М., Еліас Н.С., Сєнков Д.У. Управлінський облік. Пер. з англ. 5-го канад. вид. — К.: Міленіум, 2002.

7. Хорнгрен Ч., Фостер Г. Бухгалтерский учет: управленческий аспект. — М.: Финансьі и статистика, 1995.

8. Чумаченко Н.Г. Учет и анализ в промьішленном производстве СІЛА. — М.: Финансьі, 1971.

1.

Підприємство виробляє кріплення з алюмінію. Впродовж кварталу вироб­ничі витрати підприємства охоплювали:

Зарплату, грн Матеріали, грн

— верстатників 140 000 — алюміній 400 000

— майстрів 75 000 — запчастини для верстатів 36 000

— механіків 40 000. — мастильні матеріали 12 000.

Прямі витрати підприємства дорівнюють, грн:

а) 540 000; в) 651 000;

б) 592 000; г) 703 000.

Дата добавления: 2014-11-29