Дифференциальный метод

Методы определения ошибок механизмов

Всякий реальный механизм имеет погрешности (ошибки) звеньев и кинематических пар. Суммарные погрешности функционирования, приведенные к ведомому звену, являются результирующими. По величине ошибки положения или перемещения ведомого звена, ошибки мертвого хода оценивают точность механизма.

В теории точности механизмов рассматриваются и решаются две задачи. Первая или прямая задача заключается в определении суммарных ошибок положения и перемещения механизма или суммарной ошибки мертвого хода механизма по известным первичным ошибкам, лежащим в пределах допусков, зазоров. Вторая или обратная задача заключается в определении рациональных параметров, требований к точности изготовления и сборки деталей механизма по заданным величинам суммарных ошибок ведомого звена. Чаще рассматривают первую задачу. Существуют различные методы ее решения, в том числе аналитические, графоаналитические и графические. Рассмотрим некоторые из них.

Дифференциальный метод относится к аналитическим методам. Его сущность заключается в составлении уравнения, где положение ведомого рабочего звена механизма S выражено как функция некоторых параметров: координат ведущего звена x, y; размеров q₁; положения звеньев q₂ и т.п.

S = f (x, y, q₁, q₂, …, q_n). (4.7)

Уравнение можно составить, проектируя размеры звеньев кинематической схемы механизма на оси прямоугольной системы координат или используя соотношения размеров сторон и углов в геометрических фигурах, являющихся контуром механизмов.

Параметры x, y, q₁, q₂, …, q_n будем считать переменными, а их отклонения – первичными ошибками. Выражение полного дифференциала функции (4.7) будет равно .

Представим его как ошибку положения механизма

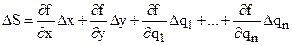. (4.8)

При Δx и Δy равных нулю выражение (4.8) примет вид

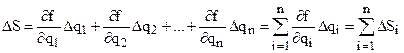, (4.9)

где Δq₁, Δq₂,…, Δq_n – первичные ошибки параметров q₁, q₂,…, q_n.

Ошибка положения механизма определяется как сумма нескольких слагаемых – частных ошибок ΔS_i, возникающих в результате действия отдельных первичных ошибок Δq_i. Величина частной ошибки ΔS_i зависит от величины первичной ошибки Δq_i и коэффициента ее влияния ∂f / ∂q_i. На основании принципа независимости действия ошибок i-ю частную ошибку ΔS_i можно найти, взяв производную от функции положении (4.7) по i-му параметру, считая все остальные параметры постоянными.

Метод позволяет найти ошибку положения механизма независимо от ее причины, если есть функциональная связь между положением рабочего звена и параметрами, содержащими ошибки. При данном методе не учитываются (что является недостатком) первичные ошибки параметров, не вошедших в уравнение (4.7) механизма.

Пример. Пусть звено 1 (рис. 4.11) кривошипно-ползунного механизма является ведущим, а звено 3 – ведомым. Найдем ошибку положения механизма, т.е. погрешность положения ΔS звена 3, определяемого координатой S. Погрешность возникает из-за ошибок в размерах звеньев: звена 1 – Δr; звена 2 – Δℓ и ошибки эксцентриситета Δh. Положение ведущего звена соответствует положению такого же звена идеального механизма, т.е. Δφ = 0.

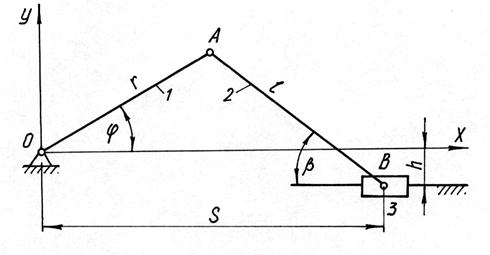
Рис. 4.11

Спроектируем план механизма на координатные оси x и y:

rcos φ + ℓcos β = S,

rsin φ + h = ℓsin β. (4.10)

Продифференцируем уравнения (4.10) по параметрам r, ℓ, h, S, β и, перейдя к первичным ошибкам параметров, получим

Δrcos φ + Δℓcos β – ℓΔβsin β = ΔS,

Δrsin φ + Δh = Δℓsin β + ℓΔβcos β. (4.11)

Погрешность угла Δβ является величиной неизвестной, возникающей из-за перечисленных выше первичных ошибок. Из второго уравнения (4.11) найдем Δβ:

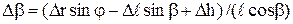
и, подставив его в первое уравнение (4.11), получим

ΔS = Δrcos φ + Δℓcos β – ℓ sin β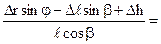

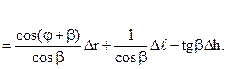(4.12)

Ошибку положения механизма можно представить как сумму частных погрешностей, возникающих от неточностей параметров r, ℓ, h, т.е.

как ΔS = ΔS_r + ΔS_ℓ + ΔS_h,

где 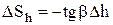. (4.13)

Дата добавления: 2014-11-29