Метод преобразованного механизма

Данный метод, относящийся к графоаналитическим, позволяет определить линейные зависимости ошибок положения механизма от первичных ошибок. Метод основан на идее построения схем преобразованных механизмов и планов малых перемещений. Из выражения (4.9) имеем

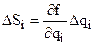, (4.14)

где ∂f/∂q_i – функция, показывающая влияние соответствующей первичной ошибки Δq_i на суммарную ошибку ΔS механизма. Но эту функцию

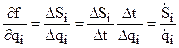(4.15)

можно рассматривать как отношение перемещений или отношение скоростей (передаточное отношение) ведомого и ведущего звеньев преобразованного механизма.

Преобразование механизма заключается в том, что ведущее звено действительного механизма закрепляют в заданном положении, а звено, содержащее погрешность, превращается в ведущее с направлением движения, совпадающим с направлением изменения параметра исследуемого звена. Если ведущему звену преобразованного механизма сообщить скорость, пропорциональную первичной ошибке, то ведомое звено получит скорость, пропорциональную частной ошибке механизма. Поэтому планы малых перемещений преобразованных механизмов строятся так же, как и планы скоростей.

Из плана малых перемещений (плана скоростей) преобразованного механизма определяют частную ошибку положения механизма из-за соответствующей первичной ошибки и передаточного отношения между ними.

Рассматриваемый метод позволяет находить частные погрешности ΔS_i механизма, не прибегая к составлению его функции положения, которая часто бывает очень сложной. Данный метод применим для механизмов с низшими и высшими кинематическими парами (кулачковые механизмы), его используют для оценки влияния на погрешность механизма ошибок размеров звеньев, величин зазоров в кинематических парах.

Пример. Рассмотрим приложение этого метода на примере внецентрального кривошипно-ползунного механизма (рис. 4.11). Ошибка механизма может произойти из-за первичных ошибок в размерах кривошипа r, шатуна ℓ и эксцентриситета h. Для учета влияния ошибки размера Δr кривошипа 1 строим преобразованный механизм (рис. 4.12, а). Закрепим ведущее звено 1, по нему в направлении первичной ошибки Δr будем перемещать дополнительное звено 1′. Из точки (полюса) р в направлении ошибки Δr откладываем в масштабе μ отрезок ра = Δr /μ, приняв его за скорость точки А звена 1′. Скорость (перемещение) точки В звена 3 можно выразить, рассматривая соответственно движение звена АВ () и ползуна относительно направляющих (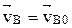). Решая графически приведенные уравнения, из точки а проводим отрезок a b, параллельный вектору 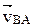, т.е. перпендикулярный звену АВ, а из полюса р – прямую, параллельную направляющим ползуна. Отрезок рb в масштабе равен частной ошибке ΔS_r = |pb|·μ. Так как угол pb a = 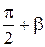, а угол p a b = , отношение . 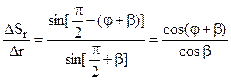Откуда

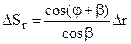. (4.16)

Аналитическим путем из планов малых перемещений (рис. 4.12, б, в) получим значение ΔS_ℓ и ΔS_h. Частную погрешность ΔS_i считаем положительной, если направление вектора 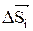совпадает с направлением отсчета положений S ведомого звена. Полученные из планов малых перемещений зависимости ΔS_r, ΔS_ℓ, ΔS_h соответствуют выражениям (4.13).

При допущении, согласно которому ошибки размеров звеньев настолько малы, что направления звеньев реального и теоретического механизмов совпадают, можно строить единый план малых перемещений для определения ошибки механизма с учетом первичных ошибок всех его звеньев.

Сделаем размеры r, ℓ, h механизма (рис. 4.13, а) переменными и построим преобразованный механизм с тремя степенями свободы движения (рис. 4.13, б).

Строим картину малых перемещений преобразованного механизма, сообщая каждому звену малое перемещение, равное Δq_i. Из точки (полюса) р (рис. 4.13, в) проводим вектор , перпендикулярный к направляющей ползуна 3 в направлении ошибки Δh эксцентриситета h и равный ей по величине (|pb| = Δh/ μ); из полюса р проводим вектор в направлении ошибки Δr, т. е. параллельный кривошипу 1 и равный по величине погрешности Δr длины кривошипа (|p а | = Δr/ μ); из точки а проводим вектор 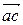в направлении ошибки Δℓ, т. е. параллельный шатуну 2 и равный ошибке Δℓ длины шатуна ℓ (| а с| = Δℓ/ μ).

Далее через точку с проводим линию, перпендикулярную шатуну 2, а через точку b – линию, параллельную направляющей ползуна. Замыкающая 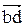представляет ошибку ΔS механизма, т.е. ΔS = |bd| ·μ.

в

б

а

Рис. 4.12

Дата добавления: 2014-11-29