Пример 7. Определить реакцию составной рамы, возникающую от действия сил и

Определить реакцию составной рамы, возникающую от действия сил и . Реакцию будем находить через составляющие 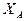и (рис. 2.18).

Рис. 2.18

Определение 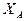(рис. 2.19)

Рис. 2.19

Для вычисления 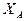заменим неподвижную опору шарнирной подвижной, способной перемещаться в горизонтальном направлении, и искомой силой X_A.

Полученный при этом механизм имеет одну степень свободы. Теперь точка 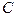может получить возможное перемещение перпендикулярно
к (опора остаётся неподвижной, точка 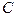принадлежит правой части рамы).

Учитывая, что шарнир 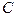одновременно принадлежит и левой части рамы, и что точка может получить горизонтальное смещение, находим мгновенный центр поворота левой части рамы – точку 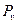. Активные силы, приложенные к левой части, включая и неизвестную 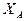, совершают работу на повороте 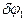полурамы вокруг 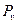, а силы, приложенные к правой части рамы, – соответственно на повороте 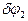вокруг опоры .

Записываем уравнение работ в виде:

.

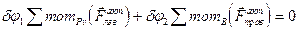Вычисляя моменты сил и связывая между собой повороты 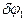и 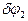соотношением 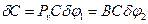, получаем

.

Откуда

.

Определение (рис. 2.20)

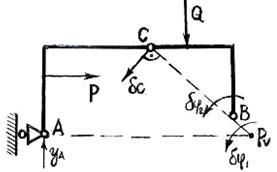
Рис. 2.20

Для вычисления вертикальной составляющей реакции заменяем неподвижную опору подвижной, способной перемещаться вертикально. И даём системе возможное перемещение, при котором правая часть поворачивается вокруг неподвижной точки В. За счет этого точка С перемещается перпендикулярно ВС. Так как точка А может перемещаться только вертикально, найдем мгновенный центр поворота левой части – точку .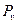

Составляем уравнение работ и находим зависимость между углами поворотов левой и правой части:

.

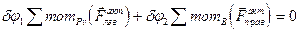Из условия получаем

,

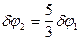откуда .

Применённый метод избавил нас от необходимости решения системы шести уравнений с неизвестными , которую мы получили бы при решении задачи методами статики.

Дата добавления: 2014-11-29