К исследованию равновесия механизмов

Применение принципа возможных перемещений

Принцип возможных перемещений очень эффективен при исследовании равновесия плоских механизмов, т.е. таких, звенья которых движутся в плоскостях, параллельных какой-то неподвижной плоскости. Упрощённо можно считать, что все точки и звенья его движутся по плоскости самого рисунка.

Считая, что все соединения звеньев механизма, как и внешние связи, являются идеальными, мы исключаем из рассмотрения их реакции. Это и определяет преимущества принципа возможных перемещений по сравнению с методами геометрической статики (уравнения равновесия).

Пример 5

Пренебрегая трением, найти соотношение между силами P и Q, при котором кривошипно-ползунный механизм будет находиться в равновесии, если сила перпендикулярна OA (рис. 2.8).

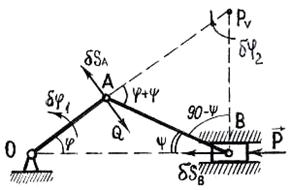
Рис. 2.8

Сообщив механизму возможное перемещение, и приравнивая к нулю сумму работ сил P и Q на этом перемещении, получим

P × dS_В – Q×dS_А = 0,

откуда

,

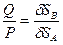где dS_A и dS_B – модули возможных перемещений точек А и В.

Перемещение dS_A перпендикулярно OA, dS_B направлено по прямой OB. Для определения зависимости между dS_B и dS_A найдём МЦС звена АВ. Он лежит на пересечении перпендикуляров и к направлениям возможных перемещений точек А и В. Эти перемещения находятся в такой же зависимости, как скорости точек А и В, т.е.

,

поэтому

.

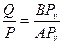Введя обозначения углов j и y, из по теореме синусов находим

,

откуда

.

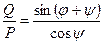Зависимость между возможными перемещениями dS_A и dS_B можно определить, используя теорему о проекциях скоростей точек A и B на прямую АВ. По этой теореме можно записать:

dS_A cos [90 – (j + y)] = dS_B × cosy,

откуда

.

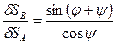Рассмотренную задачу можно было бы решать, применяя методы статики твёрдого тела. Для этого нужно составить уравнения равновесия для каждого звена механизма (кривошипа ОА, шатуна АВ, ползуна В); при этом пришлось бы принять во внимание неизвестные реакции связей (реакции в шарнирах А и В и реакцию направляющих, в которых движется ползун).

При решении задач подобного рода преимущество принципа возможных перемещений очевидно; этот метод позволяет исключить из рассмотрения неизвестные реакции связей, т.к. эти реакции в условие равновесия системы, выраженное принципом возможных перемещений, не входят.

2.6. Применение принципа возможных перемещений

к определению реакций связей

В формулировке принципа возможных перемещений силы реакции не фигурируют. Тем не менее, принцип возможных перемещений можно эффективно применять для определения этих сил, и чем сложней конструкция, тем больше преимущества принципа возможных перемещений по сравнению с методами, применяемыми в геометрической статике (составление и решение уравнений равновесия).

Статические сооружения (конструкции) имеют нулевую степень подвижности, т.е. находятся в равновесии благодаря наличию внешних и внутренних связей. Связь в виде жесткой заделки, наложенная на тело, ограничивает любые его перемещения, поэтому реакцию представляем в виде двух составляющих, направленных по осям координат, и реактивного момента. Шарнирно-неподвижная опора ограничивает перемещение тела по двум взаимно перпендикулярным направлениям, ее реакцию представляем в виде двух составляющих по осям координат.

Применяя принцип освобождаемости от связей, можно отбросить отдельно взятую связь, ограничивающую перемещение тела в одном направлении, заменив ее силой реакции.

В тех случаях, когда связь препятствует перемещению тела в нескольких направлениях (неподвижная шарнирная опора, жесткая заделка), она заменяется другим типом связи, допускающим перемещение в направлении той реакции, которую хотим определить.

Для определения реактивного момента в жесткой заделке она заменяется неподвижной шарнирной опорой и искомым реактивным моментом (рис. 2.9).

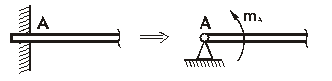
Рис. 2.9

Для определения горизонтальной или вертикальной составляющей реакции жесткой заделки она заменяется связью типа стержень в направляющих и искомой реакцией (рис. 2.10, 2.11).

Рис. 2.10

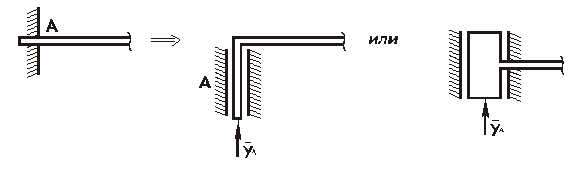
Рис. 2.11

Таким способом можно последовательно определить реакции всех связей. При этом каждый раз отбрасывается та связь, реакцию которой требуется определить, и механическая система получает одну степень свободы.

В тех случаях, когда связь препятствует перемещению тела в нескольких направлениях (неподвижная шарнирная опора, жёсткая заделка), она отбрасывается не полностью, а лишь заменяется более простой. Как это делается, показано на рис. 2.12.

Покажем варианты замены шарнирно-неподвижной опоры при определении её реакций.

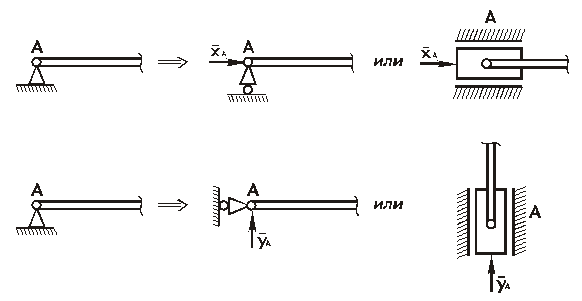
Рис. 2.12

Рассмотрим примеры определения опорных реакций составных
конструкций.

Дата добавления: 2014-11-29