Пример 8

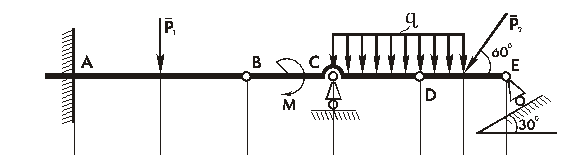
Конструкция, состоящая из 3-х балок, соединенных шарнирами B и D, находится в равновесии под действием произвольной плоской системы сил (рис. 2.21). На неё наложены внешние связи: в точке А – жесткая заделка;
в точках С и Е – подвижные шарнирные опоры.

Определить реакции внешних связей.

Исходные данные: P ₁ = 12 кH; P ₂ = 20 кH; M = 50 кH×м; q = 2 кH/м.

4 4 4 4 2 2

Рис. 2.21

Решение:

Упростим расчетную схему нагружения. Распределенная нагрузка действует на две балки ВD и DE, являющиеся абсолютно твердыми телами, поэтому заменим её равнодействующими Q ₁ и Q ₂, приложенными в середине участков распределения и равными:

Q ₁ = q · l _CD = 2·4 = 8 кH;

Q ₂ = q · l _DК = 2·2 = 4 кH.

Определение R _E (рис. 2.22).

Рис. 2.22

Подвижная шарнирная опора Е препятствует перемещению точки Е в направлении перпендикулярной опорной поверхности, поэтому для определения её реакции отбросим опору и заменим её действие искомой силой – R _E. Составная балка преобразовалась в изменяемую систему. Дадим системе возможное перемещение. Балка АВ, один конец которой жестко защемлён, останется неподвижной; часть балки ВD могла бы повернуться вокруг неподвижной точки В, но наложенная связь в виде шарнирно-подвижной опоры в точке С, лишает балку ВD подвижности. Возможное перемещение балки DЕ будет представлять собой поворот вокруг точки D на угол δφ.

На этом возможном перемещении составной конструкции совершают работу только силы Q ₂; P ₂; R _E.

Составим уравнение возможных работ:

.

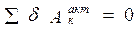Так как балка DE совершает поворот вокруг точки D, то суммарную элементарную работу этих сил можно вычислить как

.

(– Q ₂· DL – P ₂· sin 60º· DK + RE · cos 30º· DE)· δφ = 0.

Так как δφ ¹ 0, то после сокращения на δφ, получим уравнение, из которого находим R _E:

R _E = 11,2 кH.

Определение R _C (рис. 2.23).

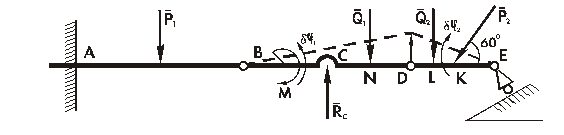
Рис. 2.23

В точке С на балку наложена связь в виде шарнирно-подвижной опоры, направление её реакции известно. Отбрасываем эту опору и заменяем её реакцией R _C, которую теперь можно считать активной силой. Система стала мгновенно изменяемой, и ей можно сообщить возможное перемещение, при котором балка АВ останется неподвижной; балка ВD повернётся на угол δφ ₁ относительно неподвижной точки В, а балка DE повернётся на угол δφ ₂ относительно своего МЦС, совпадающего с точкой Е.

Составим уравнение работ, выражающее принцип возможных перемещений в этом случае

.

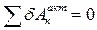(– M + R _C· CB – Q ₁· BN)· δφ ₁ + (– Q ₂· LE – P ₂· sin 60º· KE)· δφ ₂ = 0.

Для решения полученного уравнения находим зависимость между δφ ₁ и δφ ₂ через перемещение точки D.

δS _D = BD · δφ ₁ = ED · δφ ₂,

отсюда .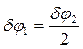

С учетом этого находим R _C = 47,8 кH.

Определение Y _A (рис. 2.24).

Для определения Y _A – вертикальной реакции жесткой заделки – видоизменим её таким образом, чтобы точка А могла перемещаться только вертикально, но при этом исключалась возможность перемещения, при котором балка АВ сместится поступательно на δS _А, например, вертикально вверх. Такое же перемещение получит точка В: δS _В = δS _А.

Рис. 2.24

Балка BD повернется на угол 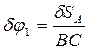вокруг точки С (МЦС балки ВD). Тело DE повернется относительно точки Е на угол δφ ₂.

Составляем уравнение работ:

.

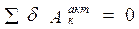Y _A· δS _А – P ₁· δS _А + (M + Q ₁· NC)· δφ ₁ + (Q ₂· LE + P ₂· sin 60º· KE) δφ ₂ = 0.

Находим зависимость между возможными перемещениями балок АВ, ВD и DЕ:

δS _В = δS _А; δS _В = ВС · δφ ₁; δS _D = CD · δφ ₁; δS _D = DЕ · δφ ₂.

Так как ВС = 4 м; DC = 4 м; DE = 4 м, то .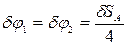

С учетом этих зависимостей определяем Y _А = –16,2 кH.

Определяем Х _А (рис. 2.25).

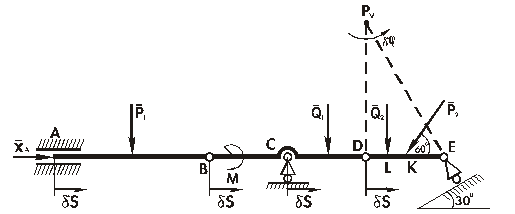
Рис. 2.25

В этом случае видоизменяем жесткую заделку так, как это показано на рис. 2.12. Полученной системе сообщаем возможное перемещение, при котором балки АВ и BD будут смещаться поступательно на δS, например, вправо, а балка DЕ повернется относительно МЦС (точка P _V) на угол δφ.

Составляем уравнение работ:

.

Х _A· δS + (– Q ₂· DL – P ₂· cos 60º· DP _V – P ₂· sin 60º· DK)· δφ = 0.

Зависимость между возможными перемещениями:

δS = DP _V· δφ.

Учитывая это, находим Х _А=15,6 кH.

Определение m _A (рис. 2.26).

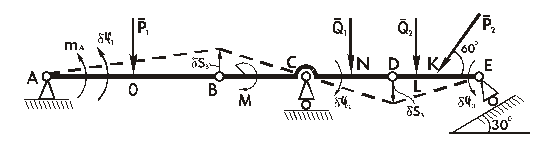
Рис. 2.26

Для определения реактивного момента в жесткой заделке заменяем её шарнирно-неподвижной опорой, ограничивающей любые перемещения балки, кроме её вращения относительно шарнира А. Дадим балке АВ возможное перемещение, в результате которого она повернётся на угол δφ ₁, против хода часовой стрелки, балки BD и DE повернутся при этом относительно точек С и Е (эти точки являются мгновенными центрами скоростей балок ВС и DE) на углы δφ ₂ и δφ ₃ соответственно.

Составляем уравнение работ

.

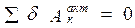(m _A – P ₁· AО)· δφ ₁ + (M + Q ₁· CN)· δφ ₂ + (Q ₂· LE + P ₂· sin 60º· KE)· δφ ₃ = 0.

Находим зависимость между δφ ₁, δφ ₂ и δφ ₃.

По рис. 2.26 имеем:

δS _В = АВ · δφ ₁ = CВ · δφ ₂,

δS _D = CD · δφ ₂ = ЕD · δφ ₃.

Так как АВ = 8 м; ВС = 4 м; CD = 4 м; ЕD = 4 м, получаем:

δφ ₂ = 2· δφ ₁, δφ ₂ = δφ ₃.

Выполним проверку правильности решения задачи, для чего составим известное из статики уравнение равновесия для всей конструкции в целом (рис. 2.27).

Рис. 2.27

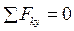: Y _A – P ₁ + R _C – Q ₁ – Q ₂ – P ₂· sin 60º + R _E· cos 30º = 0,

–16,2 – 12 + 47,8 – 8 – 4 – 20·0,866 + 11,2·0,866 = 0,

0 = 0.

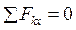: Х _А – R _E· sin 30º = 0,

15,6 – 11,2·0,5 = 0,

0 = 0.

:

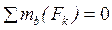Y _A· AО + P ₁· OB – M + m _A + R _C· BC – Q ₁· BN – Q ₂· BL –P ₂· sin 60º· OK +
+ R _E· cos 30º· BE = 0,

после подстановки всех заданных величин получаем 0 = 0.

Реакции опорных устройств найдены верно.

Пример 9

Рис. 2.28

Плоская рама, состоящая из 3-х тел, соединённых шарнирами В и С, находится в равновесии под действием произвольной плоской системы сил (рис. 2.28). Определить реакции внешних опорных устройств, применяя принцип возможных перемещений. Выполнить проверку правильности решения. Исходные данные: F 1 = 25 кН; F 2 = 20 кН; M = 40 кН×м; q = 1,0; sin a = 0,6. Линейные размеры принять непосредственно из рисунка, выполненного в указанном масштабе.

Решение

Заменяем распределённую нагрузку равнодействующей, равной
Q = q ×4 = 10×4 = 40 кН, приложенной в середине участка.

Определение U _Д (рис. 2.29).

Рис. 2.29

Заменим шарнирно-подвижную опору Д вертикально-подвижной шарнирной опорой и приложим к ней искомую силу U Д. Изменённой таким способом системе сообщаем возможное перемещение, при котором точка Д перейдёт, например, в положение Д¢. Так как шарнир Б остаётся неподвижным, то стержень ВС повернётся на некоторый угол dj вокруг этой точки. При этом точка С получит возможное перемещение dS c, перпендикулярное ВС. В итоге тело СД сместится поступательно вверх на dSc = dSд.

Составляем уравнение работ:

.

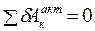U _Д – dS _д – Q ×2 dj = 0.

Находим зависимость между dS _с и dS.

Из прямоугольного треугольника ВСС¢ имеем:

dS _с = ВС × dS = 4 dj.

Подставляя эту зависимость в уравнение работ и сокращая на dj, находим U _Д = 20 кН.

Определение Х _Д (рис. 2.30).

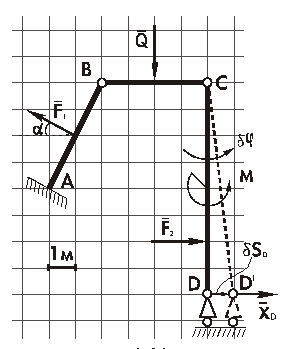Рис. 2.30

Заменим шарнирно-подвижную опору Д шарнирной горизонтально-подвижной опорой и реакцией Х Д. Дадим системе возможное перемещение, при котором точка Д сместится горизонтально вправо на расстояние dS д. Стержень ДС повернётся вокруг точки С (мгновенного центра скоростей тела ДС) на угол dj. Составляем уравнение работ: 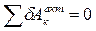. (М + F 2×6)dj + ХD×dSд = 0.

Определяем зависимость между возможными перемещениями:

dS _д = ДС × dj = 8 dj.

Подставляя в уравнение работ, и сокращая на dj ¹ 0, находим
Х _Д = –20 кН.

Определение Y _A (рис. 2.31).

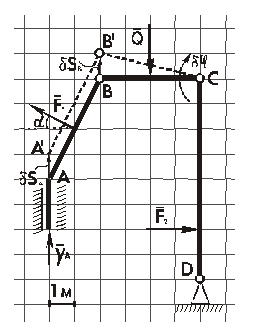Рис. 2.31

Заменим жесткую заделку в точке А такой связью, которая позволяет этой точке перемещаться в вертикальном направлении, т.е. в направлении искомой составляющей реакции жесткой заделки. Одновременно новая связь, наложенная на систему в точке А, должна препятствовать любым другим перемещениям тела АВ, в частности – повороту вокруг точки А. В результате стержень АВ переместится поступательно, на величину dS A = dS B, а стержень ВС повернется на угол dj вокруг точки С (МЦС тела DC).

Составляем уравнение работ:

.

.

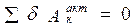Находим зависимость между перемещениями:

.

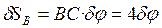Подставляя в уравнение эту зависимость, и сокращая на dj ¹ 0, находим Y _A = 5 кН.

Определение Х _А (рис. 2.32).

Заменим жёсткую заделку в точке А новым типом связи и искомой составляющей реакции жёсткой заделки. Сообщаем системе возможное перемещение, в результате которого точки А и В получат перемещения
dS _А = dS _В. Стержень ДС повернётся на угол dj вокруг токи Д, а точка С получит перемещение dS _c, перпендикулярное ДС, т.е. тоже горизонтальное. Поэтому стержень ВС переместится поступательно, и dS _С = dS _В. Точки А и В перейдут в положения А ¢ и В ¢ при поступательном горизонтальном перемещении тела АВ, т.е. dS _С = dS _В, АА ¢ = ВВ ¢

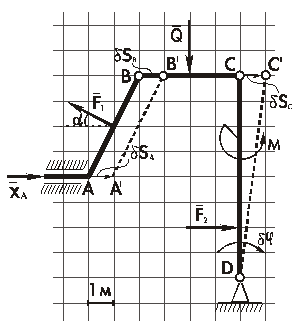Рис. 2.32

Составляем уравнение работ 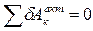. (X A – F 1 cosa) dS A + (– M + F 2×2) dj = 0. Зависимость между возможными перемещениями точек А, В, С и тела ДС: dS А= dS В = dS С = 8 dj. Учитывая это соотношение, из уравнения работ находим Х А= 20 кН.

Определение m _A (рис. 2.33).

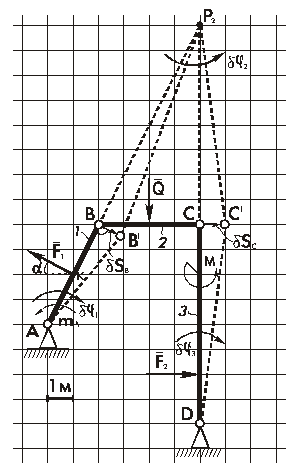Рис. 2.33

Для определения реактивного момента в жесткой заделке заменим её шарнирно-неподвижной опорой и искомым моментом m A. Сообщим системе возможное перемещение, при котором стержень АВ повернется на угол dj 1 вокруг неподвижной точке А, а стержень DC повернется вокруг тоже неподвижной точки D на угол dj 3, а стержень ВС повернется на угол dj 2 вокруг своего МЦС – точки Р 2. Составим уравнение работ: :

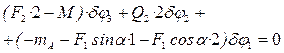
Находим зависимость между перемещениями:

δS _В = АB · δφ ₁ = ВР ₂· δφ ₂

δS _С = Р ₂ С · δφ ₂ = DС · δφ ₃.

Определив линейные размеры АВ, ВР ₂, Р ₂ С и DС непосредственно по рисунку, получаем:

;

4 δφ ₃ = 4 δφ ₂.

Отсюда δφ ₁ = 2· δφ ₂; δφ ₃ = δφ ₂.

Подставляя в уравнения работ эти зависимости и сокращая на dj₂ ¹ 0, находим m _а = –15 кН×м.

Выполним проверку правильности полученных результатов (рис. 2.34).

Рис. 2.34

Для чего составим уравнение равновесия всей конструкции в целом виде: 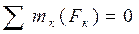, Х А×2 – U А×1 + m А – Q ×3 + M + F 2×4 + Х D×6 + U Д×5 = 0, 0 = 0. Реакции внешних связей конструкции определены верно.

Дата добавления: 2014-11-29