Линия на координатной плоскости

ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

КНИГА 3

Отпечатано в типографии

Электрические аппараты

Редактор Г.В. Загребина

Технический редактор В.Ф. Елисеева

Оригинал-макет Е.Э. Парсаданян

Подп. в печать 00.00.09

Формат 60х841/16. Бумага офсетная.

Печать офсетная. Усл. п. л. 3.

Усл кр. отт. 4,83. Уч.-изд. л. 3.

Тираж 75 экз. С.-

___________________________________________________________________

Государственное образовательное учреждение

высшего профессионального образования

«Самарский государственный технический университет»

443100 г. Самара, ул. Молодогвардейская, 244. Главный корпус

Самарского государственного технического университета

443100 г. Самара, ул. Молодогвардейская, 244. Корпус N 8

Аналитическая геометрия – это раздел математики, в котором геометрическим объектам ставят в соответствие определенные уравнения таким образом, что свойства объектов выражаются в свойствах этих уравнений. Уравнения записывают относительно избранной системы координат. Если геометрический объект рассматривать как некое точечное множество, то уравнение геометрического объекта – это правило отбора точек пространства во множество, образующее данный геометрический объект.

ГЛАВА 1

Предположим, что на координатной плоскости хОу задана некоторая линия. Тогда точки плоскости можно разделить на две категории, одни из которых принадлежат данной кривой, а другие ей не принадлежат.

Определение 1. Уравнение 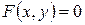, которому удовлетворяют координаты х, у всех точек линии и не удовлетворяют координаты точек, не принадлежащих этой линии, называется уравнением линии на плоскости в декартовой системе координат.

В частности, уравнение линии может представляться в виде явной функции .

Примеры.

1. Окружность радиуса R с центром в точке М (х ₀, у ₀). Ее уравнение

.

2. Цепная линия. Ее уравнение

.

По такой линии устанавливается в равновесии гибкая и нерастяжимая тяжелая нить (цепь, провод и т.п.), подвешенная за оба конца.

Определение 2. Параметрическими уравнениями линии в декартовой системе координат на плоскости называются уравнения вида

, ,

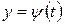где функции и 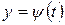имеют одну и ту же область определения. Каждому значению t из этой области соответствует точка М () рассматриваемой линии и каждая точка М этой линии соответствует некоторому значению t из области определения функций и 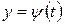, т.е. для любой точки М линии найдется такое значение t, что 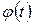и будут координатами точки М.

Например, параметрические уравнения окружности радиуса R с центром в точке М (х ₀, у ₀) имеют вид

, .

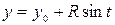Дата добавления: 2014-11-29