Временные ряды

Реализация задания на компьютере с помощью ППП Ехсеl

Исходным статистическим материалом для решения задач этой темы являются задания из раздела «Множественная регрессия». Каждому студенту необходимо уравнение множественной регрессии, полученное в Главе II, проверить на предмет нарушения предпосылок МНК и при необходимости произвести коррекцию модели.

4.2.1. Проверка наличия гетероскедастичности

Задание:

1) Графически и с помощью тестов проверить наличие гетероскедастичности;

2) При наличии гетероскедастичности с помощью тестов Уайта, Парка и Глейзера выбрать наилучшую аппроксимацию или 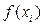(по значению коэффициента детерминации R ²) и с помощью ВМНК скорректировать уравнение регрессии.

Пример 4.1. В табл. 4.1 приведены данные об объеме импорта Y (млрд долл.), валовом национальном продукте Х ₁ (млрд долл.) и индексе потребительских цен Х ₂ в США за период с 1964 по 1979 гг.

Таблица 4.1

Годы	Y	Х 1	Х 2
	28,4	635,7	92,9
	32,0	688,1	94,5
	37,7	753,0	97,2
	40,6	796,3	100,0
	47,7	868,5	104,2
	52,9	935,5	109,8
	58,5	982,4	116,3
	64,0	1063,4	121,3
	75,9	1171,1	125,3
	94,4	1306,6	133,1
	131,9	1412,9	147,7
	126,9	1528,8	161,2
	155,4	1702,2	170,5
	185,8	1899,5	181,5
	217,5	2127,6	195,4
	260,9	2368,5	217,4

Параметры множественной регрессии определим с помощью функции ЛИНЕЙН и построим графики и (рис. 4.1.).

Из рисунка видно, что уравнение множественной регрессии имеет вид:

.

Качество уравнение регрессии в целом достаточно высокое (R ² = 0.987). Из графиков распределения видно, что ошибки зависят от факторов, причем эта зависимость имеет явно нелинейный характер. Однозначно из графиков сказать нельзя присутствует ли гетероскедастичность и в какой степени. Если гетероскедастичность существует, то носит явно нелинейный характер. Поэтому проверки с помощью тестов Спирмена и Голдфелда-Квандта здесь не правомочны. Покажем это.

Тест ранговой корреляции Спирмена.

Результаты реализации этого теста на компьютере представлены на рис.4.2.

Рис. 4.1

Х1	модЕ	Ранг Х	Ранг Е	dкв		Коэф. Ранговой корр. Спирмена	0,123529
635,7	9,494539
688,1	7,765652					Т набл =	0,465772
	6,320676
796,3	3,696187					Ткрит =	2,160369	(для аl =0,05)
868,5	1,940079
935,5	2,369626
982,4	5,383489
1063,4	10,03754
1171,1	9,629909
1306,6	7,688036
1412,9	10,38887
1528,8	13,95374
1702,2	6,12615
1899,5	0,434927
2127,6	3,677338
2368,5	11,47022

Рис. 4.2

Обозначения на рисунке имеют следующий смысл:

модЕ = ; dкв = (ранг х _i - ранг )².

Для вычисления рангов была использована статистическая функция РАНГ(число; массив; порядок), которая возвращает ранг числа из массива. Если порядок = 1, то ранжирование по возрастанию, если порядок =0 - ранжирование по убыванию.

Так как Т _набл , то коэффициент ранговой корреляции Спирмена статистически не значим, что является признаком отсутствия гетероскедастичности в смысле Спирмена (что априорно и предполагалось).

Тест Голдфелда-Квандта.

В связи с тем, что выборка небольшая (n = 16), принимаем k = 8. Результаты анализа с помощью этого теста представлены на рис. 4.3.

Х1	Y		Линейн			Х1	Y		Линейн
635,7	28,4		0,085431	-26,5681		1171,1	75,9		0,148877	-95,4629
688,1			0,001743	1,484911		1306,6	94,4		0,007266	12,5994
	37,7		0,997508	0,685035		1412,9	131,9		0,985909	8,008884
796,3	40,6		2401,455			1528,8	126,9		419,816
868,5	47,7		1126,939	2,815641		1702,2	155,4		26927,94	384,8534
935,5	52,9					1899,5	185,8
982,4	58,5					2127,6	217,5
1063,4						2368,5	260,9

Рис. 4.3

Из рисунка видно, что S₁ = 2,816, а S₂ = 384,85, в результате чего

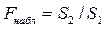= 136,68 > f_кр = 4,28, что с одной стороны свидетельствует о значительных расхождениях отклонений в начале и в конце списка данных, но это обусловлено двумя «выбросами» (см. рис. 4.1), а вовсе не тенденцией .

Как уже было отмечено выше, наиболее подходящим тестом для выявления гетероскедастичности, в этом случае, является тест Уайта.

Тест Уайта.

В этом тесте будем предполагать, что квадраты ошибок можно представить уравнением вида:

Результаты расчетов с помощью функции Линейн представлены на рис.4.4. Из рисунка следует (2,442274) < (3,325835), что свидетельствует об отсутствии регулярности ошибок, а это значит гетероскедастичностью можно пренебречь.

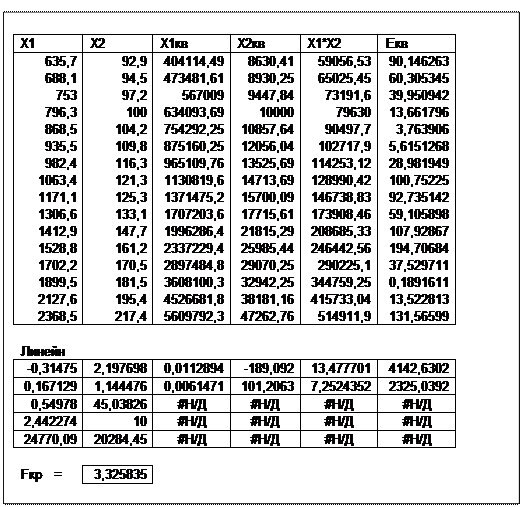
Рис. 4.4

Если бы факт гетероскедастичности подтвердился, то все составляющие исходного уравнения

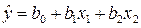
необходимо разделить на 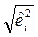, которые для данного примера вычисляются по формуле:

,

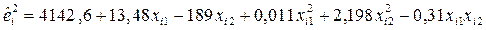и оценить его. В результате чего уравнение регрессии будет адаптировано к переменным дисперсиям ошибок измерений.

4.2.2. Проверка наличия мультиколлинеарности

Решение данной задачи рассмотрим на Примере 4.1.

Результаты вычислений с помощью ППП Ехсеl представлены на рис.4.5. Парные коэффициенты корреляции (Х ₁, Х ₂) и (Y, Х ₁, Х ₂) были получены с помощью функции Корреляция. Доступ к этой функции осуществляется следующим образом:

1) в главном меню выберите Сервис/Анализ данных/Корреляция (рис.4.6). Щелкните по кнопке ОК;

				Корреляция 1
Y	Х1	Х2			Х1	Х2
28,4	635,7	92,9		Х1		0,9971653
	688,1	94,5		Х2	0,9971653
37,7		97,2
40,6	796,3			det R	Хи кв.	Хи кв.кр.
47,7	868,5	104,2		0,0056613	13,874514	5,0238865
52,9	935,5	109,8
58,5	982,4	116,3		Корреляция 2
	1063,4	121,3			Y	Х1	Х2
75,9	1171,1	125,3		Y
94,4	1306,6	133,1		Х1	0,9931772
131,9	1412,9	147,7		Х2	0,9926992	0,9971653
126,9	1528,8	161,2
155,4	1702,2	170,5		МОБР
185,8	1899,5	181,5		79,150987	-46,02522	-32,67836
217,5	2127,6	195,4		-46,02522	203,40132	-157,1355
260,9	2368,5	217,4		-32,67837	-157,1355	190,12991
Частные коэффициены корреляции
r(Y,X1/X2)	r(Y,X2/X1)	r(X1,X2/Y)
0,362736	0,266383	0,799047

Рис. 4.5

Рис. 4.6

2) заполните диалоговое окно ввода данных и параметров вывода (рис.4.7):

Входной интервал – диапазон, содержащий анализируемые данные;

Группирование – переключатель, указывающий расположение данных по столбцам или по строкам;

Метки – флажок в этой позиции означает, что первая строка исходного диапазона содержит название столбцов;

Параметры вывода – активизируйте выходной интервал и укажите адрес левой верхней ячейки выходного диапазона.

Значения частных коэффициентов корреляции были рассчитаны по формуле (4.24), для этого была обращена матрица R (корреляция 1) при помощи функции МОБР.

Рис. 4.7

Выводы по задаче:

1) Из рисунка следует, что значения выборочных коэффициентов корреляции указывают на достаточно сильную корреляцию между факторами Х ₁, Х ₂ (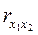 = 0,997) и частный коэффициент корреляции также высок ( = 0,799), следовательно в модели присутствует мультиколлинеарность. Кроме того det R = 0,0057, т.е. близок к нулю, и проверка с помощью - распределения показала, что (13,87) > (5,024), что также свидетельствует о наличии мультиколлинеарности. Здесь значение было рассчитано по формуле (4.22).

2) Из частных коэффициентов корреляции 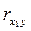= 0,363 и = 0,266 следует, что влияние Х ₁ на Y больше, чем Х ₂ на Y. Частные коэффициенты детерминации = ()²= 0,132 и = (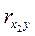)²= 0,071 показывают, что 13,2% рассеивания переменной Y обусловлено изменением только Х ₁, а 7,1% - Х ₂.

4.2.3. Проверка наличия автокорреляции

Эта проверка была произведена в Главе II. Если факт автокорреляции был зафиксирован, то здесь предлагается скорректировать уравнение множественной регрессии с помощью авторегрессионной схемы первого порядка, описанной в п. 4.1.4.

Вопросы для подготовки к защите индивидуального задания

1. Что такое гомоскедастичность и гетероскедастичность?

2. Приведите пример взаимоотношений в экономике, описываемых моделью с гетероскедастичными остатками.

3. Каким образом осуществляется проверка эконометрической модели на гомоскедастичность?

4. Почему нельзя применять классический МНК в случае гетероскедастичности?

5. Какие преобразования исходных данных нужно провести в случае обнаружения гетероскедастичности?

6. В чем суть метода взвешенных наименьших квадратов (ВМНК)?

7. Как вы понимаете термин «автокорреляция остатков»?

8. Приведите пример взаимоотношений в экономике, описываемых моделью с автокоррелированными остатками.

9. Каковы последствия применения классического МНК к модели с автокоррелированными остатками?

10. Каким образом осуществляется проверка эконометрической модели на автокорреляцию остатков?

11. Опишите схему использования статистики DW Дарбина-Уотсона.

12. Какие преобразования исходных данных нужно провести в случае обнаружения автокорреляции остатков?

13. Что такое мультиколлинеарность?

14. По каким проявлениям можно судить о наличии мультиколлинеарности в оцененной модели?

15. Каковы негативные последствия мультиколлинеарности?

16. Перечислите основные методы устранения мультиколлинеарности.

Глава V

Дата добавления: 2014-11-29