Распределение Дарбина-Уотсона 4 страница

СРЗНАЧ(число1; число2;...).

Возвращает среднее (арифметическое) своих аргументов.

Число1, число2,... - это от 1 до 30 аргументов, для которых вычисляется среднее.

СТАНДОТКЛОН(число1; число2;...).

Оценивает стандартное отклонение по выборке. Стандартное отклонение - это мера того, насколько широко разбросаны точки данных относительно их среднего.

Число1, число2,... - это от 1 до 30 числовых аргументов, соответствующих выборке из генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

ТЕНДЕНЦИЯ (известные_значения_ y;известные_значения_ x;новые значения_ x; конст).

Возвращает значения в соответствии с линейным трендом. Аппроксимирует прямой линией (по методу наименьших квадратов) массивы известные_значения_ y и известные_значения_ x. Возвращает значения y, в соответствии с этой прямой для заданного массива новые_значения_ x.

Известные_значения_ y - это множество значений y, которые уже известны для соотношения y = mx + b.

Известные_значения_ x - это необязательное множество значений x, которые уже известны для соотношения y = mx + b.

• Если известные_значения_x опущены, то предполагается, что это массив {1;2;3;...} такого же размера как и известные_значения_y.

Новые_значения_ x - это новые значения x, для которых ТЕНДЕНЦИЯ возвращает соответствующие значения y.

Конст - это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.

• Если конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом.
• Если конст имеет значение ЛОЖЬ, то b полагается равным 0, и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.

ХИ2ОБР(вероятность; степени_свободы).

Возвращает значение обратное к односторонней вероятности распределения γ2 (хи-квадрат). Если вероятность = ХИ2РАСП (x;...), то ХИ2ОБР (вероятность;...)= x. Функция используется для сравнения наблюдаемых результатов с ожидаемыми, для того, чтобы решить была ли исходная гипотеза обоснованной.

Вероятность - это вероятность, связанная с распределением γ2 (хи-квадрат).

Степени_свободы - это число степеней свободы.

МАТЕМАТИЧЕСКИЕ ФУНКЦИИ

СУММ (число1; число2;...).

Суммирует все числа в интервале ячеек.

Число1, число2,... - это от 1 до 30 аргументов, для которых требуется определить сумму.

СУММКВ (число1; число2;...).

Возвращает сумму квадратов аргументов.

Число1, число2,... - это от 1 до 30 аргументов, квадраты которых суммируются. Можно использовать отдельный массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

СУММКВРАЗН (массив_ x; массив_ y).

Возвращает сумму квадратов разностей соответствующих значений в двух массивах.

Массив_ x - это первый массив или интервал значений.

Массив_ y - это второй массив или интервал значений.

СУММПРОИЗВ (массив1; массив2; массив3;...).

Перемножает соответствующие элементы заданных массивов и возвращает сумму произведений.

Массив1, массив2, массив3,... - это от 2 до 30 массивов, чьи компоненты нужно перемножить, а затем сложить.

МОБР (массив).

Возвращает обратную матрицу для матрицы, хранящейся в массиве.

Массив - это числовой массив с равным количеством строк и столбцов.

МОПРЕД (массив).

Возвращает определитель матрицы (матрица хранится в массиве).

Массив - это числовой массив с равным количеством строк и столбцов.

МУМНОЖ (массив; массив2).

Возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив1 и с таким же числом столбцов, как массив2.

Массив1, массив2 - это перемножаемые массивы.

• Количество столбцов аргумента массив1 должно быть таким же, как количество сток аргумента массив2, и оба массива должны содержать только числа.

ССЫЛКИ И МАССИВЫ

ИНДЕКС (массив; номер_строки; номер_столбца).

Возвращает значение указанной ячейки или массив значений в аргументе массив.

ЧСТРОК (массив).

Возвращает количество строк в ссылке или массиве.

Массив - это массив, формула массива или ссылка на интервал ячеек, для которого определяется число строк.

ТРАНСП (массив).

Возвращает вертикальный диапазон ячеек в виде горизонтального и наоборот.

Массив — это транспонируемый массив или диапазон ячеек на рабочем листе. Транспонирование массива заключается в том, что первая строка массива становится первым столбцом нового массива, вторая строка массива становится вторым столбцом нового массива и так далее.

Приложение 2

Критические точки d ₁ и d _u при уровне значимости 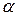= 0,05 (n – объем выборки, m – число факторов в уравнении регрессии)

n	m =1	m =2	m =3	m =4	m =5
d 1	d u	d 1	d u	d 1	d u	d 1	d u	d 1	d u
	0,61	1,40
	0,70	1,36	0,47	1,90
	0,76	1,33	0,36	1,78	0,37	2,29
	0,82	1,32	0,63	1,70	0,44	2,13	0,30	2,39
	0,88	1,32	0,70	1,64	0,53	2,02	0,38	2,41	0,24	2,82
	0,93	1,32	0,66	1,60	0,60	1,93	0,44	2,28	0,32	2,65
	0,97	1,33	0,81	1,58	0,66	1,86	0,51	2,18	0,38	2,51
	1,01	1,34	0,86	1,56	0,72	1,82	0,57	2,09	0,45	2,39
	1,05	1,33	0,91	1,55	0,77	1,78	0,63	2,03	0,51	2,30
	1,08	1,36	0,95	1,54	0,82	1,75	0,69	1,97	0,56	2,21
	1,1	1,37	0,98	1,54	0,86	1,73	0,74	1,93	0,62	2,15
	1,13	1,38	1,02	1,54	0,90	1,71	0,78	1,90	0,67	2,10
	1,16	1,39	1,05	1,53	0,93	1,69	0,82	1,87	0,71	2,06
	1,18	1,40	1,08	1,53	0,97	1,68	0,86	1,85	0,75	2,02
	1,20	1,41	1,10	1,54	1,00	1,68	0,90	1,83	0,79	1,99
	1,22	1,42	1,13	1,54	1,03	1,67	0,93	1,81	0,83	1,96
	1,24	1,43	1,15	1,54	1,05	1,66	0,96	1,80	0,86	1,94
	1,26	1,44	1,17	1,54	1,08	1,66	0,99	1,79	0,90	1,92
	1,27	1,45	1,19	1,55	1,10	1,66	1,01	1,78	0,93	1,90
	1,29	1,45	1,21	1,55	1,12	1,66	1,04	1,77	0,95	1,89
	1,30	1,46	1,22	1,55	1,14	1,65	1,06	1,76	0,98	1,88
	1,32	1,47	1,24	1,56	1,16	1,65	1,08	1,76	1,01	1,86
	1,33	1,48	1,26	1,56	1,18	1,65	1,10	1,75	1,03	1,85
	1,34	1,48	1,27	1,56	1,20	1,65	1,12	1,74	1,05	1,84
	1,35	1,49	1,28	1,57	1,21	1,65	1,14	1,74	1,07	1,83
	1,36	1,50	1,30	1,57	1,23	1,65	1,16	1,74	1,09	1,83
	1,37	1,50	1,31	1,57	1,24	1,65	1,18	1,73	1,11	1,82
	1,38	1,51	1,32	1,58	1,26	1,65	1,19	1,73	1,13	1,81
	1,39	1,51	1,33	1,58	1,27	1,65	1,21	1,73	1,15	1,81
	1,40	1,52	1,34	1,58	1,28	1,65	1,22	1,73	1,16	1,80
	1,41	1,52	1,36	1,59	1,29	1,65	1,24	1,73	1,18	1,80
	1,42	1,53	1,36	1,59	1,31	1,66	1,25	1,72	1,19	1,80
	1,43	1,54	1,37	1,59	1,32	1,66	1,26	1,72	1,21	1,79
	1,43	1,54	1,38	1,60	1,33	1,66	1,27	1,72	1,22	1,79
	1,44	1,54	1,39	1,60	1,34	1,66	1,29	1,72	1,23	1,79
	1,48	1,57	1,43	1,62	1,38	1,67	1,34	1,72	1,29	1,78
	1,50	1,59	1,46	1,63	1,42	1,67	1,38	1,72	1,34	1,77
	1,53	1,60	1,49	1,64	1,45	1,68	1,41	1,72	1,38	1,77
	1,55	1,62	1,51	1,65	1,48	1,69	1,44	1,73	1,41	1,77
	1,57	1,63	1,54	1,66	1,50	1,70	1.47	1,73	1,44	1,77
	1,58	1,64	1,55	1,67	1,52	1,70	1,49	1,74	1,46	1,77
	1,61	1,66	1,59	1,69	1,56	1,72	1,53	1,74	1,51	1,77

Критические точки d ₁ и d _u при уровне значимости 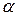= 0,01 (n – объем выборки, m – число факторов в уравнении регрессии)

n	m =1	m =2	m =3	m =4	m =5
d 1	d u	d 1	d u	d 1	d u	d 1	d u	d 1	d u
	0,39	1,14
	0,43	1,04	0,29	1,68
	0,50	1,00	0,34	1,49	0,23	2,10
	0,55	1,00	0,41	1,39	0,28	1,87	0,18	2,43
	0,60	1,00	0,47	1,33	0,34	1,73	0,23	2,19	0,13	2,69
	0,63	1,01	0,32	1,30	0,40	1,64	0,29	2,03	0.19	2,43
	0,70	1,02	0,37	1,27	0,45	1,37	0,34	1,91	0,24	2,28
	0,74	1,04	0,62	1,26	0,50	1,33	0,39	1,83	0,29	2,13
	0,78	1,03	0,66	1,23	0,35	1,49	0,44	1,74	0,34	2,05
	0,81	1,07	0,70	1,23	0,39	1,46	0,49	1,70	0,39	1,97
	0,84	1,09	0,74	1,23	0,63	1,45	0,33	1,66	0,44	1,90
	0,87	1,10	0,77	1,23	0,66	1,43	0,37	1,63	0,48	1,85
	0,90	1,12	0,80	1,24	0,71	1,42	0,61	1,60	0,32	1,80
	0,93	1,13	0,83	1,26	0,74	1,41	0,63	1,38	0,36	1,77
	0,93	1,15	0,86	1,27	0,77	1,41	0,68	1,37	0,40	1,74
	0,97	1,16	0,89	1,28	0,80	1,41	0,72	1,33	0,63	1,71
	1,00	1,17	0,91	1,28	0,83	1,41	0,75	1,34	0,67	1,70
	1,02	1,19	0,94	1,29	0,84	1,41	0,78	1,33	0,70	1,67
	1,04	1,20	0,96	1,30	0,88	1,41	0,80	1,33	0,73	1,64
	1,03	1,21	0,98	1,30	0,91	1,41	0,83	1,32	0,74	1,64
	1,07	1,22	1,00	1,31	0,93	1,41	0,83	1,32	0,78	1,63
	1,09	1,23	1,02	1,32	0,95	1,41	0,88	1,31	0,81	1,63
	1,10	1,24	1,04	1,32	0,97	1,41	0,90	1,31	0,83	1,62
	1,12	1,23	1,03	1,33	0,99	1,42	0,92	1,31	0,83	1,61
	1,13	1,26	1,07	1,34	1,00	1,42	0,94	1,31	0,88	1,61
	1,15	1,27	1,08	1,34	1,02	1,42	0,96	1,31	0,90	1,60
	1,16	1,28	1,10	1,33	1,04	1,43	0,98	1,31	0,92	1,40
	1,17	1,29	1,11	1,34	1,03	1,43	1,00	1,31	0,94	1,39
	1,18	1,30	1,13	1,36	1,07	1,43	1,01	1,31	0,93	1,39
	1,19	1,31	1,14	1,37	1,08	1,44	1,03	1,31	0,97	1,39
	1,21	1,31	1,13	1,38	1,10	1,44	1,04	1,31	0,99	1,39
	1,22	1,32	1,16	1,38	1,11	1,45	1,04	1,31	1,00	1,39
	1,23	1,33	1,18	1,39	1,12	1,45	1,07	1,31	1,02	1,38
	1,24	1,34	1,19	1,39	1,14	1,43	1,08	1,32	1,03	1,38
	1,25	1,34	1,20	1,40	1,15	1,44	1,10	1,32	1,05	1,38
	1,29	1,38	1,24	1,42	1,20	1,47	1,14	1,33	1,11	1,38
	1,32	1,40	1,28	1,45	1,24	1,49	1,20	1,34	1,16	1,39
	1,34	1,43	1,32	1,47	1,28	1,31	1,25	1,35	1,21	1,39
	1,38	1,45	1,33	1,48	1,32	1,32	1,28	1,34	1,25	1,40
	1,41	1,47	1,38	1,30	1,35	1,33	1,31	1,37	1,28	1,60
	1,43	1,48	1,40	1,31	1,37	1,35	1,34	1,38	1,31	1,61
	1,47	1,31	1,44	1,34	1,42	1,37	1,39	1,39	1,36	1,62

Приложение 3

Критические значения критерия Ирвина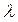

Число наблюдений n
Р = 0,95	Р = 0,99
	2,8	3,7
	2,2	2,9
	1,5	2,0
	1,3	1,8
	1,2	1,7
	1,1	1,6
	1,0	1,5
	0,9	1,3
	0,8	1,2

Дата добавления: 2014-11-29