КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнения при описании СУИМ
|
|
|
|
В инженерной практике для описания динамических дискретных звеньев СУИМ (объектов управления, регуляторов, фильтров и т.п.) применяют дискретные передаточные функции (ДПФ), записываемые в виде
 (9.9)
(9.9)
где X (z), Y (z) – соответственно входная и выходная переменные дискретного звена. Заметим, что практически реализуемые дискретные передаточные функции должны иметь порядок полинома знаменателя больше порядка полинома числителя.
Способы получения ДПФ:
1). Прямой способ (прямое дискретное преобразование Лапласа):
|
 x (t)
x (t) 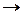 x (kT)
x (kT) 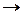 X (z)
X (z) 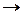
y (t) 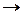 y (kT)
y (kT) 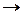 Y (z)
Y (z) 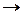
Чтобы получить прямое дискретное преобразование Лапласа сигнала x (t), необходимо заменить этот сигнал дискретными значениями x (kT). Каждое значение x (kT) домножить на z - k, а затем полученный степенной ряд свернуть в конечную сумму (9.7), которая по сути представляет собой дискретное преобразование Лапласа X (z). Аналогично получают прямое дискретное преобразование Лапласа сигнала y (t). Прямое Z -преобразование является однозначным преобразованием.
2). С помощью таблицы Z –преобразований [6-10]. Алгоритм получения ДПФ аналогичен рассмотренному выше, но не требует нахождения дискретных выборок входного x (kT) и выходного y (kT) сигналов.
3). Метод подстановки. На практике наиболее распространены два типа подстановок:
– метод прямоугольников (нуль-интерполяции):
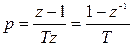 ; (9.10)
; (9.10)
– метод трапеций или метод Тастина (линейная интерполяция):
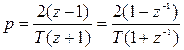 , (9.11)
, (9.11)
где T – такт квантования.
Метод трапеций обеспечивает более точную в отношении среднеквадратического критерия аппроксимацию непрерывных сигналов, как при их нарастании, так и спадании.
К ДПФ и соответствующим структурным схемам применимы те же правила структурных преобразований, что и для непрерывных систем.
Для синтеза систем управления реального времени, исследования цифровых систем управления во временной области используют разностные уравнения. Если известна дискретная передаточная функция какого-либо звена, то получение разностного уравнения не представляет труда. В частности, разностные уравнения, описывающие процессы в идеальных интегрирующих звеньях, аппроксимируемых методами нуль-интерполяции и линейной интерполяции, имеют соответственно вид: Y (kT) = Y ((k -1) T) + TX (kT);
Y (kT) = Y ((k -1) T) + 0,5 T [ X (kT) + X ((k -1) T)].
9.3. Синтез цифровых систем управления
Существует множество методов синтеза цифровых систем управления,
основанных на описании управляемых динамических процессов, как в частотной, так и во временной области [6,10,16,23,24].
Для синтеза цифровых СУИМ применяют, в частности:
– метод дискретизации по времени аналоговых регуляторов класса “вход/выход” (метод аналогий) или метод билинейного преобразования;
– метод переменного коэффициента усиления;
– методы аналитического конструирования дискретных регуляторов состояния.
9.3.1. Методы дискретизации аналоговых регуляторов
и билинейного преобразования
Метод дискретизации основан на применении рассмотренных выше процедур синтеза линейных аналоговых СУИМ. В качестве критериев оптимальности принимают общепринятые при синтезе таких систем интегральные квадратичные или иные функционалы, а, следовательно, динамические процессы в оптимизированных контурах регулирования соответствуют реакциям тех или иных оптимальных фильтров, например фильтров Баттерворта n -го порядка, апериодических фильтров и т.п. В одноконтурных и системах подчиненного регулирования координат СУИМ синтезированное аналоговое устройство управления содержит один или несколько последовательно включенных регуляторов (корректирующих устройств) класса “вход/выход”.
Для преобразования аналоговых передаточных функций регуляторов в дискретные передаточные функции применяют замену непрерывных операторов p Лапласа их дискретным аналогом, используя метод прямоугольников (в классической теории управления непрерывными системами – метод Эйлера). Отсюда и второе название данного метода синтеза – метод аналогий.
В качестве примера рассмотрим дискретизацию непрерывного ПИД-закона регулирования. Процедура преобразования иллюстрируется рис. 9.4.
Входным воздействием регулятора является ошибка регулирования e (t) для непрерывного и e (kT) для дискретного управления, выходным сигналом – сигнал u (t) для непрерывного и u (kT) для дискретного управления.
 |
Приведенное преобразование основано на замене (9.10):
Рис. 9.4. Иллюстрация метода дискретизации аналогового ПИД-регулятора
Метод билинейного преобразователя – по сути, тот же метод аналогий, но он сводится к применению подстановки (9.11). Такую подстановку целесообразно применять к интегральной компоненте управления (звену 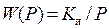 ), поскольку именно она отвечает за точность управления.
), поскольку именно она отвечает за точность управления.
Параметры К рег, К и, К Д получены в результате синтеза аналогового ПИД- регулятора, Т – временной интервал между двумя соседними значениями управляющего воздействия (такт управления).
Применение этих методов синтеза предполагает, что дискретизацией аналоговых сигналов по уровню в силу достаточной длины разрядной сетки цифровых средств управления можно пренебречь, такт управления достаточно мал (как правило, на порядок меньше минимальной постоянной времени объекта управления). Также предполагается, что периоды Т прерывания импульсного элемента датчиков обратной связи и регуляторов одинаковы и неизменны, причем синхронизированы во времени. Как показывают исследования [15,16,23,24], в цифровых электромеханических СУИМ такт прерывания не должен превышать 0,005 с. Обеспечение этих условий позволяет получить динамические характеристики цифровой СУИМ практически такие же, что и в непрерывной системе.
9.3.2. Метод переменного коэффициента усиления
В основе метода лежат теорема об n интервалах дискретного управления и применение дискретных уравнений переходных состояний [6,10]. Дискретный регулятор на начальном этапе синтеза представляется в виде последовательной цепочки, состоящей из квантователя ошибки e (t) регулирования по времени с тактом T, фиксатора Ф нулевого порядка и безынерционного звена с переменным коэффициентом Кj усиления (рис. 9.5).
 |
Рис. 9.5. Структура дискретного регулятора на начальном этапе синтеза
Входным воздействием регулятора является ошибка регулирования
e (kT), выходным – сигнал управления u (kT). Ошибка регулирования e (kT) на входе звена с переменным коэффициентом усиления обновляется и фиксируется с помощью экстраполятора нулевого порядка с каждым тактом дискретизации Т.
Согласно теореме об n интервалах дискретного управления система будет оптимальной по быстродействию (в концепции импульсных САУ), если переходные процессы в ней заканчиваются через n тактов управления, причем без перерегулирования выходной координаты, где n – порядок линейного объекта управления. Критерий оптимальности системы (максимум быстродействия) в этом случае записывается в виде t рег = nT 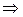 min. Цель синтеза – определение n значений коэффициента Кj, обеспечивающих достижение предельного быстродействия СУИМ.
min. Цель синтеза – определение n значений коэффициента Кj, обеспечивающих достижение предельного быстродействия СУИМ.
Для дискретной СУИМ с рассматриваемым регулятором можно записать n дискретных уравнений переходных состояний
 (9.12)
(9.12)
где V [(k -1) T ] – вектор состояния системы на предыдущем такте управления;
 – вектор состояния на текущем такте управления после замыкания ключевых элементов (фиксации новых значений измеренной координаты и ошибки регулирования);
– вектор состояния на текущем такте управления после замыкания ключевых элементов (фиксации новых значений измеренной координаты и ошибки регулирования);
Ф (Кj, Т) – расширенная матрица перехода системы, зависящая от искомых коэффициентов Кj;
B (T) – матрица переключения импульсных элементов.
В результате решения системы n неоднородных алгебраических уравнений, составленных из дискретных уравнений состояний, находят численные значения коэффициентов Кj. Для этого применяют различные методики, алгоритмы и численные процедуры [6,10].
На заключительном этапе синтеза оптимальный регулятор представляют в виде дискретной передаточной функции
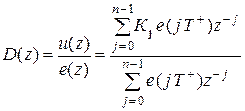 . (9.12)
. (9.12)
В отличие от рассмотренного ранее метода синтеза такт управления здесь выбирается исходя из ограничений ресурсов управления (чем меньше требуемое время регулирования, тем большими ресурсами управления должна обладать САУ). В частности, для цифровых электромеханических СУИМ в зависимости от регулируемой координаты значение Т находится в пределах 0,01…0,05 с, что позволяет применить для управления микропроцессорный контроллер с достаточно малым быстродействием.
К существенным недостаткам метода следует отнести довольно высокую чувствительность синтезированных СУИМ к вариациям параметров объекта управления к “чужим” аддитивным воздействиям. Например, система, оптимизированная по критерию быстродействия по задающим воздействиям, может оказаться далеко не оптимальной в смысле этого критерия при отработке возмущающих воздействий. Кроме того, регулирование по отклонению e (t) (ошибке регулирования) не гарантирует необходимой динамической точности регулирования при изменении вида задающего воздействия, отличного от принятого при процедуре синтеза. В итоге система оказывается малопригодной при программно-временном и следящем управлении.
9.3.3. Метод аналитического конструирования цифровых
регуляторов состояния
Многие системы управления относятся к классу систем, функционирующих в режимах малых отклонений координат: систем стабилизации той или иной технологической координаты (скорости вращения или перемещения рабочего органа, температуры, давления, натяжения и т.п.), следящих систем управления, систем воспроизведения движений. Поскольку основным технологическим требованием при синтезе таких систем является максимальное быстродействие и минимум динамической ошибки отработки рассогласований заданных и действительных значений координат состояния, в качестве дискретного критерия оптимальности часто принимают критерий вида 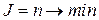 , где
, где 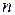 – число периодов дискретного управления, по истечении которых система приходит в установившееся состояние без перерегулирования выходной переменной [6,10].
– число периодов дискретного управления, по истечении которых система приходит в установившееся состояние без перерегулирования выходной переменной [6,10].
Синтез апериодических динамических систем, а именно такими являются системы, гарантирующие отсутствие перерегулирования в замкнутых дискретных САУ, традиционно проводят на основе идеальной компенсации нулей и полюсов объекта управления полюсами и нулями дискретной передаточной функции регулятора, а также добавления новых полюсов и нулей в соответствующих областях Z - плоскости [6,23]. Неточность математического описания, временной и температурный дрейф параметров объекта управления, ограничения в реализации передаточной функции регулятора техническими средствами приводят к неустойчивости замкнутой системы. Более того, такая процедура синтеза СУИМ даже при идеальной компенсации полюсов и нулей предполагает “апериодичность” переходных процессов только по отношению к входным воздействиям определенного вида и места их приложения. По отношению к “чужим” входным воздействиям система может иметь неприемлемое качество. В этой связи синтез СУИМ осуществляют на основе контроля полного состояния системы и реализации апериодических регуляторов состояния.
Ниже рассмотрена аналитическая процедура синтеза апериодических регуляторов состояния, обеспечивающих апериодические переходные процессы в линейных системах произвольного порядка. Предлагаемая процедура синтеза теоретически обеспечивает в системе управления астатизм первого порядка по задающим воздействиям, а, следовательно, повышенную точность отработки изменяющихся во времени задающих воздействий.
Пусть линейный стационарный объект управления описывается дискретно-непрерывным векторно-матричным уравнением
 , (9.13)
, (9.13)
где  – векторы состояния, управления и возмущения соответственно размерности
– векторы состояния, управления и возмущения соответственно размерности 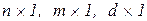 ;
;
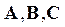 – матрицы состояния, управления, возмущения размерности
– матрицы состояния, управления, возмущения размерности  соответственно;
соответственно;
T – такт дискретного управления;
k – номер такта дискретного управления.
Задача синтеза формулируется следующим образом: необходимо для произвольных начальных значений  и постоянного на интервале nT вектора возмущений F( t) сформировать дискретную управляющую последовательность (U kT), k= 0,1,...,переводящую объект управления (9.13) в заданное конечное состояние
и постоянного на интервале nT вектора возмущений F( t) сформировать дискретную управляющую последовательность (U kT), k= 0,1,...,переводящую объект управления (9.13) в заданное конечное состояние 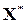 за n тактов управления, где n – порядок динамического объекта. Допущения при синтезе оптимального управления: время измерения координат состояния и выработки (вычисления) координаты управления ничтожно мало в сравнении с тактом T управления; длина разрядной сетки ЭВМ и устройств связи с объектом управления позволяет пренебречь квантованием непрерывных сигналов по уровню; значение периода управления T предполагается априори выбранным исходя из ограничений ресурсов управления. Приведенные допущения являются широко распространенными при синтезе дискретных систем управления объектами рассматриваемого класса [6].
за n тактов управления, где n – порядок динамического объекта. Допущения при синтезе оптимального управления: время измерения координат состояния и выработки (вычисления) координаты управления ничтожно мало в сравнении с тактом T управления; длина разрядной сетки ЭВМ и устройств связи с объектом управления позволяет пренебречь квантованием непрерывных сигналов по уровню; значение периода управления T предполагается априори выбранным исходя из ограничений ресурсов управления. Приведенные допущения являются широко распространенными при синтезе дискретных систем управления объектами рассматриваемого класса [6].
Представим искомую управляющую дискретную последовательность в виде линейной формы дискретных значений векторов состояния X (kT), задающих воздействий X *(kT), вектора возмущения F (kT) и вектора производных задающих воздействий  в виде
в виде
 . (9.14)
. (9.14)
В этом уравнении 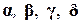 – матрицы соответственно размерности
– матрицы соответственно размерности 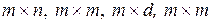 , определение которых и является задачей синтеза.
, определение которых и является задачей синтеза.
Предлагаемый подход основан на разных формах представления объекта управления (в виде непрерывной модели) и устройства управления (в виде дискретной модели), причем структура устройства управления предполагается заданной не в виде дискретной передаточной функции, а в виде линейного дискретного регулятора состояния системы.
Векторная структурная схема такой дискретно-непрерывной системы приведена на рис. 9.6.
Пунктирными линиями на схеме выделены объект управления (ОУ) и устройство управления (УУ) - дискретный регулятор состояния. Дискретизация вектора управления и, соответственно, всех аддитивных воздействий осуществляется в моменты времени kT (k = 0, 1, 2, …) методом интерполяции нулевого порядка. Экстраполятор (фиксатор) нулевого порядка обозначен на схеме аббревиатурой ЭНП. Простейшая аппаратная реализация векторного ЭНП - m устройств выборки-хранения, имеющих общий квантователь сигналов в моменты времени kT (m – размерность вектора управления). При микропроцессорной реализации дискретного регулятора состояния ЭНП – совокупность регистров памяти с перезаписью информации с тактом T управления.
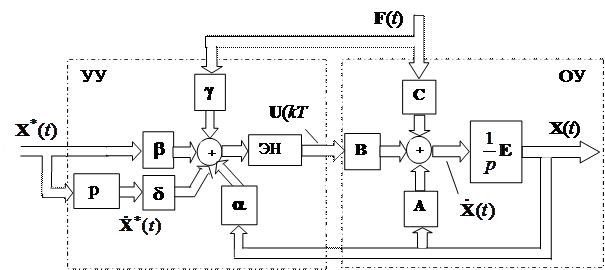 |
Рис. 9.6. Векторная структурная схема дискретно-непрерывной САУ
Заметим, что линейность моделей (9.13) объекта управления и регулятора (9.14) состояния объекта управления позволяет при синтезе САУ применить принцип суперпозиции управляемых динамических процессов. Проведем декомпозицию управляющей дискретной последовательности и динамических процессов в системе на две составляющие – управляемый свободный процесс и управляемый вынужденный процесс. В соответствие с этим в процедуре синтеза выделим два этапа – синтез свободного и синтез вынужденного движений.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 913; Нарушение авторских прав?; Мы поможем в написании вашей работы!