Синтез свободного движения САУ

Управляемый свободный процесс в системе определяется парой матриц A, B объекта управления и матрицей регулятора состояния, призванной обеспечивать оптимальность переходных свободных движений при произвольных начальных значениях вектора состояния X (0). На первом этапе синтеза будем полагать равными нулю все внешние аддитивные воздействия . Тогда управление свободным движением примет вид

(9.15)

Для нахождения матрицы воспользуемся теоремой об n интервалах дискретного управления в сочетании с принципом оптимальности Беллмана [10]. Не снижая общности выкладок, будем полагать, что оптимальное свободное движение системы завершается через n тактов дискретного управления в нулевой точке пространства состояний . Сформируем расширенный вектор-столбец состояния

V (t) = col [ X (t), U (kT)] (9.16)

и перепишем уравнение для случая управляемого свободного движения в виде

(9.17)

где D – матрица управляемого состояния размерности (n+m)´(n+m),

. (9.18)

Зададимся некоторой произвольной дискретной управляющей последовательностью U (kT), k = –1, –2,..., – n и рассмотрим движение системы в обратном времени, т.е. примем конечное нулевое состояние системы за начальное. Проинтегрируем уравнение (9.17) при нулевых начальных условиях X (0) = 0, воспользовавшись аппаратом переходных матриц состояния, получим векторное дискретное уравнение состояния

(9.19)

где – расширенная обратная матрица перехода.

Сформируем матрицы дискретного управления W размерности и дискретного состояния G размерности 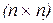в виде

W = [ U(- T) U(-2 T)... U(- nT) ], (9.20)

G = [ X(- T) X(-2 T)... X(- nT) ]. (9.21)

Поскольку не наложены какие-либо ограничения на множества управляющих воздействий и дискретные состояния системы, а также, по определению, система находилась в нулевом начальном состоянии, очевидно, что ее движение в обратном (по отношению к принятому при синтезе) направлении будет носить оптимальный по быстродействию апериодический характер. Следовательно, с учетом выражения (9.15) искомую матрицу можно найти в виде

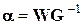. (9.22)

Решение векторно-матричного уравнения (9.22) будет единственным при полном ранге матрицы G,т.е. если rank (G) = n.

Дата добавления: 2014-11-29