Заміна змінної у визначеному інтегралі

При вивченні невизначеного інтеграла ми розглянули один з найбільш ефективних методів інтегрування функцій ― метод підстановки. Цим методом користуються також при обчисленні визначених інтегралів. Проте для визначеного інтеграла треба цей метод обґрунтувати. Доведемо таку теорему.

Теорема. Нехай виконуються умови:

1) 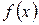неперервна функція на відрізку ;

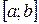2) функція 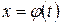і її похідна 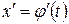неперервні на відрізку ;

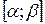3) 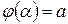, 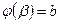і значення функції 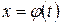не виходять за межі відрізка 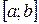при .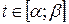

Тоді справджується рівність 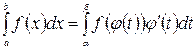(19)

Доведення. Спочатку зазначимо, що в обох частинах рівності (19) інтеграли існують, бо підінтегральні функції неперервні на відповідних відрізках. Введемо допоміжні функції

; ;

; .

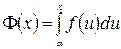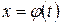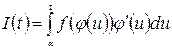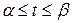Легко бачити, що 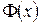і 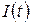мають похідні по 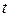, знайдемо їх. Функція 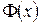є складеною. Продиференціюємо її:

.

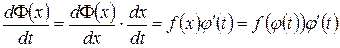Аналогічно .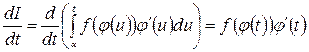

Отже, похідні функцій 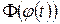і 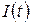рівні між собою, тому функції відрізняються одна від одної на сталу величину

.

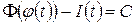Ця рівність справджується для будь-якого 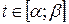. Нехай 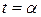. Маємо

.

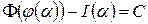Як бачимо, 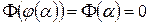, 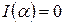. Отже, 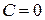. Тому .

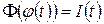Поклавши тут 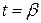і врахувавши, що , дістанемо формулу (19). Теорему доведено.

Зауваження. Якщо при знаходженні невизначеного інтеграла методом підстановки у первісній функції ми від змінної 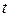поверталися до змінної 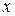(робили підстановку 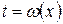), то при обчисленні визначеного інтеграла робити таку заміну немає потреби. Якщо вдається обчислити інтеграл, який міститься у правій частині формули (19), то цим самим обчислено і інтеграл лівої частини формули (19). На практиці, як і при знаходженні невизначеного інтеграла, найчастіше користуються підстановками виду 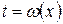. При цьому функція 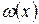повинна задовольняти умовам: 1) 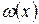має на відрізку 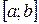неперервну похідну; 2) на відрізку 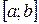вона є строго монотонною. Тоді така функція має обернену функцію 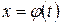, тобто маємо підстановку, про яку йдеться в теоремі. При цьому межі для 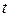знаходяться з рівності 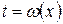. Тоді 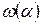є нижня межа по 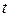, а 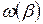― верхня межа.

Розглянемо окремий випадок формули (19), а саме, нехай маємо визначений інтеграл 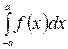, який можна записати так:

.

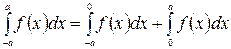У першому інтегралі застосовуємо поправку .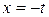

Очевидно, функція 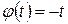на відрізку 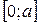задовольняє умови попередньої теореми. Отже,

.

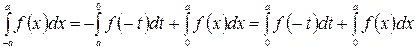Визначений інтеграл не залежить від того, якою буквою позначимо змінну інтегрування, тому в першому інтегралі замість 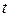візьмемо 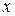. Матимемо

.

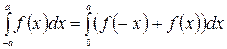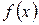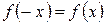Припустимо, що функція на відрізку є парною, тобто . Тоді з попередньої рівності дістаємо 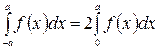. (20)

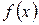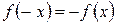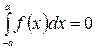Якщо на відрізку є непарною, , то .(21)

Дата добавления: 2014-11-29