Системный анализ информационно-управляющих комплексов

Состояние информационно-управляющих комплексов может быть представлено графом состояния системы. По графу системы можно судить о наличии или отсутствии стационарного режима.

Если число состояний конечно и из каждого состояния графа можно перейти за то или иное шагов в любое другое, то существует стационарный предельный режим системы.

а) б)

Рис. 4.12 Графы состояний системы.

а) в случае наличия стационарного режима;

б) в случае отсутствия стационарного режима.

При существовании предельного стационарного режима система случайным образом меняет свои состояния, но вероятность каждого из них уже не зависит от времени. Каждое из состояний осуществляется с некоторой постоянной вероятностью, представляющее собой не что иное, как среднее относительное время пребывания системы в данном состоянии.

Система дифференциальных уравнений вероятностей состояния комплекса переходит в стационарном режиме в систему линейных алгебраических уравнений, решение которой с учетом того что сумма вероятностей состояний комплекса P_j равна единице позволяет вычислить все предельные вероятности состояния P_j. С помощью этой методики можно решить ряд важных практических задач системного анализа информационно–управляющих комплексов.

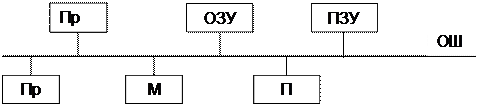Рассмотрим применение изложенного выше подхода на следующем примере. Исследуем влияние параметров программ на характеристики обмена информации в двухпроцессорном информационно-управляющем комплексе, структура которого имеет вид:

Рис. 4. 13. Структура информационно-управляющего комплекса.

Обозначения на рис. 4. 13.

Пр – процессоры;

ОЗУ – оперативное запоминающее устройство;

ПЗУ – постоянное запоминающее устройство;

М – монитор;

П – принтер.

В случае совместной работы двух процессоров и наличии одной магистрали при обмене командной и числовой информацией между процессорами, ОЗУ, ПЗУ будут, естественно, возникать конфликтные ситуации, когда оба процессора нуждаются в проведении обмена (ввод или вывод соответствующей информации). Если разрешение данного конфликта производится в пользу процессора первым обратившегося к магистрали, то второй будет находиться в состоянии ожидания ее освобождения. Причем время вынужденных простоев процессоров будет зависеть от временных характеристик программ. Чем больше длительность фазы автономной работы процессоров по сравнению с длительностью обмена в магистрали, тем меньше сказываются простои процессоров, тем выше производительность всего комплекса в целом.

Задачей системного анализа является исследование зависимости коэффициента загрузки магистрали h и коэффициента удлинения программ S для данной структуры комплекса от временных характеристик программ и пропускной способности магистрали.

Динамика системы отражается в изменении состояний процессоров. Каждый из процессоров может находиться в трех состояниях: O-работа; 1- обмен; 2- ожидание обмена. В соответствии с этим можно определить следующую совокупность состояний системы: (0; 0)- оба процессора работают; (1;0)- первый процессор в состоянии обмена, второй - в состоянии работы; (0;1)-первый процессор в состоянии работы, второй-В состоянии обмена, (1; 2) – первый процессор в состоянии обмена, второй – в ожидании обмена; (2;1) –первый процессор в состоянии ожидания обмена. Второй – в состоянии обмена.

Граф отражающий динамикусистемы, представлен на рис. 4. 14.

Рис. 4. 14. Граф состояний информационно-управляющего комплекса.

Длительность автономной фазы работы процессоров и длительность фазы их обмена являются случайными величинами, распределенными по показательному закону с параметрами l_i, m_i (i=1,2)

;

, (4. 42)

где – длительной фазы автономной работы i-го процессора; 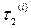–длительность фазы обмена i-го процессора с памятью (i=1;2).

Как видно из графа состояний системы, стационарный режим существует и соответствующая система уравнений для него будет:

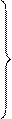-(l₁+l₂)P₀₀+m₁P₁₀+m₂P₀₁=0

-(l₂₊m₁)P₁₀+l₁P₀₀+m₂P₂₁=0

-(l₁+m₂)P₀₁+l₂P₀₀+m₁P₁₂=0 (4. 43)

l₂P₁₀-m₁P₁₂=0

l₁P₀₁-m₂P₂₁=0

Решая эту систему с учетом нормирующего уравнения получим неизвестные вероятности состояния и интересующие нас характеристики комплекса:

Коэффициент загрузки магистрали:

h=1-P₀₀ (4. 44)

Коэффициент удлинения первой программы:

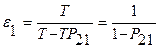, (4.45)

где T-общее время работы комплекса.

Коэффициент удлинения второй программы

(4.46)

Данные выражения позволяют сделать выводы об эффективности применения информационно-управляющего комплекса для решения выбранных задач обработки информации.

Дата добавления: 2014-11-29