Понятие о линейных, нелинейных и линеаризованных моделях

Для любого физического объекта может быть составлена математическая модель, которая представляет собой набор определенных математических соотношений между переменными величинами этого объект. Если в модели все соотношения между переменными линейны, то модель будет линейной. Примерами линейных соотношений являются уравнения

, , ,

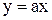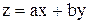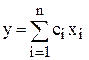где x, y, z – переменные величины; а, в, c – коэффициенты не зависящие от переменных величин.

Если среди соотношений модели появляется хотя бы одно нелинейное, модель становится нелинейной. Причинами нелинейности могут стать любые нелинейные операции над переменными или между переменными, а также над их производными, интегралами и т.д. К нелинейным операциям относятся умножение, деление, тригонометрические операции и многие другие. Примерами нелинейных соотношений между переменными являются уравнения

, , .

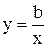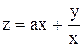При математическом моделировании технических объектов часто вводится деление причин нелинейности на две группы: либо в объекте выделяются элементы с нелинейными характеристиками, либо в уравнениях модели определяются нелинейные математические операции. Условность этого деления очевидна. Например, нелинейное уравнение 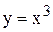, можно записать, как 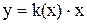, а можно записать, как 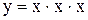. В первом случае говорят об элементе с нелинейной характеристикой 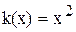, а во втором об элементе с тремя входными воздействиями, которые в элементе перемножаются (рис.1.2).

Рис. 1.2

Хорошо разработанный аналитический аппарат решения линейных дифференциальных уравнений делает крайне желательным применение линейных моделей. Поэтому для максимального использования ресурсов линейного моделирования используются специальные методы, которые позволяют превращать многие нелинейные модели в линейные. Эту процедуру называют линеаризацией.

Техника линеаризации. Линеаризация заключается в замене нелинейных уравнений приближенными линейными на основании предположения, что при небольших изменениях переменных величин параметры исследуемой системы остаются постоянными. Для выполнения линеаризации вводят понятие “точки линеаризации”, понимая под этим определенный стационарный режим работы системы, в окрестности которого будет исследоваться система. Значения параметров этого режима обозначают индексом «0».

Линеаризация нелинейной функции f(x₁,…,x_n)основана на использовании аффинной части ряда Тейлора, записанного для точки линеаризации 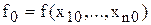. Ряд Тейлора для этой функции имеет вид:

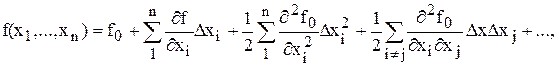(1.1)

а его аффинная часть

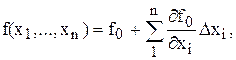(1.2)

где через 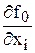обозначается частная производная функции f по аргументу x_i в точке линеаризации (x₁₀,…,x_n0). После переноса f₀в левую часть получаем линеаризованное выражение для исходной функции

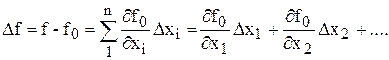(1.3)

Резюме. Линеаризованная функция записывается относительно приращений переменных исходной функции, то есть линеаризованная функция определяет значение не самой функции, а только ее приращения в точке линеаризации. Линеаризация уравнений и запись их в приращениях позволяют получить н у л е в ы е начальные условия.

В качестве примеров линеаризации рассмотрим следующие нелинейные уравнения 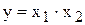, , . Пользуясь формулой (1.3), получим для них

,

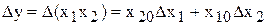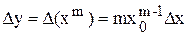, (1.4)

.

Рис. 1.3

Рис. 1.3

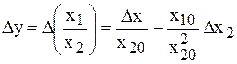Любую ли функцию можно линеаризовать указанным выше способом? Оказывается, нет. Из предыдущих рассуждений видно, что линеаризуется только такая функция, которая дифференцируема в окрестности точки линеаризации, то есть сама она и ее производные не терпят разрывов. Например, функцию, изображенную на рис.1.3, в окрестностях значений х₁ и х₂ линеаризовать нельзя. Кроме этого, производя линеаризацию этой функции в точках, где нет разрывов, необходимо позаботиться о том, чтобы при изменении переменной х ее значение не становилось равным х₁ или х₂. В противном случае линеаризация становится неправомерной, так как приводит к недопустимо большим ошибкам, которые даже трудно будет оценить.

При наличии существенных нелинейностей в системе (зон нечувствительности элементов, гистерезиса, участков полного насыщения и др.) ее динамические режимы исследуются специальными методами (фазовых траекторий, точечных преобразований, гармонического баланса и др.).

Пример 1.1. Линеаризовать функцию 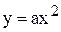в точке .

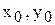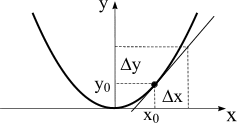Решение. Согласно формулы (1.1) для исходной функции запишем 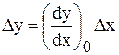. Учитывая, что 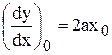, окончательно получим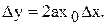

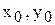Рис. 1.4

Рис. 1.4

Геометрическая иллюстрация этого результата на рис.1.4 показывает, что при линеаризации исходная нелинейная функция заменяется касательной, которая проходит через точку линеаризации . Из этого рисунка видно, также, что ошибка при линеаризации растет при отклонении переменной x от значения .

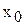Пример 1.2. Линеаризовать уравнение 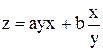в точке x₀,y_0.

Решение. Здесь можно воспользоваться как формулой (1.3), так и готовой формулой в (1.4). В результате получаем

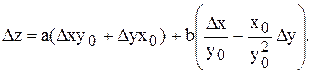
Дата добавления: 2014-11-29