Критерии устойчивости

Все критерии устойчивости делятся на алгебраические и частотные. Если для работы с алгебраическими критериями необходимо иметь, по крайней мере, характеристическое уравнение системы, то при использовании частотных критериев не обязательно иметь даже характеристическое уравнение, так как устойчивость может быть определена по экспериментальным характеристикам. Это свойство частотных критериев широко используется в практике работы со сложными системами, такими, например, как энергетические системы, когда построение математической модели затруднено. К алгебраическим критериям относятся критерии Гурвица и Рауса, к частотным - критерии Найквиста и Михайлова.

Критерий Гурвица. Проверка устойчивости по Гурвицу сводится к вычислению n определителей, которые составляются по следующему правилу:

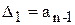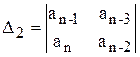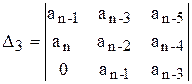; ; ;... (6.7)

По этому критерию система будет устойчивой, если все определители положительные.

Критерий Михайлова. Если в характеристическом уравнении системы заменим оператор p на jw, получим функцию комплексного переменного

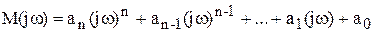, 6.8)

которая в комплексной плоскости определяет вектор

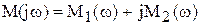. (6.9)

Этот вектор имеет следующее свойство. При изменении w от 0 до 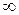этот вектор будет поворачиваться около начала координат против часовой стрелки, меняя одновременно и свою длину. При этом конец вектора описывает кривую со следующими свойствами: кривая начинается на вещественной оси при 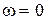в точке с координатой 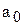и заканчивается в n-ом квадранте при 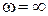, если отчет квадрантов вести против часовой стрелки. Этот вектор называют годографом Михайлова.

Согласно этому критерию линейная система n-го порядка будет устойчива, если годограф Михайлова охватывает начало координат и последовательно проходит n квадрантов, а в последнем квадранте уходит в бесконечность. Если годограф проходит через 0, то система находится на границе устойчивости.

б)

а)

На рис. 6.3,а изображены годографы устойчивых систем с характеристическими уравнениями до пятой степени включительно. А на рис. 6.3,б приведены годографы неустойчивых систем.

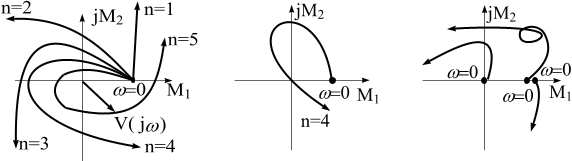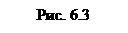Критерий Найквиста. Этот критерий позволяет определить устойчивость системы по ее амплитудно-фазовым характеристикам, которые могут быть заданы как в аналитической форме, так и в виде опытных кривых. Особенностью критерия является то, что оценка устойчивости системы делается по характеристикам ее разомкнутого состояния. Это оказывается возможным благодаря однозначной зависимости между передаточной функцией разомкнутой системы и характеристическим уравнением этой системы в замкнутом состоянии.

Исследуемая система размыкается в любой точке, и аналитически или экспериментально определяется ее АФХ. Эта характеристика представляется комплексным уравнением 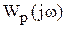. Устойчивость замкнутой системы определяется так:

1) если разомкнутая система устойчива или нейтральна, то для устойчивости замкнутой системы необходимо и достаточно, чтобы характеристика 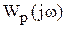не охватывала точку с координатами (-1, j0);

2) если разомкнутая система имеет m корней с положительной вещественной частью, то замкнутая система будет устойчивой только в том случае, если характеристика 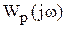охватывает точку (-1, j0) в положительном направлении 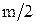раз.

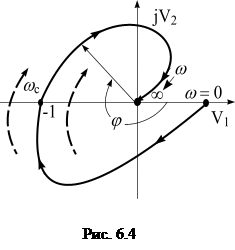Физическое объяснение этих условий можно дать с помощью рис. 6.4. Пусть при некоторой частоте 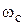система, находится на границе устойчивости. Это означает, что АФХ разомкнутой системы при этой частоте проходит через точку(-1, j0). Это означает также, что на данной частоте амплитуда выходного сигнала равна амплитуде входного сигнала, и они находятся в противофазе. Значит в замкнутой системе сигнал с выхода по цепи отрицательной обратной связи поступит на вход и будет точно равен по амплитуде и фазе входному сигналу. Если такую систему отключить от входного сигнала, ее состояние не изменится. В системе установятся незатухающие колебания, которые будут поддерживаться не за счет источника входного сигнала (он теперь отключен), а за счет энергии самой системы.

Если АФХ при частоте 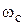пересекает вещественную ось слева от точки (-1, j0), то есть охватывает эту точку, то амплитуда выходного сигнала на данной частоте больше входного и находится в противофазе. При замыкании системы амплитуда выходных колебаний будет возрастать, то есть система будет неустойчивой.

Если АФХ при частоте 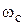пересекает вещественную ось справа от точки

(-1, j0), то есть не охватывает ее, то амплитуда выходного сигнала на данной частоте меньше входного и находится в противофазе. В этом случае при замыкании системы амплитуда выходных колебаний будет затухать, то есть система будет устойчивой.

6.5. Определение областей устойчивости. D – разбиение

Постановка задачи. Выше были рассмотрены принципы исследования системы на устойчивость при условии, что все ее параметры уже заданы. Но часто при проектировании и наладке автоматических систем предоставляется свобода в выборе некоторых ее параметров. При этом представляет интерес такая технология выбора параметров, при которой обеспечивался бы необходимый запас устойчивости. Эта задача решается посредством выделения областей устойчивости в плоскости выбираемых параметров. Поясним физический смысл этих областей.

Положим, что автоматическая система имеет характеристическое уравнение

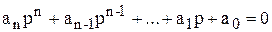. (6.10)

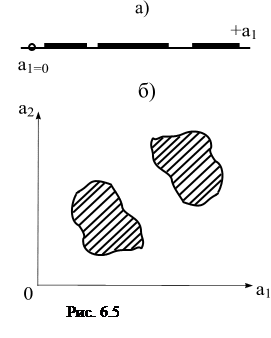Допустим сначала, что все коэффициенты, кроме одного, например, a₁, в этом уравнении заданы. Будем изменять этот коэффициент от 0 до Ґ и следить за расположением корней в комплексной плоскости. Каждое значение а₁на рис. 6.5,а отметим точкой, причем жирную точку ставим, когда при данном a₁ корни расположены слева от мнимой оси (система устойчива) и обычную точку когда расположение корней соответствует неустойчивой системе. Понятно, что ось значений a₁будет разбита на отрезки. Стыки этих отрезков есть границы устойчивости.

Положим теперь, что в уравнении (6.10) изменяются два коэффициента, например, 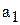и 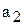, а остальные остаются неизменными. Тогда вся плоскость будет разбита на области устойчивости и неустойчивости. (На рис.6.5,б области устойчивости заштрихованы.) Выделяя в уравнении (6.10) три, четыре или большее количество свободных коэффициентов, будем получать области устойчивости соответственно в виде объемного пространства или гиперпространств. Разбиение пространства коэффициентов на области устойчивости называется D-разбиением.

Обычно в практических задачах почти все параметры системы конструктивно заданы, и свобода выбора остается за одним или двумя параметрами. Поэтому задача выделения областей устойчивости практически сводится к построению границы в плоскости одного или двух параметров.

Алгоритм D-разбиенийоснован на использовании годографа Михайлова, который соответствует границе устойчивости, то есть годограф проходящий через начало координат.

D-разбиение по одному параметру. Представим характеристическое уравнение системы в виде

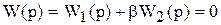, (6.11)

где b - свободный параметр, а 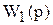и 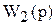– части характеристического уравнения, не содержащие параметр b. Заменим в этом уравнении р на jw и решим от-носительно b

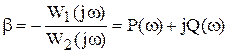. 6.12)

Кривая, построенная в системе координат Р(w), jQ(w) при различных значениях w, будет представлять границу D-разбиений. Область устойчивости находится слева от кривой, если двигаться по ней от значений 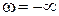к значению 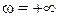. Границу области устойчивости обычно отмечают штриховкой.

Так как параметр b является вещественным числом, то нас интересует отрезок только вещественной оси, попадающий в область устойчивости. Все значения параметра, определяемые координатами этого отрезка на оси абсцисс, окаймлённого штриховкой, будут соответствовать устойчивому состоянию системы.

Пример 6.1. Рассмотрим систему регулирования с характеристическим уравнением

.

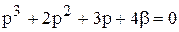Решим характеристическое уравнение относительно b

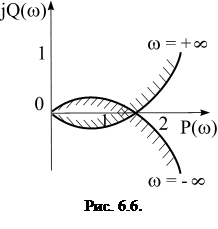
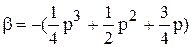
и заменим в нем р на jw

.

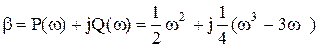Изменяя w от -Ґ до +Ґ, получим кривую, изображённую на рис. 6.6. Значение Q(w) обращается в нуль 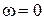при и при 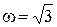, а Р(w) при этих значениям w, будут равны Р(0) = 0 и 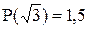. Таким образом определили, что кривая отсекает на оси абсцисс отрезок (0 -1,5), определяющий диапазон изменения b при котором обеспечивается устойчивость системы.

D-разбиение по двум параметрам. Представим характеристическое уравнение системы в виде

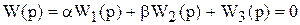, (6.13)

где a и b – свободные параметры системы. Заменим в уравнении р на jw и введем обозначения

(6.14)

Разделив (6.13) на вещественную и мнимую части, получим

.

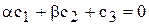
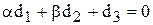Решение этих уравнений даст интересующие нас параметры

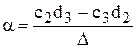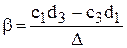, , (6.15)

где .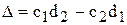

Если D ни при каких значениях w не обращается в нуль, то в плоскости a ,b получаем кривую, являющуюся границей области устойчивости. Если D при каком-либо значении w обращается в нуль, то это может соответствовать двум случаям:

1) при D=0 числители выражений (6.15) не обращаются в нули; в этом случае переход D через нуль может произойти только в бесконечно удалённой точке плоскости a, b;

2) при D=0 числители выражений (6.15) также обращаются в нули; в этом случае получается соотношение

,

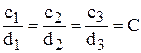т.е. уравнения (6.15) отличаются друг от друга только постоянным множителем С, и одно уравнение является следствием другого. В этом случае для a и b получается бесконечная совокупность точек, лежащих на одной прямой:

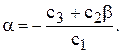
Эта прямая, называется особой, она может пересекать границу области устойчивости или проходить через её начало. Точки особой прямой называются исключительными и в большинстве случаев соответствуют значениям w=0 и w=Ґ. Особая прямая, соответствующая обращению корня в нуль, определяется из условия равенства нулю свободного члена характеристического уравнения, а соответствующая обращению в бесконечность – при приравнивании к нулю коэффициента при старшей степени характеристического уравнения.

Правило штриховки. Для выделения области устойчивости граница D-разбиения штрихуется. Если D>0, то при изменении w от -Ґ до +Ґ штрихуется левая сторона кривой. Если D<0, штрихуется правая сторона. При изменении знака D с плюса на минус штриховка кривой меняется в тех точках, в которых она пересекает особые прямые. Значениям w и -w соответствует одна и та же точка на кривой, поэтому кривая штрихуется дважды с одной и той же стороны, так как D меняет знак при w=0. Особые прямые штрихуются так, чтобы вблизи точек пересечения их с основной кривой штриховка была направлена согласно со штриховкой основной кривой. Если при переходе через точку пересечения знак D изменяется, то направление штриховки особой прямой по обе стороны точки пересечения различны.

6.4. Структурная устойчивость автоматических систем

В ряде случаев оказывается, что система неустойчива при любых значениях параметров, и добиться ее устойчивости можно только изменением структуры. Такие системы называются структурно неустойчивыми. Рассмотрим примеры структурно неустойчивых систем.

Система на рис.6.7 состоит из одного апериодического и двух интегрирующих звеньев. Передаточная функция этой

системы

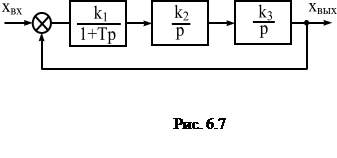
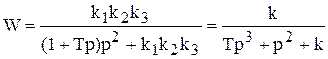
и ее характеристическое уравнение

.

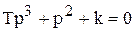Эта система структурно неустойчива, так как один коэффициент характеристического уравнения равен нулю, и поэтому не выполняется необходимое условие устойчивости.

Еще одним примером структурно неустойчивой системы является система, изображенная на рис.6.8. Характеристическое уравнение системы имеет вид

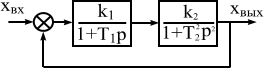
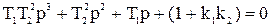
Условием устойчивости по критерию Гурвица является неравенство

Рис.6.8

,

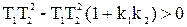что справедливо при условии 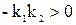. Но так как коэффициенты передачи k₁, k₂ числа положительные, последнее неравенство заведомо невыполнимо.

Задача определения структурной устойчивости в общем виде в настоящее время не решена. Только для некоторых классов одно- и многоконтурных систем сформулированы частные признаки, позволяющие судить о структурной устойчивости. Эти признаки приводятся в литературе в виде таблиц и условий.

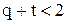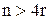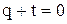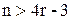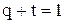Так, в отношении одноконтурных систем существуют следующие условия: система с характеристическим уравнением n-й степени будет структурно устойчива, если при наличии q интегрирующих звеньев, t неустойчивых звеньев или r консервативных звеньев соблюдаются условия: при отсутствии дифференцирующих звеньев и ; при наличии дифференцирующих звеньев и при при должно быть ; при должно быть 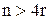; при 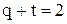должно быть .

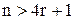Исследования многоконтурных систем с неперекрещивающимися обратными связями показали, что для их структурной устойчивости достаточно (но не необходимо), чтобы этим же свойством обладали все ее участки с внутренними контурами.

Дата добавления: 2014-11-29