Определение начальных условий

Под начальными условиями дина­мического процесса понимается его со­стояние в момент времени, принятый за начало процесса. Начальные усло­вия задаются совокупностью значений выходной координаты исследуемой си­стемы и некоторого числа ее производ­ных при .

Если уравнение динамики представляет собой обыкновенное дифференциальное уравнение n-ного по­рядка, то для его решения необходимо располагать начальными значениями выходной координаты и ее производ­ных по времени до (n-1)-го поряд­ка включительно. Начальные условия называются нулевыми, если начальные значения выходной координаты и ее производ­ных до (n-1)-го порядка включи­тельно все порознь равны нулю. Если хотя бы одно из началь­ных значений не равно нулю, началь­ные условия называются ненулевыми.

При исследовании процессов авто­матического регулирования часто ис­пользуются возмущения, представляю­щие скачкообразное изменение вход­ной координаты или ее производных. Это влечет за собой необходимость до­пущения скачков выходной координа­ты или ее производных в мо­мент приложения подобных возмущений. Начальные значения этих величин будут различными в зависимости от того, будем ли мы приближаться к справа или слева. Например, если ко входу механической системы с одной степенью свободы, находящейся в состоянии равновесия, в некоторый момент вре­мени приложить конечную силу 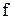то при приближении к началу процесса слева значения как выходной коорди­наты, так и ее производных будут ну­левыми. При приближении к справа уравнение системы для будет таким

(5.1)

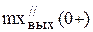где , и 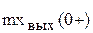предельные значения этих величин для при приближении справа. Так как скорость и перемещение тела, обладающего массой, не могут изменяться скачком, то, следова­тельно, в начальный момент должны соблюдаться условия

, , .

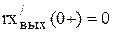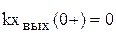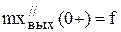В дальнейшем под начальными условиями процесса, описываемого обыкновенным дифференциальным уравнением n-го порядка, будем пони­мать совокупность предельных значе­ний, к которым стремятся величины выходной координаты системы и ее производных до (n - 1)-го порядка включительно при приближении к на­чалу процесса (к t = 0) справа.

При описании сложной системы, имеющей дифференциальное уравнение высокого порядка, реко­мендуется сначала расчленить систему на звенья с одной сте­пенью свободы, а затем для каждого звена от­дельно определять начальные условия. Таким образом, правильное определение начальных условий требует глубокого понимания физического суще­ства задачи и тща­тельного анализа.

5.3. Способы записи математических моделей

Математическая модель физического объекта представляет собой систему соотношений между его внутренними и внешними параметрами. Для автоматических систем такими соотношениями обычно являются дифференциальные и алгебраические уравнения.

Процесс составления математической модели автоматической системы разбивается на два этапа. Cначала составляются математические модели элементов системы, а затем математическая модель всей системы. Дальнейшая работа с моделью определяется тем, какая это модель - линейная или нелинейная.

Нелинейная модель. Если модель нелинейная, то ее упрощения существенно ограничены. Работа с нелинейной моделью, с одной стороны, требует привлечения сложного математического аппарата, а с другой стороны, почти всегда исключает возможность глубоких обобщений. Это затрудняет качественный анализ системы, и поэтому когда это возможно, ее пытаются либо упростить структурно, либо упростить ее математическую формулировку, то есть линеаризовать. Если избавиться от нелинейности не удается, модель решают численными методами.

Линейная модель допускает широкий круг преобразований и может записываться в нескольких формах, основными из которых являются:

1. Модель в виде единого уравнения. Приведение системы уравнений к одному уравнению основано на том, что у соединенных между собой элементов входные переменные одного элемента являются выходными переменными другого, и поэтому исключение промежуточных переменных позволяет такое преобразование проводить.

2. Модель в операторной форме. Операторная форма получается после прямого интегрального преобразования Лапласа исходных уравнений. В зависимости от того, какой режим системы исследуется, эти преобразования могут осуществляться как при нулевых, так и при ненулевых начальных условиях.

3. Модель в виде структурных схем или графов. Структурные схемы или графы модели составляются на основе ее операторных уравнений.

4. Модель в виде передаточных функций. Передаточные функции модели определяются как на основе операторной формы, так и на основе структурных схем или графов.

5.2. Примеры математических моделей элементов

В предыдущей главе приведены примеры составления моделей ряда простейших элементов. Здесь на нескольких примерах покажем технику составления более сложных математических моделей, а также обсудим методы их преобразований.

Математическая модель термопары.В равновесном состоянии, когда температура рабочего спая термопары 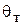равна температуре измеряемой среды 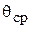, термоэлектродвижущая сила термопары Е определенна и неизменна.

Пусть в какой-то момент времени температура среды скачкообразно возросла на 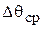. Тогда за счет разности температур измеряемой среды и термопары последняя будет нагреваться до температуры среды, однако процесс нагрева рабочего спая будет проходить не мгновенно, а в течение времени, зависящего от объема и свойств металла спая. Воспользуемся уравнением теплопередачи конвекцией. Количество тепла, переданное от измеряемой среды рабочему спаю термопары за бесконечно малый отрезок времени, равно

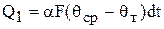, (5.2)

где 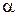– коэффициент теплоотдачи конвекцией; F – поверхность теплопередачи (рабочего спая). Количество тепла, полученное термопарой при нагреве на 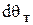градусов, равно

, (5.3)

где m – масса металла рабочего спая; c – удельная теплоемкость металла спая. Так как всегда должно соблюдаться условие 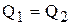, то, приравнивая (5.2) и (5.3) получим

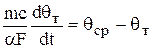. (5.4)

Примем, что зависимость между термо э.д.с. и температурой рабочего спая линейная, то есть

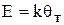, (5.5)

где k – коэффициент пропорциональности. Тогда подстановка 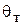из (5.5) в (5.4) даст

.

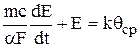Подстановкой получаем стандартное уравнение звена

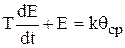(5.6)

Уравнение (5.6) показывает, что при принятых допущениях, термопара является апериодическим звеном первого порядка, входная величина которого - температура измеряемой среды 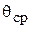, выходная - термоэлектродвижущая сила Е, коэффициент k - коэффициентом передачи звена, а T - постоянной времени звена.

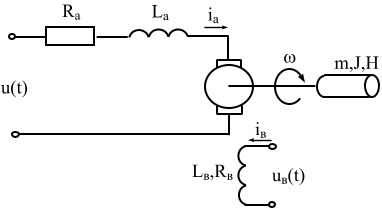
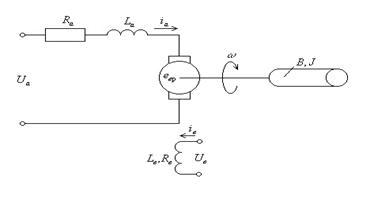
Математическая модель двигателя постоянного тока. Модель двигателя состоит из двух групп уравнений, одна группа описывает внутренние процессы в двигателе, а другая его связи с «внешним окружением». Составим модель ДПТ независимого возбуждения (рис. 5.1).

Уравнения внутренних процессов:

При отсутствии насыщения магнитный поток пропорционален току в обмотке возбуждения

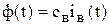. (5.7)

Э.д.с. вращения в якоря пропорциональна частоте вращения 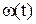и потоку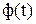

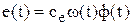. (5.8)

Движущий электромагнитный момент возникает при взаимодействии тока якоря с магнитным потоком

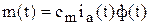. (5.9)

В этих уравнениях постоянные коэффициенты 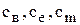учитывают конструктивные параметры машины, и их численные значения легко определяются по паспортным или экспериментальным данным.

Рис. 5.1. Расчетная схема двигателя постоянного тока независимого возбуждения

Уравнения внешних связей. Эти уравнения определены подключением двигателя к внешним объектам: обмотка якоря подключена к источнику напряжения u(t), обмотка возбуждения к источнику напряжения 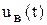и вал двигателя к нагрузке (к рабочему механизму). Уравнения составляются из условий равновесия (или баланса):

уравнение напряжений для обмотки якоря

, (5.10)

уравнение напряжений для обмотки возбуждения

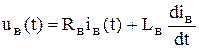, (5.11)

уравнение моментов

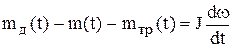, (5.12)

В этих уравнениях 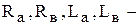активные сопротивления и индуктивности цепей якоря и возбуждения; 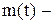момент сопротивления нагрузки; 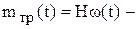момент механических потерь, определяемый коэффициентом трения Н; 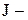момент инерции вращающихся масс. Уравнение моментов составлено на основе второго закона Ньютона, который для вращающихся масс записывается в виде .

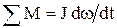Таким образом, математической моделью двигателя постоянного тока независимого возбуждения является система дифференциально-алгебраических уравнений (5.7-5.12). И хотя в модели все элементы линейные (не учитывается насыщение магнитопровода) модель двигателя, тем не менее, нелинейная. Причиной нелинейности являются произведения переменных величин 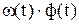и 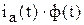в уравнениях (5.8) и (5.9).

Из теории машин постоянного тока известно несколько способов регулирования частоты вращения вала: 1) изменением напряжения якоря (якорное управление); 2) изменением напряжения возбуждения; 3) комбинированное регулирование; 4) изменением сопротивления цепи якоря. Конечно, все эти способы могут быть исследованы на общей модели двигателя полученной выше, но иногда выгоднее отказаться от общей модели и использовать ее более простые версии.

Модель ДПТ при якорном регулировании. Регулирование осуществляется изменением напряжения якоря u(t) при постоянных параметрах цепи возбуждения. Это условие позволяет исключить из модели уравнение для цепи возбуждения (5.11), в результате чего модель становится линейной

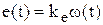
(5.13)

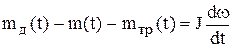
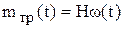
Такую модель можно записать как в операторной форме, так и в виде структурной схемы.

Операторную форму записи модели дает прямое преобразование Лапласа уравнений (5.13). Преобразование при нулевых начальных условиях приводит к следующей системе уравнений

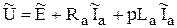
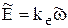
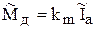(5.14)

.

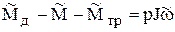
Для представления модели в виде структурной схемы все уравнения в (5.14) должны представлять уравнения звеньев, то есть явно выраженную входную и выходную переменные.

С этой целью первое уравнение в (5.14) перепишем так

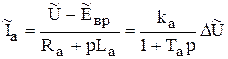(5.15)

где 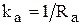- коэффициент передачи и 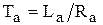- электромагнитная постоянная времени. В таком виде уравнение определяет звено с входным воздействием 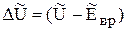и выходным воздействием 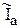. Передаточная функция звена

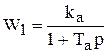. (5.16)

Объединив четвертое и пятое уравнения в (5.14), после преобразований получим

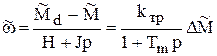, (5.17)

где 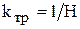- коэффициент передачи и 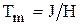- механическая постоянная времени. Передаточная функция этого звена

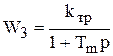. (5.18)

Второе и третье уравнения в (5.14) преобразований не требуют, так как они уже определяют звенья с передаточными функциями

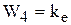, (5.19)

. (5.20)

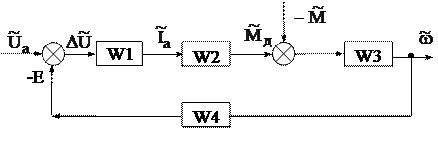
Соединяя звенья между собой, получим модель двигателя в виде структурной схемы (рис. 5.2).

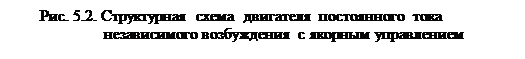Обе формы записи модели, как операторная, так и в виде структурной схемы, позволяют получать все динамические характеристики двигателя, например, , 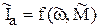и т.д. Покажем процесс получения характеристики с использованием структурной схемы.

Динамика частоты вращения 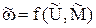. В модели имеются два возмущающих воздействия - напряжение якоря 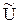и момент нагрузки на валу 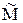. Так как модель линейная, то реакцию двигателя на комбинированное воздействие определим суммированием отдельных реакций.

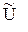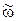Реакция двигателя на изменение напряжения определяется передаточной функцией составленной относительно точек и при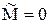

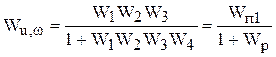, (5.21)

где 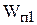- передаточная функция прямого пути прохождения сигнала, 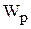- передаточная функция разомкнутой схемы.

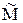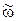Реакция на изменение момента определяется передаточной функцией составленной относительно точек и при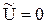

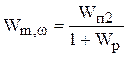, (5.22)

где 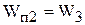- передаточная функция прямого пути прохождения сигнала.

Реакция двигателя на комбинированное действие обоих возмущений будет такой

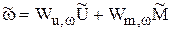. (5.23)

где

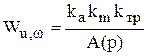, (5.24)

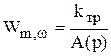. (5.25)

Здесь А(р) - характеристическое уравнение двигателя, которое определяется по формуле

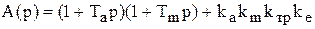(5.26)

или

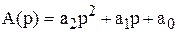, (5.27)

где , , .

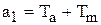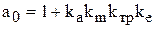Модель ДПТ при регулировании возбуждением. В этом случае регулирование осуществляется изменением напряжения обмотки возбуждения при неизменном напряжении якоря. Это позволяет в исходной модели двигателя переменную 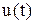заменяется постоянным коэффициентом U и тогда модель запишется следующим образом

,

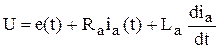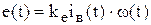
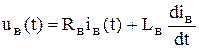, (5.28)

.

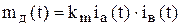
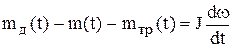Полученная модель двигателя осталась нелинейной, и методы ее решения определяются только характером задач.

Если предполагается исследовать динамику двигателя при глубоких изменениях режимов, таких, например, как, пуск, значительные изменения нагрузки и т.д., то для решения модели надо привлекать специальные математические методы.

Если динамика машины исследуется при малых изменениях в окрестности заданного рабочего режима, то модель можно линеаризовать и использовать ресурсы линейных моделей.

Проведем линеаризацию модели двигателя для режима определенного следующими параметрами 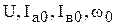. Запишем модель в приращениях переменных

,

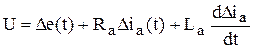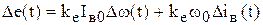
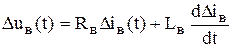, (5.29)

.

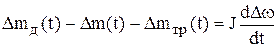Теперь над уравнениями (5.29) проведем преобразование Лапласа, и для упрощения записи опустим символ 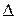и введем обозначения , , ,

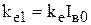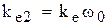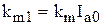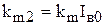
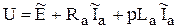
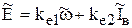
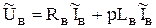(5.30)

.

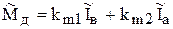
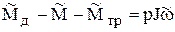Остальные преобразования, такие как построение структурной схемы, получение операторных характеристик двигателя предлагаем читателю провести самостоятельно.

5.3. Пример построения математической модели

автоматической системы

Теперь покажем технику математического моделирования автоматической системы на примере функциональной схемой приведенной на рис. 5.3. Эта система выполняет стабилизацию частоты вращения вала, и в качестве объекта управления в ней использован двигатель постоянного тока независимого возбуждения с якорным управлением. В системе установлены два контура обратных связей.

Контур регулирования скорости является главной ОС системы, он охватывает всю систему с выхода на вход и передает информацию в устройство управления о регулируемом параметре w. Контур содержит датчик скорости (тахогенератор) и регулятор скорости формирующий закон регулирования по скорости.

Контур регулирования тока - является местной ОС и предназначен для ограничения тока якоря. Контур содержит датчик тока (резистор в цепи якоря) и регулятор тока.

Моделирование системы начинается с разработки математических моделей ее элементов. (Уравнения моделей сопровождаются их операторной формой).

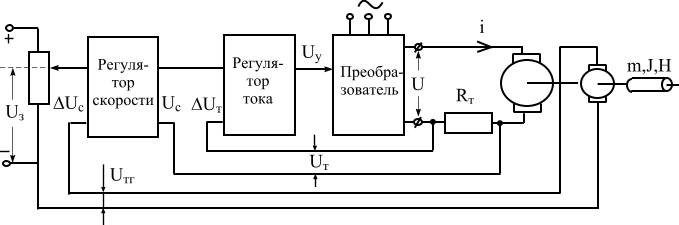
Рис. 5.3. Функциональная схема автоматической стабилизации

частоты вращения вала

Модель регулятора скорости. На вход регулятора скорости поступает сигнал рассогласования по скорости 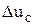, который преобразуется в этом регуляторе по закону

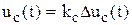, (5.31)

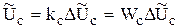. (5.32)

Это так называемый пропорциональный регулятор или П-регулятор.

Модель датчика тока. Датчиком тока служит резистор 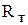, включенный последовательно в якорную цепь двигателя. По закону Ома

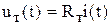(5.33)

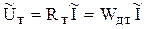. (5.34)

Модель регулятора тока. В регуляторе тока сигнал 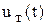преобразуется в сигнал управления 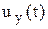в соответствии с выбранным законом регулирования тока. Используем здесь также П-регулятор, тогда

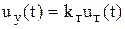, (5.35)

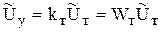. (5.36)

Модель преобразователя. Управление двигателем осуществляется трехфазным преобразователем с линейной зависимостью выходного напряжения u(t) от сигнала управления 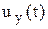. Если пренебречь его инерционностью, то можно записать

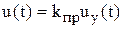, (5.37)

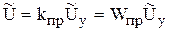. (5.38)

Модель ДПТ. Модель двигателя постоянного тока независимого возбуждения при якорном управлении представлена уравнениями (5.13 и 5.14).

Модель тахогенератора. Обычно тахогенераторы выполняются с линейной статической характеристикой и их инерционностью пренебрегают, поэтому

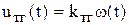, (5.39)

. (5.40)

Математическая модель системы. Для составления модели проследим на функциональной схеме путь прохождения воздействий и их преобразования

1)

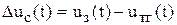
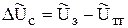
2) ,

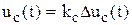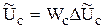
3)

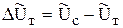
4) ,

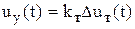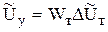
5) , .

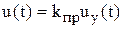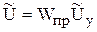6)

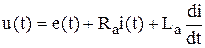
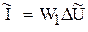
7)

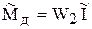
8)

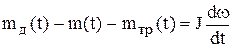
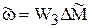
9)

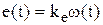
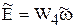
10)

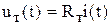
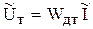
11) .

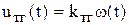
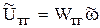Структурная схема соответствующая этим уравнениям представлена на рис. 5.4.

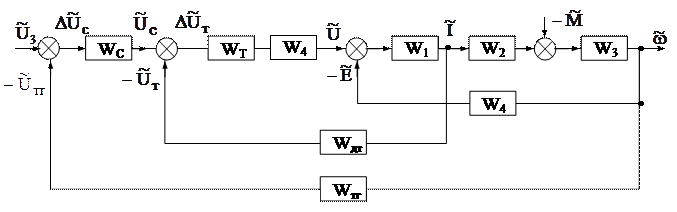
Рис. 5.4.

По этой структурной схеме могут быть построены все динамические характеристики системы. В качестве примера покажем построение одной из них.

Динамика частоты вращения 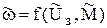. Так как модель содержит два внешних воздействия 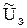и 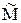, то в силу ее линейности будем определять передаточные функции по каждому воздействию отдельно.

Реакция системы на изменение задания определяется передаточной функцией относительно точек 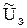, 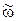при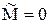

или после подстановок и упрощений

,

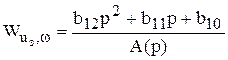где , , .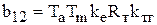

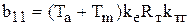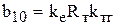Реакция системы на изменение момента нагрузки определяется передаточной функцией относительно точек 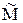, 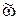при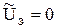

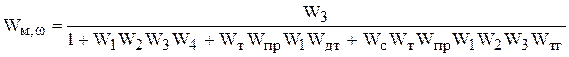
или

,

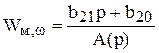где , .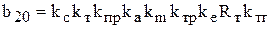

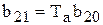В полученных передаточных функциях знаменатель А(р) является характеристическим уравнением системы и определяется уравнением

,

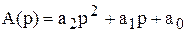где ,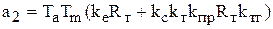

,

.

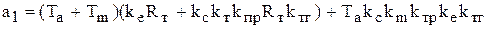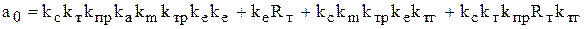По полученным передаточным функциям легко определяется результирующая характеристика системы

.

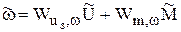Следует заметить, что полученное здесь выражение характеристики представляет собой операторное уравнение, которое требуется с помощью обратного преобразования Лапласа преобразовать в оригинал.

5.4. Методы построения переходных процессов

Для определения числовых значений переходного процесса необ­ходимо иметь его кривую, которую можно получить тремя способа­ми: экспериментально, при помощи моделирования и расчетным путем. Ниже дается обзор некоторых расчетных методов построения переход­ных процессов. Это методы, основанные на решении дифференци­альных уравнений, и частотный метод.

Методы решения диф­ференциального уравнения системы. Эти методы разделяют на точные и приближенные. К точным методам относятся классический и операторный. Различные численные и графические методы решения дифференциаль­ных уравнений являются приближенными.

Классический метод. При решении дифференциального уравнения этим методом возни­кают трудности, связанные с определением корней характеристического уравнения и с решением системы алгебраических уравнений для определения постоянных интегрирования из начальных условий. Эти трудности существенно увеличиваются с возрастанием порядка дифференциального урав­нения. Кроме того, решение дифференциального уравнения значительно услож­няется, когда встречаются не нулевые начальные условия, или правая часть уравнения содержит производные. По этим причинам классический метод в автоматике находит ограниченное применение.

Операторный метод. Решение дифференциального уравнения операторным методом сводится к отысканию оригинала функции по ее известному изображению путем об­ратного преобразования Лапласа. Так, если мы хотим найти переходную функ­цию 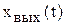, то необходимо знать ее изображение 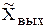и тогда

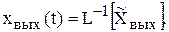
В свою очередь изображение 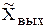легко находится при помощи передаточной функции замкнутой системы по известной формуле

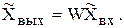
Для отыскания оригинала 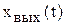существует несколько способов. Можно использовать таблицы изображе­ний, которыми удобно пользоваться при определении переходных функций ти­повых звеньев, так как в таблицах приведены сравнительно простые выражения для изображений. Однако изображение 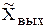для автоматических систем обычно является сложной функцией аргумента р. В этом случае для нахождения оригинала 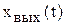лучше подходит теорема разложения.

Операторный метод решения дифференциального уравнения по сравнению с классическим обладает тем преимуществом, что в нем остается только одна трудная операция — определение корней алгебраического уравнения. Вторая трудная операция, связанная с определением по­стоянных интегрирования, отпадает, так как начальные условия учитываются автоматически при составлении передаточной функции системы. Поэтому операторный метод является более удобным, и его часто применяют для решения практических задач автоматического регулирования.

Частотный метод построения переходного процесса. Построение кривой пе­реходного процесса по известным частотным характеристикам системы имеет большое практическое значение, так как не связано с громоздкими вычисления­ми. Кроме того, частотные характеристики можно снять экспериментально.

Этот метод построения переходного процесса основывается на коли­чественной связи между временными и частотными характеристиками, отража­емой преобразованием (интегралом) Фурье

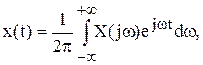
где Х(jw) — изображение Фурье функции х (t) и определяется по формуле

.

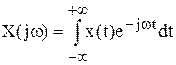Согласно этих формул переходная функция 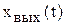(или 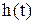для единичного входного воздействия) может быть определена так

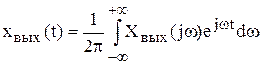. (5.42)

Но так как вести расчеты по этой формуле неудобно, из-за наличия комплексных функций под знаком интеграла, то, учитывая известные соотношения

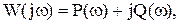
переходный процесс при единичном внешнем воздействии получают по формуле

, (5.43)

либо по формуле

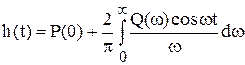, (5.44)

где Р(w) и Q(w) — соответственно вещественная и мнимая частотные характеристики замкнутой системы.

Таким образом, по формуле (5.43) или (5.44) при известной Р(w) или Q(w) можно рассчитать и построить переходную функцию 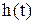. Однако в практических задачах функции Р(w) и Q(w) оказываются сложными и интегралы в формулах (5.43) и (5.44) трудно вычисля­ются. Поэтому возникла задача построения переходной функ­ции h(t) по формуле (5.43) или (5.44) приближенным методом. Эта задача была решена В.В. Солодовниковым, который предложил приближенный графоаналитиче­ский метод построения кривой переходного процесса. Причем для построения переходной функции обычно используют вещественную характеристику Р(w).

Суть метода состоит в следующем. График Р(w) разбивают на типовые трапеции и для каждой трапеции на основании заранее составленных таб­лиц h-функций, рассчитанных при помощи формулы (5.43), строят свой график пере­ходной функции. Искомую переходную функцию находят путем алгебраиче­ского суммирования ординат отдельных составляющих.

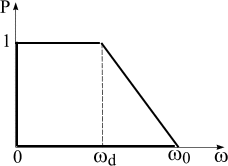
Таблицы h-функций составлены для единичной трапеции, которая характеризуется коэффициентом наклона 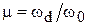(рис. 5.5). Такая таблица позволяет для заданного значения 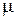построить график переходной характеристики h(t) в функции относительного времени 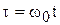, где 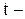текущее время переход­ного процесса. Если высота трапеции не равна единице, то график h(t) соответ­ственно изменит свой масштаб по оси ординат.

Построение переходной функции h(t) производится в следующей последователь­ности:

1. Одним из известных методов определяют зна­чения и строят график вещественной частотной характеристики Р(w) замкну­той системы (рис. 5.6,а}.

2. График Р(w) разбивают на типовые трапеции /, //, ///, для каждой из которых определяют ее параметры 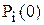, 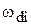и w_0i (рис. 5.5,б).

3. Для каждой из этих трапеций при помощи таблицы h-функций строят график 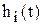, пересчитывая относительное время в натуральное по формуле .

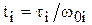4. Искомую переходную функцию находят путем алгебраического сумми­рования ординат переходных функций, соответствующих каждой трапеции.

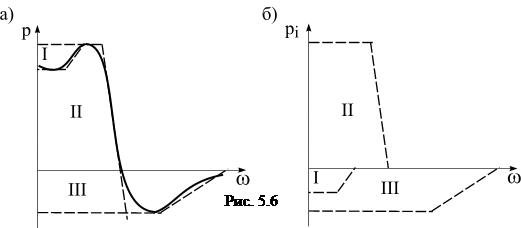
Как показывает практика использования этого метода, его точность вполне достаточна для инженерных расчетов и в значитель­ной степени зависит от точности аппроксимации графика Р(ω) трапециями.

ГЛАВА 6

УСТОЙЧИВОСТЬ АВТОМАТИЧЕСКИХ СИСТЕМ

Дата добавления: 2014-11-29