
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение систем линейных уравнений
|
|
|
|
В общем случае система линейных уравнений имеет вид
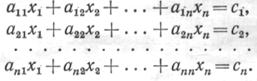
Чтобы эта система имела единственное решение, входящие в нее п уравнений должны быть линейно независимыми. Необходимым и достаточным условием этого является условие неравенства нулю определителя данной системы. Алгоритмы решения задач такого типа подразделяются на прямые и итерационные.
Наиболее распространенные прямые методы основаны на приведении системы уравнений к «треугольному» виду. При этом одно из уравнений содержит только одну неизвестную, а в каждом следующем добавляется еще по одной неизвестной. При счете вручную приведение к треугольному виду достигается сложением и вычитанием уравнений после умножения их на соответствующие постоянные множители. Выполняя эту процедуру вручную, нетрудно ошибиться, однако она позволяет построить удобный алгоритм численного решения на ЭВМ. Одним из используемых для этого методов является метод Гаусса. Применяя его, сначала нормируют первое уравнение, деля его коэффициенты на а11. Затем первое уравнение умножают на первые коэффициенты ai,1 всех других уравнений и последовательно вычитают из остальных уравнений. В результате первая переменная будет исключена из всех уравнений, кроме первого. На следующем этапе решения такая же процедура применяется к остальным п– 1 уравнениям. В результате из оставшихся п– 2 уравнений исключается вторая неизвестная. Всю процедуру повторяют до тех пор, пока после п шагов вся система не будет приведена к треугольному виду. Математически эту процедуру можно описать следующим образом.
На k-м шаге процесса исключения новые нормированные коэффициенты k-ro уравнения имеют вид
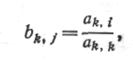
а новые коэффициенты в следующих уравнениях будут иметь вид
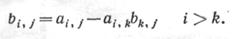
Выполняя эту процедуру, следует помнить, что коэффициенты нижестоящих уравнений ai,j меняются на каждом шаге. Например, коэффициенты bi,j на следующем шаге превращаются в коэффициенты ai,j. Проиллюстрируем применение описанной процедуры на следующем простом примере.
Пусть методом исключения Гаусса требуется решить систему уравнений

Для удобства уравнения обозначим буквами и будем выписывать только коэффициенты при неизвестных и свободные члены уравнений. Тогда исходная система примет вид:

Исключая члены, содержащие x1 получим
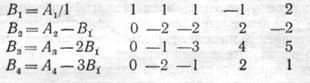
После исключения членов с x2 имеем

Исключение членов с х3 дает
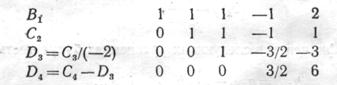
Дойдя до последнего ряда, получим
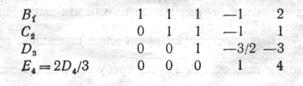
Возвращаясь к форме уравнений, получим
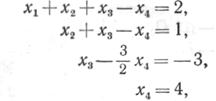
откуда, подставляя значение x4 в 3-е уравнение, х3 — во 2-е и т. д., находим решение системы уравнений
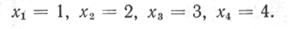
На этом примере хорошо видно, что желательно сделать нулевыми все элементы матрицы коэффициентов, стоящие вне главной диагонали. Последняя процедура называется приведением к диагональному виду и представляет собой усовершенствованную разновидность метода приведения к треугольному виду.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 372; Нарушение авторских прав?; Мы поможем в написании вашей работы!