Метод Ньютона

Метод последовательных приближений, разработанный Ньютоном (другое распространенное название метода — метод касательных), очень широко используется при построении итерационных алгоритмов. Его популярность обусловлена тем, что в отличие от двух предыдущих методов для определения интервала, в котором заключен корень, не требуется находить значения функции с противоположными знаками. Вместо интерполяции по двум значениям функции в методе Ньютона осуществляется экстраполяция с помощью касательной к кривой в данной точке. На рис. 8 показана блок-схема алгоритма этого метода, в основе которого лежит разложение функции f(x) в ряд Тейлора

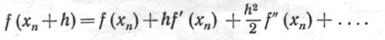
Члены, содержащие h во второй и более высоких степенях, отбрасываются; используется соотношение x_n+h=x_n+1. Предполагается, что переход от х_п к х_п+1 приближает значение функции к нулю так, что f(x_n+h)=0. Тогда

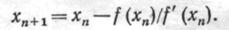
Значение x_n+1 соответствует точке, в которой касательная к кривой в точке х_п пересекает ось х. Так как кривая f(x) отлична от прямой, то значение функции f(x_n+1) скорее всего не будет в точности равно нулю. Поэтому вся процедура повторяется, причем вместо х_n используется х_n+1. Счет прекращается по достижении достаточно малого значения f(x_n+1). На рис. 9 процесс решения уравнения методом Ньютона показан графически. Совершенно ясно, что быстрота сходимости в большой мере зависит от удачного выбора исходной точки. Если в процессе итераций тангенс угла наклона касательной f’(x) обращается в нуль, то применение метода осложняется. Можно также показать, что в случае бесконечно большого f”(x) метод также не будет достаточно эффективным. Так как условие кратности корней имеет вид f(x) = f’(x) = 0, то в этом случае метод Ньютона не обеспечивает сходимость. Отметим, что иногда используется другой способ контроля сходимости, состоящий в сравнении х_п и x_n+1.

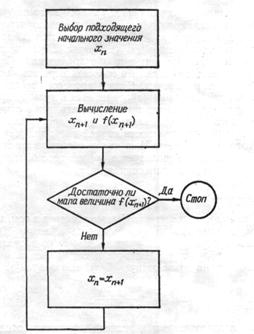
Рис. 8. Блок-схема алгоритма метода Ньютона.

Рис. 9. Метод Ньютона.

Дата добавления: 2014-11-29