Решение обыкновенных дифференциальных уравнений

Дифференциальными называются уравнения, содержащие одну или несколько производных. Инженеру очень часто приходится сталкиваться с ними при разработке новых изделий или технологических процессов, так как большая часть законов физики формулируется именно в виде дифференциальных уравнений. В сущности, любая задача проектирования, связанная с расчетом потоков энергии или движения тел, в конечном счете, сводится к решению дифференциальных уравнений. К сожалению, лишь очень немногие из них удается решить без помощи вычислительных машин. Поэтому численные методы решения дифференциальных уравнений играют такую важную роль в практике инженерных расчетов.

В зависимости от числа независимых переменных и, следовательно, типа входящих в них производных дифференциальные уравнения делятся на две существенно различные категории: обыкновенные, содержащие одну независимую переменную и производные по ней, и уравнения в частных производных, содержащие несколько независимых переменных и производные по ним, которые называются частными. Рассмотрим методы решения обыкновенных дифференциальных уравнений.

Чтобы решить обыкновенное дифференциальное уравнение, необходимо знать значения зависимой переменной и (или) ее производных при некоторых значениях независимой переменной. Если эти дополнительные условия задаются при одном значении независимой переменной, то такая задача называется задачей с начальными условиями, или задачей Коши. Если же условия задаются при двух или более значениях независимой переменной, то задача называется краевой. В задаче Коши дополнительные условия называют начальными, а в краевой задаче — граничными. Часто в задаче Коши в роли независимой переменной выступает время. Примером может служить задача о свободных колебаниях тела, подвешенного на пружине. Движение такого тела описывается дифференциальным уравнением, в котором независимой переменной является время t. Если дополнительные условия заданы в виде значений перемещения и скорости при t=0, то имеем задачу Коши. Для той же механической системы можно сформулировать и краевую задачу. В этом случае одно из условий должно состоять в задании перемещения по истечении некоторого промежутка времени. В краевых задачах в качестве независимой переменной часто выступает длина. Известным примером такого рода является дифференциальное уравнение, описывающее деформацию упругого стержня. В этом случае граничные условия обычно задаются на обоих концах стержня.

Задача Коши

Задачу Коши можно сформулировать следующим образом. Пусть дано дифференциальное уравнение

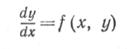
и начальное условие у(х₀)=у₀. Требуется найти функцию у(х), удовлетворяющую как указанному уравнению, так и начальному условию. Обычно численное решение этой задачи получают, вычисляя сначала значение производной, а затем задавая малое приращение х и переходя к новой точке x₁=x₀+h. Положение новой точки определяется по наклону кривой, вычисленному с помощью дифференциального уравнения. Таким образом, график численного решения представляет собой последовательность коротких прямолинейных отрезков, которыми аппроксимируется истинная кривая y=f(x). Сам численный метод определяет порядок действий при переходе от данной точки кривой к следующей.

Поскольку численное решение задачи Коши широко применяется в различных областях науки и техники, то оно в течение многих лет было объектом пристального внимания и число разработанных для него методов очень велико.

Рассмотрим одношаговые методы, в которых для нахождения следующей точки на кривой y=f(x) требуется информация лишь об одном предыдущем шаге. Одношаговыми являются метод Эйлера и методы Рунге— Кутта.

Одношаговые методы предназначены для решения дифференциальных уравнений первого порядка вида

где y'=dy/dx, при начальном условии у(х₀)=x₀. С помощью этих методов вычисляют последовательные значения у, соответствующие дискретным значениям независимой переменной х.

Дата добавления: 2014-11-29