Методы Рунге

Чтобы удержать в ряде Тейлора член n-го порядка, необходимо каким-то образом вычислить n -ю производную зависимой переменной. При использовании модифицированного метода Эйлера для получения второй производной в конечно-разностной форме достаточно было знать наклоны кривой на концах рассматриваемого интервала. Чтобы вычислить третью производную в конечно-разностном виде, необходимо иметь значения второй производной по меньшей мере в двух точках. Для этого необходимо дополнительно определить наклон кривой в некоторой промежуточной точке интервала h, т. е. между х_n и x_n₊₁. Очевидно, чем выше порядок вычисляемой производной, тем больше дополнительных вычислений потребуется внутри интервала. Метод Рунге — Кутта дает набор формул для расчета координат внутренних точек, требуемых для реализации этой идеи. Так как существует несколько способов расположения внутренних точек и выбора относительных весов для найденных производных, то метод Рунге — Кутта в сущности объединяет целое семейство методов решения дифференциальных уравнений первого порядка. Наиболее распространенным из них является метод, при котором удерживаются все члены, включая h ⁴. Это метод четвертого порядка точности, для которого ошибка на шаге имеет порядок h ⁵. Расчеты при использовании этого классического метода производятся по формуле

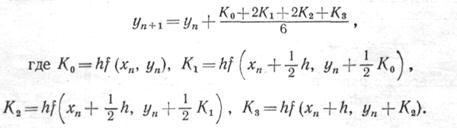
Метод Эйлера и его модификация по сути дела являются методами Рунге — Кутта первого и второго порядка соответственно. По сравнению с ними метод Рунге — Кутта имеет важное преимущество, так как обеспечивает более высокую точность, которая с лихвой оправдывает дополнительное увеличение объема вычислений. Более высокая точность метода Рунге— Кутта часто позволяет увеличить шаг интегрирования h. Допустимая погрешность на шаге определяет его максимальную величину. Чтобы обеспечить высокую эффективность вычислительного процесса, величину h следует выбирать именно из соображений максимальной допустимой ошибки на шаге. Такой выбор часто осуществляется автоматически и включается как составная часть в алгоритм, построенный по методу Рунге — Кутта.

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. - М.: Лаборатория Базовых Знаний, 2001 г. - 632с.

2. Вержбицкий В.М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения): Учебное пособие для вузов. -. М.: Высшая школа, 2001 г. - 382 с.

3. Демидович Б.П., Марон И.А. Основы вычислительной математики. М.,1966г.- 664 с.

4. Марчук Г.И. Методы вычислительной математики. М.: Наука. Главная редакция физико-математической литературы, 1980г. – 535 с.

5. Турчак Л.И. Основы численных методов. – М.: Наука, 1987 г.

6. Самарский А.А., Гулин А.В. Численные методы. – М.: Наука. 1989 г.

7. Березин И.С., Жидков Н.П. Методы вычислений. М.: Наука, т.I, 1966 - 632 с.

8. Калиткин Н.Н. Численные методы. М.: Наука, 1978 г., 512 с.

9. Мысовских И.П. Лекции по методам вычислений. М.: Наука, 1982 г. - 342 с.

по дисциплине “Физико-математические основы техники высоких напряжений” для студентов КФ ПетрГУ специальности «Электроэнергетика и электроника» физико-энергетического факультета

Общие указания по выполнению и оформлению контрольной работы:

1. В заданиях контрольной работы не требуется составления программ на компьютере. Все промежуточные вычисления, а также расчетные формулы, применяемые в этих заданиях, должны быть представлены в контрольной работе.

2. Контрольная оформляется в рукописном виде, без использования компьютерного набора (за исключением титульного листа). Работы, распечатанные на принтере или копировальном аппарате НЕ ПРИНИМАЮТСЯ!

3. Оформленная контрольная работа должна содержать: титульный лист с указанием фамилии, имени, отчества студента, текст задания; графический и словесный алгоритм решения задачи. Графики строятся на миллиметровой бумаге.

4. Вариант задания выбирается по номеру в списке группы.

Задание 1. Решить методом Гаусса систему линейных алгебраических уравнений

Проверить полученное решение подстановкой в систему уравнений.

Вариант
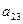
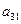
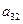
			-7				-2	-1				-9
			-7	-1				-1
	-3			-1				-1				-13
	-3			-1	-4			-1		-8	-19
	-3		-1		-3		-5				-15	-9
	-3			-1	-3					-28	-1	-15
			-1		-3		-5
			-1		-2				-1		-1
			-1		-2		-4		-1		-14
		-2	-1				-4			-4
		-2	-1			-3	-4		-2			-18
		-2	-1			-3			-2		-9	-16
			-1							-13		-8
			-1			-3	-3					-2
			-1	-2			-3				-17
			-1	-2			-3			-12		-2
			-1	-2	-1					-9		-1
			-1	-2	-1						-4
			-1	-2	-1				-6		-4
			-1	-2	-1				-2		-3
							-2
			-1		-2		-2	-2	-1			-9
			-1				-2		-1
			-2				-2		-3	-16
			-2				-2		-3	-11	-8
			-2				-2		-3
			-2				-2		-3
			-2				-2		-3

											-3
		-6			-3			-5
	-3							-1		-14
		-3			-2			-3		-4	-1	-3
			-1	-8			-5				-8	-15
					-2					-2		-10
					-2						-15	-6
			-1		-6		-4		-1		-42
			-1				-4				-8	-13
			-2			-3	-2		-1			-9
			-1			-3			-4		-9
										-8		-8
						-3			-4
			-1				-3					-13
				-2			-3			-12	-14	-2
	-1			-2	-1					-5		-1
						-2
				-2	-1				-6		-4
				-2	-1						-3
					-1	-3	-2
					-2			-1

Задание 2. Вычислить указанным методом на отрезке

корень уравнения

с точностью до четырех верных знаков. Проверить полученное решение подстановкой в уравнение.

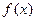
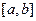
Вариант			Метод
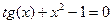
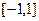
			половинного деления
			половинного деления
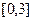
			половинного деления
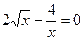
			половинного деления
			половинного деления
			половинного деления
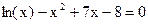
			половинного деления
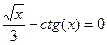
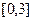
			половинного деления
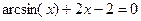
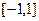
			половинного деления
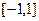
			половинного деления
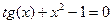
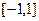
			ложного положения
			ложного положения
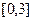
			ложного положения
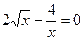
			ложного положения
			ложного положения
			ложного положения
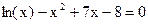
			ложного положения
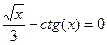
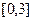
			ложного положения
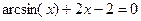
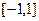
			ложного положения
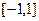
			ложного положения
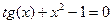
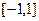
			секущих
			секущих
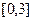
			секущих
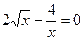
			секущих
			секущих
			секущих
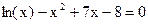
			секущих
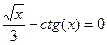
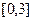
			секущих
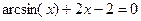
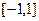
			секущих
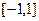
			секущих
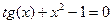
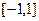
			Ньютона
			Ньютона
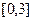
			Ньютона
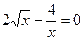
			Ньютона
			Ньютона
			Ньютона
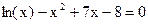
			Ньютона
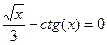
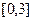
			Ньютона
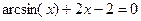
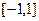
			Ньютона
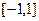
			Ньютона
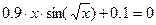
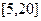
			половинного деления
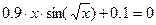
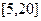
			ложного положения
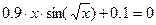
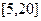
			секущих
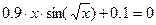
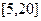
			Ньютона
			половинного деления
			ложного положения
			секущих
			Ньютона
			простой итерации
			простой итерации

Задание 3. Вычислить указанным методом определенный интеграл

от функции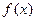

, заданной на отрезке

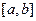с шагом

. Сравнить с точным значением, оценить погрешность.

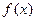
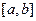
Вариант		Метод
	0.4	прямоугольников
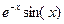
	0.4	прямоугольников
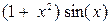
	0.4	прямоугольников
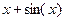
	0.4	прямоугольников
	0.4	прямоугольников
	0.4	прямоугольников
	0.4	прямоугольников
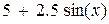
	0.4	прямоугольников
	0.4	прямоугольников
	0.4	прямоугольников
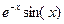
	0.4	трапеций
	0.4	трапеций
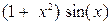
	0.4	трапеций
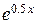
	0.4	трапеций
	0.4	трапеций
	0.4	трапеций
	0.4	трапеций
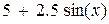
	0.4	трапеций
	0.4	трапеций
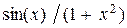
	0.4	трапеций
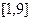
	0.4	трапеций
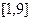
	0.4	прямоугольников
	0.1	прямоугольников
	0.1	прямоугольников
	0.1	прямоугольников
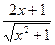
	0.1	прямоугольников
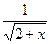
	0.1	прямоугольников
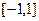
	0.1	прямоугольников
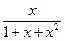
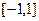
	0.1	прямоугольников
	0.1	трапеций
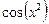
	0.1	трапеций
	0.1	трапеций
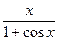
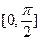
	0.1	трапеций
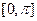
	0.1	трапеций
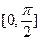
	0.1	трапеций
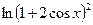
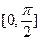
	0.1	трапеций
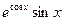
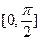
	0.1	прямоугольников
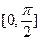
	0.1	прямоугольников
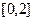
	0.1	прямоугольников
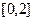
	0.1	прямоугольников
	0.1	прямоугольников
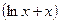
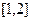
	0.1	прямоугольников
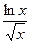
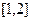
	0.1	прямоугольников
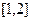
	0.1	трапеций
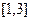
	0.1	трапеций
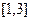
	0.1	трапеций
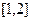
	0.1	трапеций
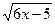
	0.1	трапеций
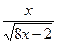
	0.1	трапеций

«Физико-математические основы техники высоких напряжений»

1.	Абсолютная и относительная погрешности приближенного числа.
2.	Аппроксимация и интерполирование функций. Интерполирование сплайнами.
3.	Аппроксимация и интерполирование функций. Интерполяционная формула Ньютона.
4.	Аппроксимация и интерполирование функций. Метод наименьших квадратов.
5.	Вычисление первых производных по трёхточечным схемам.
6.	Задача Коши для обыкновенного дифференциального уравнения.
7.	Интерполяционный многочлен Лагранжа.
8.	Квадратурные формулы Ньютона – Котеса.
9.	Краевая задача для обыкновенного дифференциального уравнения.
10.	Метод конечных разностей решения обыкновенных дифференциальных уравнений.
11.	Метод ложного положения.
12.	Метод Ньютона решения системы нелинейных уравнений.
13.	Метод половинного деления.
14.	Метод последовательных приближений решения нелинейных уравнений.
15.	Метод простой итерации.
16.	Метод секущих.
17.	Многошаговые методы Адамса-Башфорта.
18.	Модифицированный метод Эйлера.
19.	Неявные методы Адамса-Ноултона.
20.	Область притяжения корня для итерационных методов решения уравнений.
21.	Погрешности квадратурных формул при вычислении определенных интегралов.
22.	Погрешности основных арифметических операций.
23.	Погрешность интерполяционного полинома.
24.	Погрешность результата численного решения задачи.
25.	Понятия значащей, верной и сомнительной цифры в записи приближенного числа.
26.	Порядок погрешности аппроксимации производной.
27.	Правила округления и погрешность округления.
28.	Представление чисел в ЭВМ. Погрешности арифметических операций в ЭВМ.
29.	Приближенные вычисления определенных интегралов. Квадратурная формула Гаусса.
30.	Приближенные вычисления определенных интегралов. Метод Монте-Карло.
31.	Приближенные вычисления определенных интегралов. Формула прямоугольников.
32.	Приближенные вычисления определенных интегралов. Формула трапеций.
33.	Причины возникновения и классификация погрешности.
34.	Решение обыкновенных дифференциальных уравнений. Метод Эйлера.
35.	Решение обыкновенных дифференциальных уравнений. Методы Рунге — Кутта.
36.	Решение систем линейных уравнений.
37.	Решение систем линейных уравнений. Метод Гаусса.
38.	Решение систем линейных уравнений. Методом Зейделя.
39.	Решение систем линейных уравнений. Методом простой итерации
40.	Формула Симпсона (формула парабол).
41.	Численное дифференцирование. Вычисление производных второго порядка.
42.	Численное дифференцирование. Первая производная. Двухточечные методы.
43.	Численное решение алгебраических и трансцендентных уравнений. Метод Ньютона.
44.	Численное решение уравнений. Локализация (отделение) корней.
45.	Численные методы для решения систем нелинейных уравнений.

Методы Рунге — Кутта