Модифицированный метод Эйлера

Хотя тангенс угла наклона касательной к истинной кривой в исходной точке известен и равен у'(х₀) он изменяется в соответствии с изменением независимой переменной. Поэтому в точке x₀+h наклон касательной уже не таков, каким он был в точке х_л. Следовательно, при сохранении начального наклона касательной на всем интервале h в результаты вычислений вносится погрешность. Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию производной. Это можно сделать, например, используя среднее значение производной в начале и конце интервала. В модифицированном методе Эйлера сначала вычисляется значение функции в следующей точке по методу Эйлера:

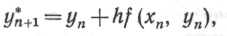
которое используется для вычисления приближенного значения производной в конце интервала f(x_n+1, у*_п+1). Вычислив среднее между этим значением производной и ее значением в начале интервала, найдем более точное значение у_п+1:

.

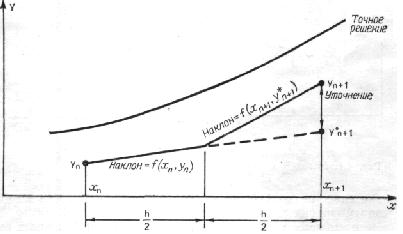
Рис. 15. Модифицированный метод Эйлера.

Этот прием иллюстрируется на рис. 15. Принцип, на котором основан модифицированный метод Эйлера, можно пояснить и иначе. Для этого вернемся к разложению функции в ряд Тейлора

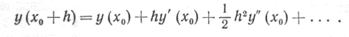
Кажется очевидным, что, сохранив член с h ² и отбросив члены более высоких порядков, можно повысить точность. Однако чтобы сохранить член с h ², надо знать вторую производную у"(х₀). Ее можно аппроксимировать конечной разностью:

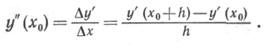
Подставив это выражение в ряд Тейлора с отброшенными членами второго порядка, найдем

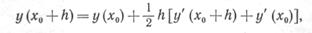
что совпадает с ранее полученным выражением.

Этот метод является методом второго порядка, так как в нем используется член ряда Тейлора, содержащий h ². Ошибка на каждом шаге при использовании этого метода, имеет порядок h³. За повышение точности приходится расплачиваться дополнительными затратами машинного времени, необходимыми для вычисления у*_п+1. Более высокая точность может быть достигнута, если пользователь готов потратить дополнительное машинное время на лучшую аппроксимацию производной путем сохранения большего числа членов ряда Тейлора. Эта же идея лежит в основе методов Рунге — Кутта.

Дата добавления: 2014-11-29