Игольчатая вариация и условие оптимальности

Предположим, что задача оптимального управления решена и найдено оптимальное управление (рис. 20,а) и соответствующая ему оптимальная траектория (рис. 20,б).

Заменим оптимальное управление на другое управление, которое отличается от оптимального на бесконечно малом интервале времени . Такая вариация управляющего воздействия называется игольчатой вариацией. Игольчатая вариация не должна выходить за пределы ограничения, наложенного на управляющее воздействие.

Под влиянием игольчатой вариации ОУ после момента времени будет двигаться по траектории , отличной от траектории , и придет в другое конечное состояние . Так как конечное состояние ОУ не задавалось, то изменение конечного состояния по сравнению с оптимальным является допустимым, что упрощает доказательство принципа максимума. Именно поэтому рассматривается задача со свободным правым концом траектории. Задача с закрепленным правым концом доказывается значительно сложнее.

Отклонение между траекториями и охарактеризуем вектором . Найдем его для момента времени : .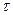

Векторы 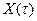и разложим в ряд Тейлора в окрестности момента времени и ограничим разложение двумя членами:

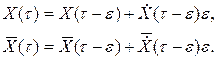
Так как векторы и совпадают, то вектор отклонения

.

Участки траекторий и между моментами времени и 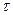будем считать линейными; для линейных участков производные имеют одно и то же значение в любой точке участка. Поэтому производные в момент времени заменим производными в момент времени : .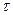

Производную от вектора состояния заменим правой частью уравнения ОУ . Получим

. (17)

Соотношение (17) можем считать первым результатом доказательства.

Рассмотрим первый элемент вектора , т.е. величину в момент времени t=T: . Здесь - показатель качества, который соответствует оптимальному управлению и достигает минимального значения, - показатель качества, который соответствует управлению, содержащему игольчатую вариацию, и следовательно, отличается от оптимального в большую сторону. Поэтому величина или .

Данное неравенство содержит лишь первый элемент вектора . Введем в неравенство весь вектор . Сделаем это с помощью дополнительного вектора :

.

Это неравенство соответствует моменту времени ; распространим его на весь интервал управления . Будем считать, что существует такой вектор P(t), который удовлетворяет условию:

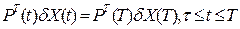. (18)

Условие (18) выполняется для всех моментов времени в интервале , в том числе и для момента времени 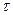. Поэтому исходное неравенство представим в виде:

.

Подставим в это неравенство вектор из соотношения (17):

.

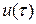Положительный сомножитель , независящий от , опустим из рассмотрения и преобразуем неравенство:

.

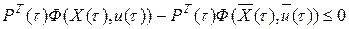В левой части неравенства доминирует второе слагаемое. Оно определяется оптимальным управлением и не зависит от игольчатой вариации. Если уменьшать игольчатую вариацию, то разница между первым и вторым слагаемыми должна уменьшаться за счет увеличения первого из них. В тот момент, когда высота игольчатой вариации совпадет с оптимальным управлением, первое слагаемое достигнет максимума, а неравенство превратится в равенство. Отсюда вытекает условие оптимальности принципа максимума:

.

Так как момент времени 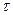выбран произвольным образом внутри интервала , заменим его текущим временем t:

.

Левую часть этого соотношения называют функцией Гамильтона или гамильтонианом и обозначают через . На практике используется скалярная форма условия оптимальности:

.

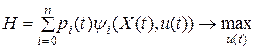Оптимальное управление, найденное из условия оптимальности, будет содержать неизвестные функции , входящие в состав вектора . Вектор введен в рассмотрение с помощью соотношения (18), которое и лежит в основе его нахождения.

Продифференцируем левую и правую части соотношения (18) по времени , учитывая, что в левой части стоит произведение векторов, а правая часть не зависит от :

. (19)

Рассмотрим вектор 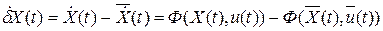. Заметим, что на интервале управления и совпадают (рис. 20), а вектор . Поэтому . Второе слагаемое разложим в ряд Тейлора, ограниченный линейными членами:

.

В итоге вектор примет вид

.

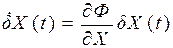Подставим этот вектор в уравнение (19), вынесем вектор за скобки вправо:

.

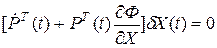Вектор 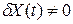, так как обусловлен последствиями игольчатой вариации, поэтому тождественное равенство нулю может быть достигнуто только за счет условия

или ,

если левое выражение подвергнуть операции транспонирования. Таким образом, получено дифференциальное уравнение в векторно-матричной форме для нахождения вектора , содержащего неизвестные функции . Это уравнение в скалярной форме имеет вид:

. (20)

Здесь - элементы квадратной матрицы размером .

Дата добавления: 2014-11-29