Обобщения принципа максимума

В разделе 3.2 рассмотрено доказательство принципа максимума Понтрягина для задачи с фиксированным временем управления и свободным правым концом траектории. Решение задачи состоит из следующих этапов:

- на основании показателя качества вводится дополнительная переменная , обладающая свойствами:

;

- записывается условие оптимальности , где функция определена на предыдущем этапе, функции , берутся из исходных уравнений ОУ, функции , являются вспомогательными неизвестными функциями. Из условия оптимальности находится структура оптимального управления;

- для нахождения функций , формируется система дифференциальных уравнений (20). В некоторых задачах эта система уравнений содержит еще и переменные состояния 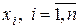, и поэтому может быть решена только совместно с исходными уравнениями ОУ. Возникающие здесь постоянные интегрирования находятся на основании векторов 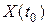и . В других задачах, как например, в задаче о рекламной деятельности, система уравнений (20) содержит только неизвестные функции 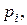и может быть решена изолированно. Возникающие здесь постоянные интегрирования вычисляются на основании вектора .

Эта схема в целом переносится на задачи оптимального управления с другими конечными условиями. Рассмотрим возникающие здесь особенности.

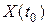Задача с фиксированным временем и закрепленным правым концом. Решение задачи состоит из тех же этапов, но теперь вектор , причем величины , являются неизвестными и не могут участвовать в нахождении постоянных интегрирования. Постоянные интегрирования вычисляются с помощью векторов и .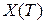

Если система дифференциальных уравнений (20) не содержит переменных состояния и может быть решена изолированно, то возникает проблема нахождения постоянных интегрирования, так как не известны ни начальное , ни конечное значения вектора . Эта проблема решается путем подбора такого начального или конечного значения вектора , при котором оптимальная траектория ОУ пройдет через заданное конечное состояние .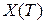

Более подробно процедура подбора выглядит так. Задаются произвольным вектором , решают систему уравнений (20) и находят вспомогательные функции , подставляют их в выражение для оптимального управления, для найденного управления решают уравнения ОУ и находят его траекторию, сравнивают конечное состояние ОУ с заданным. Изменяют вектор таким образом, чтобы после многократных вычислений траектория ОУ прошла через заданную конечную точку .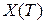

Если система уравнений (20) допускает аналитическое решение, как в задаче о рекламной деятельности, то целесообразнее подбирать не вектор , а постоянные интегрирования.

Задача с нефиксированным временем и свободным правым концом. В данном варианте задачи вектор , а для функции Гамильтона справедливо условие: 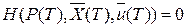. Это условие служит поводом для отыскания незаданного момента времени 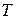. С учетом структуры вектора это условие принимает вид: .

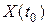Задача с нефиксированным временем и закрепленным правым концом. В данном варианте задачи вектор , причем величины , являются неизвестными и не могут участвовать в нахождении постоянных интегрирования. Постоянные интегрирования вычисляются с помощью векторов и 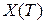. Для функции Гамильтона справедливо условие: 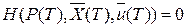. Это условие служит поводом для отыскания незаданного момента времени .

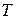Задача оптимального управления в форме Больца. В этой задаче критерий оптимальности содержит интегральную и терминальную составляющие:

.

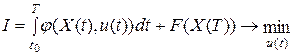Решение задачи имеет следующие особенности. Дополнительная переменная , функция Гамильтона и система уравнений (20) формируются только на основе интегральной составляющей. На последнем этапе при нахождении постоянных интегрирования подключается терминальная составляющая в виде условий трансверсальности

.

3.5. Пример: задача о рекламной деятельности в форме Больца

Вернемся к задаче о рекламной деятельности фирмы и предположим, что на первом этапе рекламная политика фирмы проводилась на основании результатов примера 3.3. В качестве показателя качества использовался функционал

,

который представляет собой суммарный объем продаж за вычетом расходов на рекламу. Требовалось максимизировать этот функционал.

На втором этапе планирования рекламной деятельности руководство фирмы решило изменить подход к формированию критерия оптимальности и желает добиться максимального объема продаж в конечный момент времени 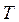при минимальных суммарных затратах на рекламу. Такому требованию отвечает критерий

.

С помощью коэффициентов руководство фирмы может расставить свои приоритеты затратам на рекламу и конечному объему продаж. В такой постановке данная задача представляет собой задачу Больца.

Уравнение, связывающее объем продаж 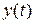с затратами на рекламу , имеет тот же вид:

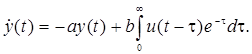
Затраты на рекламу по-прежнему подвержены ограничению .

В разделе 1.2 исходное уравнение было преобразовано в дифференциальное уравнение второго порядка

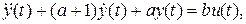(25)

а затем с помощью переменных состояния 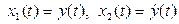представлено в виде системы двух дифференциальных уравнений первого порядка, записанных в нормальной форме Коши:

Для решения задачи потребуются начальные условия, в качестве которых будут использованы конечные результаты из предыдущего этапа, т.е. из примера 3.3: и .

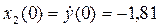Запишем критерий оптимальности с учетом переменных состояния:

.

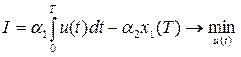Если сопоставить этот критерий оптимальности с общей задачей Больца, то терминальная составляющая здесь имеет вид: .

Начальный этап решения задачи проводится только на основании интегральной составляющей. Введем в рассмотрение дополнительную переменную состояния x ₀(t):

.

Составим функцию Гамильтона и запишем условие оптимальности принципа максимума:

.

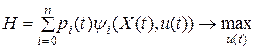В условиях данного примера

.

Функция Гамильтона и условие оптимальности примут вид:

Преобразуем гамильтониан, оставив в нем только те слагаемые, которые зависят от u (t), и представим условие оптимальности в более компактной форме:

С учетом ограничения 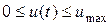получим следующую структуру оптимальных затрат на рекламу:

Таким образом, оптимальные затраты на рекламу лежат на границах ограничения и в определенные моменты времени переходят с одной границы на другую. Моменты переходов определяются функцией переключения

.

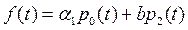Она содержит неизвестные функции p ₀(t) и p ₂(t), которые могут быть найдены из системы уравнений

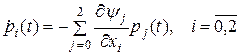. (26)

Рассмотрим первое уравнение из этой системы для :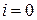

.

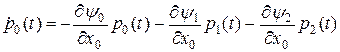Так как функции 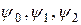не зависят от 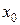, то все частные производные здесь равны нулю и уравнение примет вид 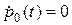. Следовательно 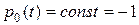, так как .

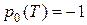Рассмотрим второе уравнение из системы (26) для :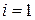

.

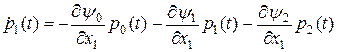Здесь частные производные , и с учетом 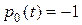второе уравнение примет вид: .

Рассмотрим третье уравнение из системы (26) для :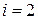

.

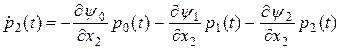Здесь частные производные 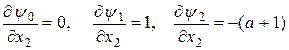, и третье уравнение примет вид .

Таким образом, для нахождения функци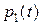й и 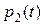нужно решить систему дифференциальных уравнений

при конечных условиях, вытекающих из условий трансверсальности. Если из первого уравнения выразить неизвестную функцию 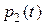и подставить ее во второе уравнение, то придем к одному дифференциальному уравнению второго порядка относительно неизвестной функции :

.

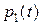Это линейное однородное дифференциальное уравнение с постоянными коэффициентами. Его решение находится на основании характеристического уравнения 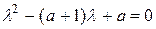с корнями 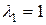, 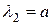. Общее решение дифференциального уравнения имеет вид

.

Для отыскания постоянных интегрирования 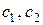применим условия трансверсальности

.

Отсюда следует, что

Сначала найдем функцию

,

а затем составим систему уравнений

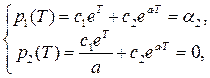
Из решения этой системы получим постоянные интегрирования:

, .

В итоге найдём функцию

и сформируем функцию переключения

.

Обратимся к числовому примеру. Пусть а =0,2; b =1; u_max =5; Т =7; 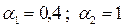. В этих условиях функция переключения примет вид:

.

Результаты решения задачи представлены на рис. 22. На верхнем графике изображена функция переключения f (t), которая два раза меняет свой знак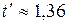: при и при . Поэтому оптимальное управление (затраты на рекламу) состоит из трех участков. На начальном этапе планируемого периода 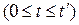средства на рекламу не выделяются; на втором этапе на рекламу должны тратиться все выделяемые средства; на третьем этапе 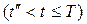средства на рекламу не выделяются. Последний график отражает изменение объема продаж у (t) рекламируемого товара.

Рис. 22

Изменим параметр при сохранении остальных параметров. Пусть 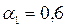. Новый вариант отличается от предыдущего более высокой приоритетностью затрат на рекламу, поэтому следует ожидать их уменьшения. В новых условиях функция переключения примет вид:

.

Соответствующие результаты представлены на рис. 23. Функция переключения f (t) по-прежнему два раза меняет свой знак: при и при , однако протяженность второго участка, на котором реклама проводится по полной программе, сократилась. Естественно, уменьшился объем продаж рекламируемого товара в конечный момент времени .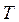

Рис. 23

Объём продаж 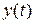, приведенный на этих графиках, найден путем решения дифференциального уравнения:

,

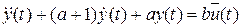причем решение состоит из трех участков.

На первом участке 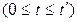оптимальное управление 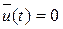, и исходное уравнение примет вид

.

Начальные условия . Процесс решения аналогичен решению дифференциального уравнения для 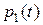, поэтому приведем окончательный результат:

, .

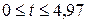Постоянные интегрирования 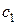и 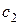найдем из начальных условий 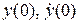, предварительно выразив :

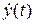Отсюда

В конце первого этапа при продажа товара характеризуется параметрами . Они будут служить начальными условиями для второго этапа.

На втором этапе решается дифференциальное уравнение

,

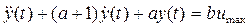с начальными условиями . Решение находится аналогично примеру 3.3:

.

Постоянные интегрирования и вычисляются из системы уравнений:

В итоге

В конце второго этапа при продажа товара характеризуется параметрами 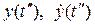. Они будут служить начальными условиями для третьего этапа.

На третьем этапе решается дифференциальное уравнение

,

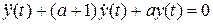с начальными условиями 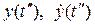. Общее решение имеет вид

.

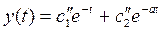Постоянные интегрирования 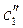и находятся из системы уравнений:

Они имеют вид:

Дата добавления: 2014-11-29