Решение задачи методом динамического программирования

1. Этап попятного движения.

Шаг 1. От управляющего воздействия 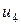зависит только последнее слагаемое в показателе качества 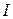, поэтому минимизацию показателя качества 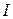по переменной 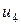можно провести отдельно, независимо от других переменных, образовав для этой цели вспомогательный показатель качества

.

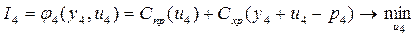Минимизацию показателя 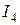можно провести только методом перебора, так как зависимость 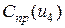задана табличным способом. Перебору подлежат состояние объекта 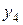и управляющее воздействие 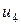. Состояние 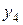должно изменяться в постоянных границах от 0 до 5000 изделий (емкость склада) с дискретностью 1000 изделий; управление 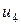будет иметь различные границы в зависимости от состояния 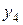, заявки потребителей 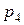, максимального месячного объема производства, емкости склада.

Так, например, если 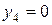, т.е. на складе к началу четвертого месяца нет запаса готовой продукции, то допустимыми являются управляющие воздействия 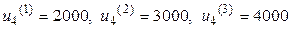. Первое значение определяется заявкой потребителей на 2000 изделий в этом месяце, последнее значение – максимальным месячным объемом производства. Вычислим значения показате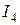ля для 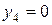и допустимых управлений:

,

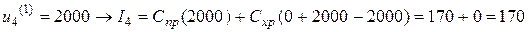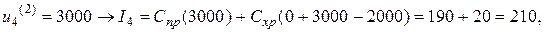
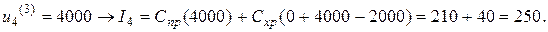Минимальное значение показателя 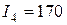достигается при 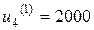; эти значения заносим в первую строку табл. 2.

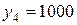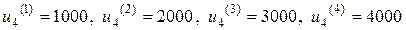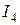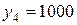Рассмотрим следующее возможное состояние (на складе имеется готовая продукция в количестве 1000 изделий). Допустимыми являются управления . Вычислим показатель для и допустимых управлений:

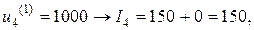
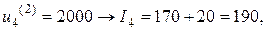
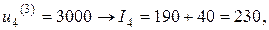
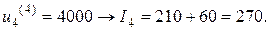
Минимальное значение показателя 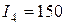достигается при 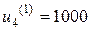; эти значения заносим во вторую строку табл. 2.

Для состояния объекта 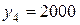допустимыми являются управления 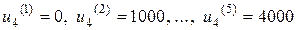. Минимальное значение показателя 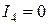достигается при 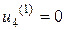; эти значения заносим в третью строку табл. 2.

Для состояния объекта 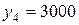допустимыми являются управления 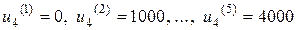. Минимальное значение показателя 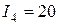достигается при 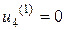; эти значения заносим в четвертую строку табл. 2.

Для состояния объекта 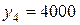допустимыми являются управления 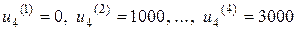. Управление 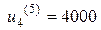не является допустимым, так как величина 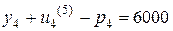превышает емкость склада. Минимальное значение показателя 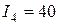достигается при 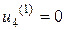; эти значения заносим в пятую строку табл. 2.

Для состояния объекта 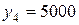допустимыми являются управления 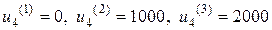. Управления 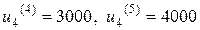не являются допустимыми из-за превышения емкости склада. Минимальное значение показателя 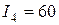достигается при 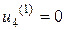; эти значения заносим в шестую строку табл. 2.

Таблица 2 (для момента 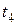) Таблица 3 (для момента t ₃)

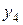
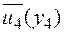
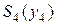
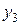
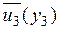
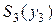
Шаг 2. Заметим, что от управлени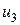й и 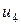зависят только два последних слагаемых в показателе качества I, поэтому минимизацию показателя качества по этим управлениям можно провести независимо от остальных управлений, образовав для этой цели вспомогательный показатель качества

.

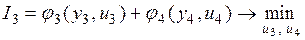От управления 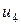здесь зависит только последнее слагаемое, минимизация которого была проведена на предыдущем шаге. Заменим последнее слагаемое его минимальным значением 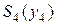и с помощью разностного уравнения ОУ выразим состояние 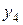в виде 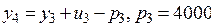. В итоге получим:

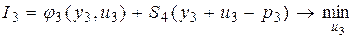
или в развернутой форме

.

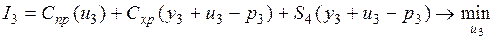Показатель качества 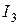зависит от одной переменной 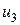, что существенно упрощает процедуру его минимизации. Результаты минимизации показателя 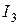занесем в табл. 3. Этой таблице предшествовали следующие вычисления, также основанные на методе перебора.

Если y₃ =0 (готовой продукции на складе нет, а заявки в этом месяце составляют 4000 изделий), то допустимым является одно управление 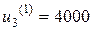, при котором вспомогательный показатель качества

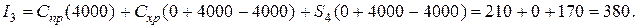
Здесь последнее слагаемое 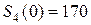берется из предыдущей таблицы. На основании этих вычислений формируем первую строку таблицы.

Если y₃ =1000, то допустимыми являются управления 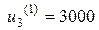и 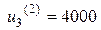. Вычислим значения показате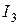ля для 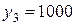и допустимых управлений:

,

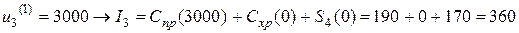. Выбираем минимальное значение показателя 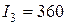и соответствующее оптимальное управление 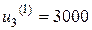, которые заносим во вторую строку таблицы.

Аналогичным образом заполняем остальные строки таблицы.

Шаг 3. Заметим, что от управлений 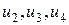зависят только три последних слагаемых в показателе качества I, поэтому минимизацию показателя качества по этим переменным можно провести независимо от остальных переменных, образовав для этой цели вспомогательный показатель

.

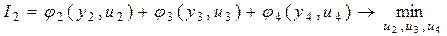От управлений u₃ и u₄ здесь зависят только два последних слагаемых, минимизация которых была проведена на предыдущем шаге. Заменим эти слагаемые их минимальным значением 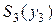, т.е.

,

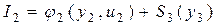а состояние 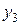на основании разностного уравнения представим в виде 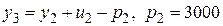. В итоге получим:

или в развернутой форме

.

Показатель качества 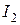снова зависит от одной переменной .

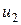Результаты минимизации показателя качества 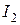занесем в табл. 4.

Таблица 4 (для момента )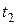

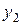
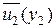
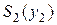
Этой таблице предшествовали вычисления, также основанные на методе перебора. Например, для y₂ =0 (готовой продукции на складе нет, а заявки в этом месяце составляют 3000 изделий) допустимыми являются управления 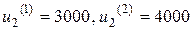, при которых показатель качества 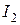принимает значения:

,

.

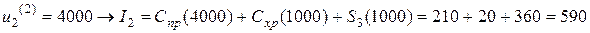Минимальное значение показателя 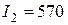и соответствующее оптимальное управление 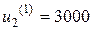занесем в первую строку таблицы.

Аналогичным образом заполняем остальные строки таблицы.

Шаг 4. Отступим на последний шаг от конца интервала управления и рассмотрим исходный показатель качества

.

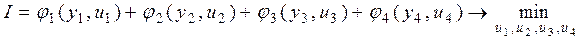От управлений u₂, u₃ и u₄ здесь зависят только три последних слагаемых, минимизация которых была проведена на предыдущем шаге. Заменим эти слагаемые их минимальным значением 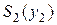, т.е.

,

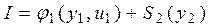а состояние 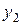на основании разностного уравнения представим в виде 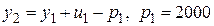. В итоге получим:

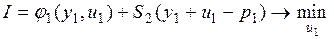
или в развернутой форме

.

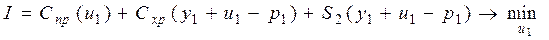Минимизация этого показателя качества проводится только для начального состояния ОУ, т.е. для 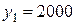. Допустимыми являются управления 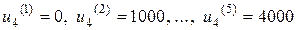. Вычислим значения показате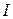ля для 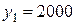и допустимых управлений:

,

,

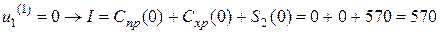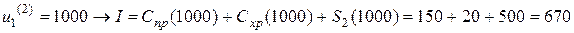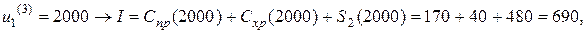
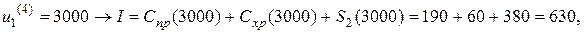
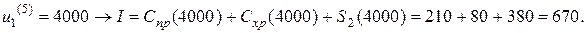
Минимальное значение показателя качества 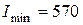соответствует всей процедуре управления, содержащей 4 шага. Оптимальное управление на 1 шаге 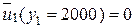. Оптимальные управления на остальных шагах еще не известны, но минимальное значение показателя качества найдено для всей задачи. Такова особенность последнего шага попятного движения.

Дата добавления: 2014-11-29