Проверка нормальности распределения

Необходимо провести проверку соответствия распределения результатов измерения контролируемого параметра, представленных в предыдущем параграфе (Таблица 3) нормальному закону распределению.

Фрагмент электронной таблицы с исходными данными представлен на Рисунок 34.

Для проверки соответствия распределения результатов тестового контроля нормальному закону, будем использовать модуль «Distribution Fitting» (апроксимация распределения).

Для запуска модуля выполнить «Statistics»®«Distribution Fitting» (Рисунок 22).

В появившемся окне выбора аппроксимируемого распределения (Рисунок 44) выбрать раздел «Continuous Distributions» (непрерывные распределения) и в нем выбрать «Normal» (нормальное распределения), после чего нажать кнопку «OK».

В следующем окне (Рисунок 45) необходимо задать переменную, в которой находятся исследуемые данные. В нашем случае это переменная «Рез-т измер.».

Далее на закладке «Parameters» указать параметры аппроксимации распределения:

1) Number of categories – количество интервалов группировки исходных данных;

2) Lower limit – нижняя граница интервала группировки исходных данных;

3) Upper limit – верхняя граница интервала группировки исходных данных;

4) Mean – вычисленное среднее выборочное значение исходных данных;

5) Variance – вычисленное значение дисперсии исходных данных.

В большинстве случаев система сама устанавливает оптимальные значения данных параметров, но при необходимости их можно изменить.

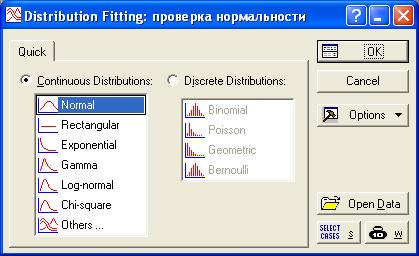
Рисунок 44 - Окно выбора аппроксимируемого распределения

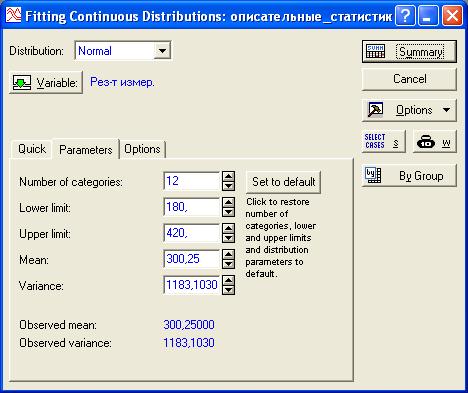
Рисунок 45 - Окно задания исходных данных и параметров аппроксимации распределения

На вкладке «Options» (опции) окна задания исходных данных и параметров аппроксимации распределения (Рисунок 46) выбрать критерий оценки соответствия распределения исследуемых данных нормальному закону («Kolmogorov-Smirnov test» – вычисление критерия Колмогорова-Смирнова и/или «Chi-Square test» - вычисление критерия Пирсона 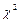), и способ графического представления результатов подгонки распределения [представление на графике фактического распределения частот («Frequency distribution») или накопленных сумм частот (Cumulative distribution) попадания результатов наблюдений в интервалы], а также способ разметки оси частот («Raw frequencies» - фактическая частота либо «Relative frequencies (%)» - относительная частота).

Если поставить флажок напротив опции «Combine categories» то система будет объединять в которые попало менее 5 результатов наблюдений с близлежащими категориями.

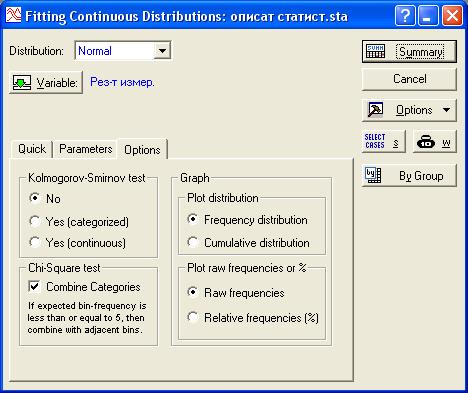
Рисунок 46 - Вкладка «Options» задания исходных данных и параметров подгонки распределения

Для проведения анализа выберем критерий Пирсона («Chi-Square test»). В разделе задания параметров графического отображения результатов анализа выберем представление на графике фактического распределения частот попадания результатов наблюдений в интервалы («Frequency distribution»), а способ разметки оси частот - фактическая частота («Raw frequencies»), как это показано на Рисунок 46.

Для вывода на экран результатов анализа, на вкладке «Quick» нажать кнопку .

В результате появится таблица, результаты группировки данных по интервалам и соответствующие им ожидаемые частоты, предсказанные нормальным распределением (Рисунок 47).

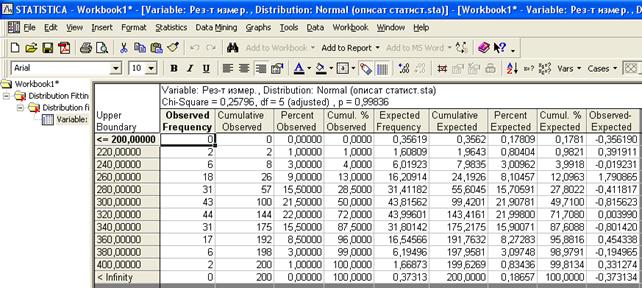
Рисунок 47 - Табличные результаты аппроксимации распределения

В этой таблице:

1) Observed Frequency –частота наблюдений, попавших в интервал;

2) Cumulative Frequency - частота наблюдений, попавших в интервал с накоплением;

3) Percent Observed – процент наблюдений, попавших в интервал;

4) Cumul. % Observed – процент наблюдений, попавших в интервал с накоплением;

5) Expected Frequency – предсказанная частота наблюдений, попавших в интервал в соответствии с нормальным законом распределения;

6) Cumulative Expected – предсказанная частота наблюдений, попавших в интервал с накоплением, в соответствии с нормальным законом распределения;

7) Percent Expected – предсказанный процент наблюдений, попавших в интервал в соответствии с нормальным законом распределения;

8) Cumul. % Expected – предсказанный процент наблюдений, попавших в интервал с накоплением, в соответствии с нормальным законом распределения;

9) Observed- Expected – разность между частотой наблюдений, попавших в интервал и предсказанной частотой наблюдений, в соответствии с нормальным законом распределения.

Над таблицей (Рисунок 47) указано вычисленное значения критерия Пирсона 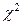(Chi-Square), число степеней свободы (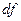) и уровень его значимости ().

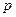Соответствие распределения исследуемых данных нормальному закону можно установить, сравнив вычисленное значение критерия Пирсона с табличным значением на требуемом уровне значимости. Если вычисленное значение меньше табличного, то распределение результатов наблюдений подчиняется нормальному закону распределения.

Для вывода на экран результатов анализа в графической форме, на вкладке «Quick», нажать кнопку .

В результате появится гистограмма, на которой красной цветом отображен график нормального распределения (Рисунок 48).

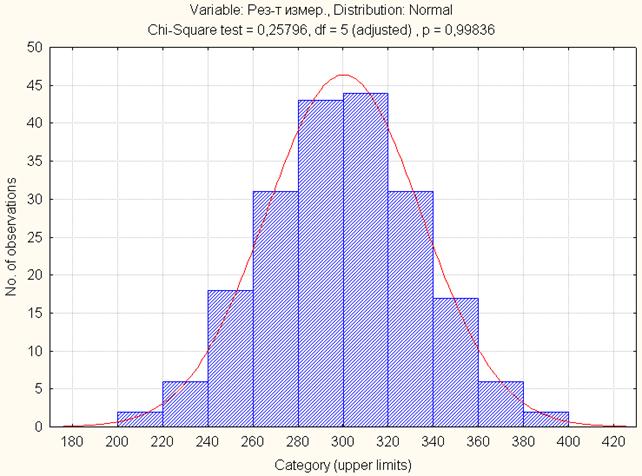
Рисунок 48 - Графические результаты аппроксимации распределения

Над графиком (рисунок 2.9) указано вычисленное значения критерия Пирсона 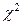(Chi-Square), число степеней свободы (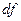) и уровень его значимости ().

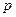Из графика также видно, что распределение исследуемых данных достаточно близко к нормальному закону.

Дата добавления: 2014-11-29