Решение. Действия над матрицами и их свойства

Свойства операций

Решение.

Решение.

Свойства операций

Действия над матрицами и их свойства

1) Суммой двух матриц 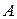и 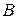одного и того же размера 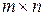называется матрица 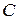того же размера, элементы которой равны суммам соответствующих элементов данных матриц, т.е.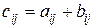 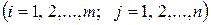. Операция вычисления матрицы 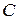называется сложением матриц 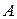и .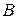

1^о .

2^о .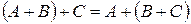

3^о .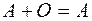

Пример 2.1. Найти сумму матриц 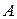и 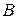, если

, .

.

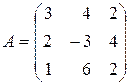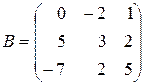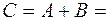
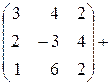
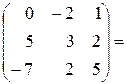
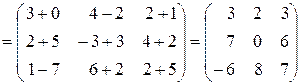2) Произведением матрицы 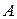на число 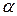называется матрица 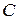, элементы которой есть элементы матрицы 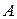, умноженные на 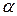, т.е. .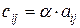

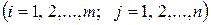Пример 2.2. Найти 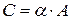, если , .

.

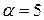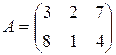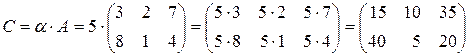1^о .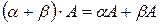

2^о .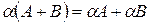

3^о .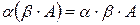

3) Разность двух матриц 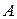и 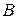одинаковых размеров определяется равенством .

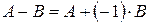Пример 2.3. Найти разность матриц:

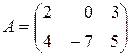и .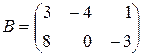

.

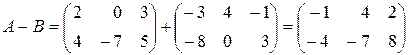4) Произведением матрицы 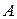размерности 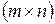на матрицу 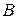размерности 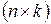называется матрица 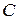размерности 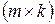, каждый элемент которой равен сумме произведений элементов 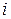-той строки матрицы 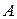на соответствующие элементы 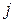-того столбца матрицы .

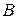Замечание: Правило умножения матрицы 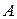на матрицу 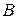определяется только для случая, когда число столбцов матрицы 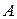равно числу строк матрицы .

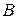Поясним правило умножения матриц примерами. Для начала покажем умножение строки на столбец:

,

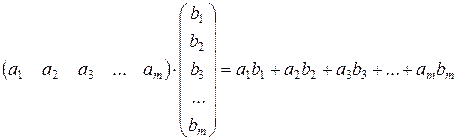т.е. их результат есть число. Аналогичным образом находится каждый элемент матрицы. Например, требуется перемножить матрицы

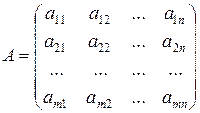и .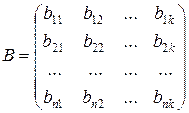

В результате получим матрицу

,

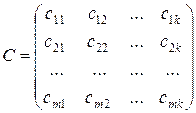каждый элемент которой мы находим по формуле

,

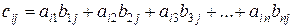то есть для того, чтобы найти элемент 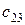мы элементы второй строки матрицы 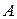умножаем на элементы третьего столбца матрицы 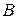и складываем между собой.

Примеры 2.4.:

а) .

б)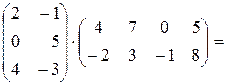

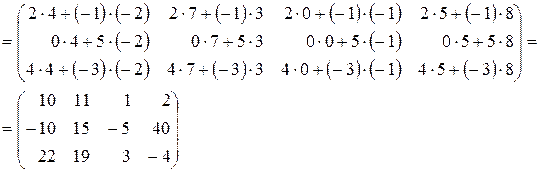
в) Даны матрицы 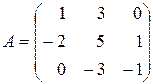и 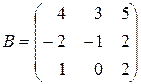. Найти матрицу .

.

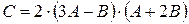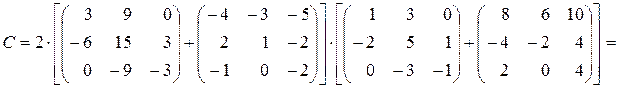
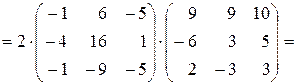
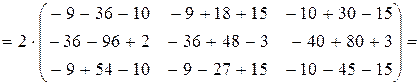
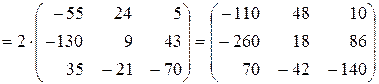Дата добавления: 2014-11-29