Методы вычисления определителя третьего порядка

Определители и способы их вычисления

Определитель – это число, соответствующее квадратной матрице, вычисленное определенным образом.

Определителем второго порядка называется число, определяемое равенством:

.

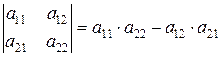Пример 3.1.

.

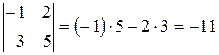Определителем третьего порядка называется число, определяемое квадратной матрицей третьего порядка.

1. Метод треугольников (метод Саррюса)

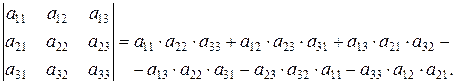
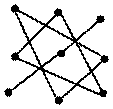
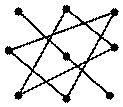
То есть, если элементы определителя третьего порядка записать в таблицу 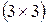, то правило его вычисления может быть представлено на рисунке 1, и определитель будет равен алгебраической сумме всех произведений, причем произведения первой таблицы берут со знаком “+”, а второй – со знаком “–”.

Рис. 1

Это правило называется правилом Саррюса.

2. Метод дописывания двух столбцов.

Этот способ вычисления определителя третьего порядка заключается в дописывании первых двух столбцов определителя и нахождении суммы произведений по главной диагонали и параллелях к ней за вычетом суммы произведений побочной диагонали и параллелях к ней, т.е.

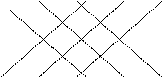
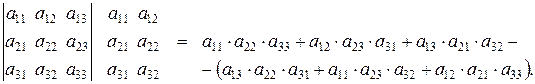
Пример 3.2. Вычислить определитель двумя способами

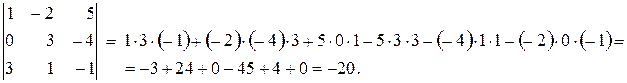
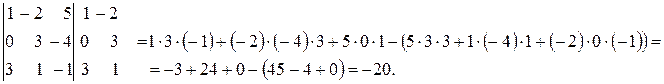
3. Третий способ вычисления определителя основан на теореме разложения.

Минором элемента определителя 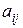называется определитель, полученный из данного путем вычеркивания 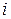-й строки и 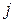-го столбца, на пересечении которых расположен этот элемент.

Например, минором элемента 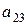определителя

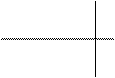
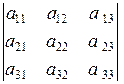
является определитель

,

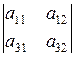т.е. из исходного определителя были вычеркнуты вторая строка и третий столбец.

Алгебраическим дополнением 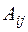элемента 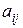называется минор этого элемента, умноженный на 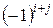. То есть, если сумма номеров строки и столбца, на пересечении которых стоит этот элемент является четным числом, то минор берут со знаком “+”, а если нечетным, то со знаком “–”.

При этом полезно иметь в виду следующую схему:

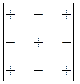
где знаком плюс отмечены места тех элементов, для которых алгебраические дополнения равны минорам, взятым с их собственным знаком; и знаком минус те, для которых алгебраические дополнения равны минорам, взятым с противоположным знаком.

Теорема разложения

Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.

Пример 3.3. Вычислить определитель путем разложения: а) по второй строке; б) по третьему столбцу.

а)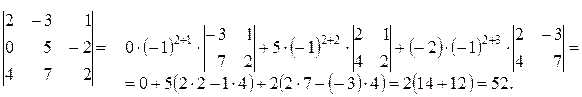

б)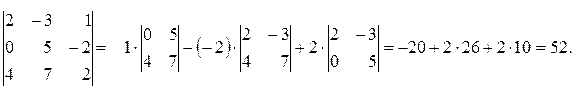

Замечание. Если в задании не указано, по какому столбцу (строке) проводить разложение, то лучше выбирать столбец (строку) с большим числом нулей.

Определитель 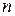-го порядка задается квадратной таблицей чисел (элементов определителя), имеющей 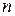строк и 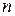столбцов, обозначается символом

.

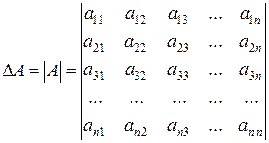Вычисление определителей порядка больше 3, рекомендуется проводить с помощью теоремы разложения.

Дата добавления: 2014-11-29