
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Негізгі таратылатын материалдар тізімі 3 страница
|
|
|
|
Сенімділік интервалдар мен сенімділік ықтималдылығын жалпылама бағалау үшін кіші таңдама нәтижесі бойынша тығыздығы мына түрде берілетін Стьюдент үлестірімі қолданылады:
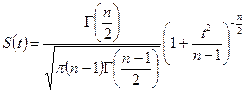 (52)
(52)
Мұнда, п – берілген таңдамағы сан, 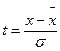 ;
; 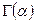 –
–  аргументтен гамма-функция.
аргументтен гамма-функция.
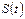 функциясы
функциясы 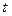 -ның бірдей оң және теріс абсолютті мәні бойынша бірдей, яғни симметриялы ж/е
-ның бірдей оң және теріс абсолютті мәні бойынша бірдей, яғни симметриялы ж/е 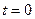 болғанда максимум болады,
болғанда максимум болады, 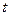 -ның абсолютті мәнінің өсуі кезінде функция асимптотиялық нольге жақындайды.
-ның абсолютті мәнінің өсуі кезінде функция асимптотиялық нольге жақындайды.  (> 20
(> 20 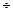 30) болғанда Стьюдент үлестірімі нормальды үлестірімге өтеді, керісінше п азайғанда айырмашылық өседі. Көрсеткішті үлестірім шұғыл ассиметриялы болып табылады және мына дифференциалды функциямен өрнектеледі:
30) болғанда Стьюдент үлестірімі нормальды үлестірімге өтеді, керісінше п азайғанда айырмашылық өседі. Көрсеткішті үлестірім шұғыл ассиметриялы болып табылады және мына дифференциалды функциямен өрнектеледі:
 (53)
(53)
Х-тек оң шама ғана бола алады. (X>0). Бұл үлестірімнің ерекшелігін мына қатынаспен көрсетеді:
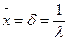 (54)
(54)
Көрсеткішті үлестірімнің интегралды функциясы:
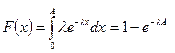 (55)
(55)
Көрсеткішті заң деп, әдетте көптеген детальдардан құрылған әртүрлі күрделі құрылғылардың (механизм, аспаптар, станоктар) істен шығуына жасалған үлестірілімді сипаттау қабылданады.
"хи-квадрат" үлестірімі дифференциалдық функциямен сипатталады.
 (56)
(56)
Здесь 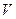 -величина, распределенная по закону "хи-квадрат", причем
-величина, распределенная по закону "хи-квадрат", причем  ,
, 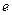 - основание натуральных логарифмов
- основание натуральных логарифмов 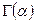 -гамма-функция, К -число степеней свободы:
-гамма-функция, К -число степеней свободы:
мұнда: V – 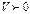 кезінде хи-квадрат заңы бойынша үлестірілген шама;
кезінде хи-квадрат заңы бойынша үлестірілген шама;
е –  гамма функциясы натуралды логарифмнің негізі;
гамма функциясы натуралды логарифмнің негізі;
К – еркіндік дәрежесінің саны:
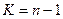 (57)
(57)
хи-квадрат үлестірімі таңдамадағы мүшелер санына тәуелді. Оған мына қатынас лайық:
 (58)
(58)
мұнда: k – орташа мән;
D – дисперсия.
Кіші К үшін үлестірім өткір ассиметрияны, мүшелер санының өсуіне қарай ассиметриялық қасиет азаяды.  кезінде хи-квадрат үлестірімі нормальды үлестірімге өтеді.
кезінде хи-квадрат үлестірімі нормальды үлестірімге өтеді.
Үлестірімнің интегралды функциясының түрі мынадай:
 (59)
(59)
НЕГ 1 [97-112 бет], ҚОС 5 [26-36 бет]
Бақылау сұрақтары:
1. Кәдімгі орналастыру заңының қасиеттері?
2. Кәдімгі логарифмдік орналасу заңы қашан қолданылады?
3. Қандай үрдістер Стьюдентті орналастырумен сипатталады?
4. Қандай үрдістер орналасу көрсеткіштерімен сипатталады?
5. Қандай жағдайларда «хи-квадрат» орналасуы нақты орналасуға ауысады?
Дәріс 6. Таңдама сипаттамасының дәлдігі
Таңдама сипаттамасы (орташа мән, стандартты ауытқу, мода, қарқын, интервалдық бөлінді және т.б.) бас жиынтықтың сипаттамасынан өзгеше.  таңдаманың аттас сипаттамасы мен
таңдаманың аттас сипаттамасы мен 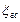 бас жиынтық айырмасы таңдама сипаттамасының қатесі деп аталады.
бас жиынтық айырмасы таңдама сипаттамасының қатесі деп аталады.
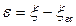 (60)
(60)
Бас жиынтық сипаттамасы белгісіз болғандықтан  қатені табу қиынға соғады. Бұл есепті шешу таңдау сипаттамаларын кездейсоқ шамалар ретінде қарастыру арқылы жүзеге асады.
қатені табу қиынға соғады. Бұл есепті шешу таңдау сипаттамаларын кездейсоқ шамалар ретінде қарастыру арқылы жүзеге асады.
Белгілі бір бас жиынтықтан 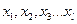 (
( - таңдама саны) алынған бірнеше таңдаманың орташа мәндерімен тұратын қатар бар деп есептейік.
- таңдама саны) алынған бірнеше таңдаманың орташа мәндерімен тұратын қатар бар деп есептейік.
Бұл қатар үшін 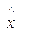 орташа мәнді («орташалардың орташасы») табуға (қатардағы (4.3) берілгендердің жеткілікті санымен оның бас жиынтықтың орташа мәнінен айырмашылығы өте аз) және
орташа мәнді («орташалардың орташасы») табуға (қатардағы (4.3) берілгендердің жеткілікті санымен оның бас жиынтықтың орташа мәнінен айырмашылығы өте аз) және  стандартты ауытқуды табуға болады.
стандартты ауытқуды табуға болады.
І реттік нөмірлі таңдама бойынша
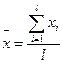 ;
;  (61)
(61)
 орташа мәннің қатесі (60) келісе отырып, мынадай болады:
орташа мәннің қатесі (60) келісе отырып, мынадай болады:
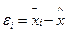 (62)
(62)
Міндет, бір ғана таңдаманың деректері бойынша қате шаманы алуға тырысу. Бұл жағдай үшін дәлелденгені
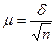 (63)
(63)
Мұнда  -таңдама мүшелерінің стандартты ауытқуы, п- оның көлемі. Жалғыз ғана таңдамадан
-таңдама мүшелерінің стандартты ауытқуы, п- оның көлемі. Жалғыз ғана таңдамадан 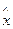 анықтау мүмкін емес, олай болса, нақты шаманы да,
анықтау мүмкін емес, олай болса, нақты шаманы да,  қате белгісін де табу мүмкін емес. Алайда оның максималды мүмкін
қате белгісін де табу мүмкін емес. Алайда оның максималды мүмкін 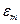 абсолютті мәнін табуға болады, олай болса,
абсолютті мәнін табуға болады, олай болса,
 (64)
(64)
Ішінен жеке таңдама бойынша  үлестірімнің орташа мәні Стьюдент үлестірім заңына әрқашанда бағынатындығы дәлелденген. (64)- тен шығатыны:
үлестірімнің орташа мәні Стьюдент үлестірім заңына әрқашанда бағынатындығы дәлелденген. (64)- тен шығатыны:
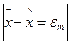 (65)
(65)
немесе, Стьюдент функциясының 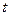 аргументін ескере отырып:
аргументін ескере отырып:
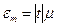 (66)
(66)
(6) ескере отырып, жазамыз:
 (67)
(67)
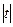 -ны анықтау үшін, (64) қатынасы әділ болуы үшін
-ны анықтау үшін, (64) қатынасы әділ болуы үшін 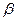 сенімділігін беру қажет. Оның үстіне Стьюденттің үлестірім интегралды функциясы мынадай:
сенімділігін беру қажет. Оның үстіне Стьюденттің үлестірім интегралды функциясы мынадай:
 (68)
(68)
әрі қарай да 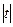 -ны п таңдама көлемін ескеретін кестеден табады.
-ны п таңдама көлемін ескеретін кестеден табады.
Осылайша 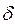 таңдаманың стандартты ауытқуы,
таңдаманың стандартты ауытқуы, 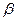 сенімділік үлкен болған сайын және п көлем кіші болған сайын орташа мән қатесі үлкен болады. Орташа мән қатесі берілген
сенімділік үлкен болған сайын және п көлем кіші болған сайын орташа мән қатесі үлкен болады. Орташа мән қатесі берілген 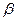 сенімділігі мен
сенімділігі мен 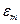 берілген мәннен асып түспеуі үшін қажет таңдама көлемін (67) теңдеуінен табуға болады.
берілген мәннен асып түспеуі үшін қажет таңдама көлемін (67) теңдеуінен табуға болады.
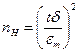 (69)
(69)
Бұрғылаудағы ғылыми зерттеу тәжірибесінде әртүрлі ескі және жаңа техникалардың сынақтарының нәтижелерін салыстырып бағалау жүргізуге тура келеді.
Егер салыстыру жаңа техниканың пайдасына шешілсе, бірақ оның артықшылығы айтарлықтай болмаса, онда бұл артықшылық кездейсоқ емес пе деген сұрақ туады. Жаңа құрылғының артықшылығының маңызын тексеру қажет.
Математикалық есеп мына түрде беріледі:
Екі таңдама бар:  және
және 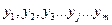
Таңдаманың орташа мәні және оған сәйкес стандартты ауытқулар 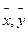 және
және 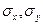 . Егер бір бас жиынтықтың екі таңдама бойынша орташа мәні болса,
. Егер бір бас жиынтықтың екі таңдама бойынша орташа мәні болса,  пен
пен  арасындағы айырмашылық маңызды емес. Егер таңдамалар әртүрлі бас жиынтықтарға жататын болса (кері гипотеза), онда айырмашылық елеулі болады. Егер сенімділігі
арасындағы айырмашылық маңызды емес. Егер таңдамалар әртүрлі бас жиынтықтарға жататын болса (кері гипотеза), онда айырмашылық елеулі болады. Егер сенімділігі 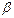 берілген мәннің
берілген мәннің  сенімділігінен кем болмаса қабылдайтын тура гипотезаны қарастырады. Егер тура гипотеза сенімділігі жеткіліксіз болса, онда бұл гипотезаны теріске шығарады және елеулі айырмашылықтың дәлелі ретінде кері гипотеза қабылданады.
сенімділігінен кем болмаса қабылдайтын тура гипотезаны қарастырады. Егер тура гипотеза сенімділігі жеткіліксіз болса, онда бұл гипотезаны теріске шығарады және елеулі айырмашылықтың дәлелі ретінде кері гипотеза қабылданады.  пен
пен  орташа мәндер арасындағы айырмашылық елеулі болуына кепілдік беру үшін
орташа мәндер арасындағы айырмашылық елеулі болуына кепілдік беру үшін  берілген мәнді өте төмен қабылдайды – шамамен 0,1 және одан да аз. Тура гипотезаны қарастыра отырып, бір басты жиынтықтан жасалған бірнеше таңдама бойынша орташа мәннің Стьюдент заңына сәйкес үлестірімі ескеріледі. Бұл заңға
берілген мәнді өте төмен қабылдайды – шамамен 0,1 және одан да аз. Тура гипотезаны қарастыра отырып, бір басты жиынтықтан жасалған бірнеше таңдама бойынша орташа мәннің Стьюдент заңына сәйкес үлестірімі ескеріледі. Бұл заңға  , да
, да  да бағынатын болғандықтан (к-ны таңдама бойынша орташа),
да бағынатын болғандықтан (к-ны таңдама бойынша орташа),
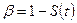 (70)
(70)
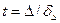 (71)
(71)
Осының ізімен
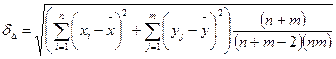 (72)
(72)
 мен
мен 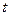 тауып
тауып  анықтайды, еркіндіктің дәреже саны ретінде мынаны қабылдайды
анықтайды, еркіндіктің дәреже саны ретінде мынаны қабылдайды
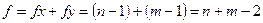 (73)
(73)
Егер екі таңдаманың әрбірі бойынша шама
10 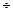 15тен асып түссе және
15тен асып түссе және  болса, онда
болса, онда  табу үшін қарапайымырақ формуланы қолдануға болады:
табу үшін қарапайымырақ формуланы қолдануға болады:
 (74)
(74)
мұнда:  пен
пен 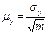
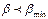 кезінде тура гипотеза теріске шығарады және
кезінде тура гипотеза теріске шығарады және
 и
и  арасындағы айырмашылықтың елеулілігі дәлелденген болып есептеледі, олай болмаған жағдайда айырмашылық елеулі емес деп ұйғарылады. Алайда бұл соңғы шешімді түпкілікті деп қарастыруға болады, себебі ол п мен m нен асып түспейтін таңдама көлемдеріне ғана лайық.
арасындағы айырмашылықтың елеулілігі дәлелденген болып есептеледі, олай болмаған жағдайда айырмашылық елеулі емес деп ұйғарылады. Алайда бұл соңғы шешімді түпкілікті деп қарастыруға болады, себебі ол п мен m нен асып түспейтін таңдама көлемдеріне ғана лайық. 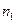 және
және 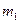 жаңа көлемдер алдыңғыдан
жаңа көлемдер алдыңғыдан 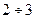 есе асып түскенше тәжірибені жалғастыра отырып,
есе асып түскенше тәжірибені жалғастыра отырып, 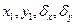 -ны қайта санап шығуға болады және тағы да бір рет келтірілген әдістемені қолдауға болады.
-ны қайта санап шығуға болады және тағы да бір рет келтірілген әдістемені қолдауға болады.
Таңдама дисперсиясының дәлдігінің бас жиынтық дисперсиянан қате шамасына айырмашылығы бар.
 (75)
(75)
 ақиқат шама белгісіз болғандықтан,
ақиқат шама белгісіз болғандықтан,  дәлдік мәнді анықтау да мүмкін емес, сондықтан қалыптасқан
дәлдік мәнді анықтау да мүмкін емес, сондықтан қалыптасқан 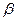 сенімділікпен
сенімділікпен  бас жиынтық дисперсиясы қорытындылатын шектерді табу міндеті тұрады.
бас жиынтық дисперсиясы қорытындылатын шектерді табу міндеті тұрады.
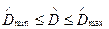 (76)
(76)
Егер бір бас жиынтықтан n көлемінің бірнеше таңдамасын жасаса, онда бір-бірінен айырмашылығы бар дисперсияның мәндері қатар құрады. Бұл қатар «хи-квадрат» үлестіріміне жауап беретіні дәлелденген, оның параметрі
 (77)
(77)
мұнда: 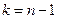 – еркіндік (бостық) дәрежелерінің саны.
– еркіндік (бостық) дәрежелерінің саны.
Үлестірме заңын біле отырып,  берілген сенімділік бойынша оған сәйкес
берілген сенімділік бойынша оған сәйкес 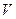 шамасының АВ сенімді интервалын құруға болады. А және В шектері үлестірімнің интегралды функциясының квантилдері болып табылады, А және В үшін мәндері тең.
шамасының АВ сенімді интервалын құруға болады. А және В шектері үлестірімнің интегралды функциясының квантилдері болып табылады, А және В үшін мәндері тең.
 (78)
(78)
А және В (77) формулаға қойып, аламыз:
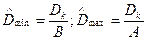 (79)
(79)
Дисперсияның максималды қатесі
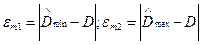 (80)
(80)
Максималды қателердің абсолютті мәні жоғары таңдама дисперсиясынан «хи-квадрат» үлестірімінің симметриялы толмағандығынан бірдей емес.
НЕГ 1 [112-124 бет], ҚОС 5 [36-46 бет]
Бақылау сұрақтары:
1. Таңдалған сипаттаманың қатесіне анықтама беру?
2. Таңдау қатесінің максимальді шамасы қалай анықталады?
3. Қандай көрсеткіштерден таңдау қатесінің шамасы тәуелді болады?
4. Екі, жаңа және ескі техникамен зерттеу нәтижелері бойынша айырмашылық негізі анықталады?
5. Орта мәнінің берілген сенімділік кезінде керекті шама қалай анықталады?
Дәріс 7. Бұрғылаудағы тәжірибелік тәуелділіктер
Ғылыми зерттеулер әдетте шамалар арасындағы тәуелділіктер құрумен байланысты. Тәуелділіктерді зерттеу нәтижелері бойынша олардың математикалық моделін (теңдеуін) жасайды, ол біреуінің белгілі мәні бойынша екіншісіне баға беруге мүмкіндік береді.
Нақты тәуелділіктерде, ереже бойынша, көп шамалар (факторлар) қатысады. Олар көп болған сайын математикалық модельді құру қиынырақ болады. Сондықтан алынған факторлардың ішінде маңыздысына көбірек көңіл бөлінеді. Қалған әсер ететін факторлар, шығарып алған тәуелділіктер әділ болатындай шарттар жиынтығы ретінде жұмыс істейді. Қарастыру екі шама арасындағы тәжірибелік тәуелділіктен басталып көп факторлы тәуелділікпен аяқталады.
Ғылымда бір-бірінен түбегейлі айырмашылығы бар екі зерттеу әдісі бар: теориялық және экспериментальды, яғни, тәжірибелік. Оларға тәуелділіктің екі түрі сәйкес келеді. Теориялық тәуелділікті шығаруға математикалық теңдеулердің көмегімен өрнектелген белгілі физика заңдары қолданылады. Егер қарастырылып отырған шамалардың қарым-қатынастарының физикалық мағынасы түсінікті болса теориялқ әдіс ыңғайлы болады, мұндай шамалар аз, әрі дәл бағалауға келмейді, яғни, кездейсоқтық элементі минимумға жақын келген жағдайда.
Кездейсоқтық элементі үлкен болған жағдайда, теориялық тәуелділіктер үлкен қиындықтар және қателермен түйіндестірілген. Мұндай жағдайда қарастырылып отырған процесс зерттеуші алдында табиғи күйінде (математикалық теңдеу күйінде емес) ұсынылатын зерттеудің тәжірибелік әдісін қолдану дұрыс.
Тәжірибелік әдіспен алынған нәтижелер өздері шығарылған шарттар кешеніне жиынтығына лайық. Мысалы, осьтік жүктеме және бұрғылау жылдамдығы арасындағы тәуелділік нақты жыныс түріне қарай сәйкес келеді, скважиналардың тереңдігі мен диаметрі, қалған режимдік параметрлердің шамаларының интервалдары мен коронка маркалары. Көрсетілген аралықтар ішінде шарт факторлары кездейсоқ өзгеруі мүмкін, мұндай кездейсоқтық қорытылған тәуелділікке әсерін тигізеді.
Кездейсоқтық элементін бейтараптандыру көптеген тәжірибені талап ететін математикалық статистика әдісімен жүзеге асады. Шамалар арасындағы тәуелділікті орнату тәжірибесі екі схеманың бірі бойынша жүргізіледі: регрессиялық және корреляциялық.
Регрессиялық схеманы кездейсоқ шаманың тәуелділігі кездейсоқ еместен алу қажет болғанда қолданады, яғни, тәжірибе жасаушы тәуелсіз шаманың кез келген қажетті мәнін талап ете алады. Бұл мәндер белгілі деңгейлер алып келеді (3-сурет). Жақын жатқанекі деңгейдің айырмашылығы қадам шамасына тең. әрбір деңгейде тәжірибелер бірнеше рет қайталанады, оның үстіне кездейсоқ мәннің әсерінен шамалар әртүрлі болып шығады. Регрессиялық схеманы пайдалану кезінде тәуелсіз шама – фактормен, ал тәуелді – нәтижемен немесе пікірмен белгіленеді.
Регрессиялық схеманы бұрғылау жылдамдығының тампонажды тастың мықтылығы режимінің параметрінен, қоспа құрамының маңызынан, тәуелділігін алмас коронкасы беріктігінің матрица қаттылығынан тәуелділігін орнату кезінде қолдануға болады.
Корреляциялық схеманы барлық қатысушылар шамаларына қарай кездейсоқ болғанда пайдаланады. Ол пассивті, яғни басқарылмайтын тәжірибеде ғана қолданылады. Бұл жағдайда сынақ жасаушы кездейсоқ пайда болған, өзара байланыстағы қос шаманы тіркеп, бақылайды. өздігінен ештеңе өзгерте алмайды (4-сурет). Көп жағдайда бақылап отырған шаманың қайсысы тәуелсіз, қайсысы тәуелді екені белгісіз (олардың бәрі фактор деп аталады). «Тәуелділік» деген ұғым мағынасын жоғалтады да, «байланыс» ұғымымен ауыстырылады.

 – факторлар деңгейі, – факторлар деңгейі, 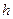 – қадам, – қадам, 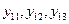 – бір деңгейде тәжірибені қайталау кезіндегі пікірлер (бағалар); – бір деңгейде тәжірибені қайталау кезіндегі пікірлер (бағалар); 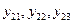 – бұл да 2-ші деңгейде; – бұл да 2-ші деңгейде;  – 1, 2, 3-ші деңгейдегі пікірлердің шартты орташа мәндері; – 1, 2, 3-ші деңгейдегі пікірлердің шартты орташа мәндері;  - интерполяция жолымен табылған пікір; - интерполяция жолымен табылған пікір; 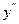 - экстраполяция жолымен табылған пікір.
3 сурет. Регрессиялық схема бойынша
орындалған тәжірибе. - экстраполяция жолымен табылған пікір.
3 сурет. Регрессиялық схема бойынша
орындалған тәжірибе.
| 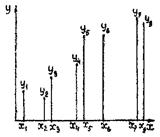
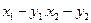 - өзара байланыстағы шамалардың қос мәндері.
4 сурет. Коррекциялық схема бойынша орындалған тәжірибе. - өзара байланыстағы шамалардың қос мәндері.
4 сурет. Коррекциялық схема бойынша орындалған тәжірибе.
|
Коррекциялық схема тау жыныстарының қаттылығы Коррекциялық схема тау жыныстарының қаттылығы мен абразивтілігі арасындағы бұрғылау валындағы айналу моменті мен скважинаның циркуляциялық жүйесіндегі қысым шығыны арасындағы (осындай қажеттілік пайда болғанда), бригаданың өнімділігі мен орташа жас құрамы арасындағы байланысты орнату кезінде қолданылады.
Тәуелділіктерді орнатудың әртүрлі әдістерінің өзара байланысы. Теориялық әдістің артықшылығы оның тәуелділік себептерін түсінуге және оның сипатын физикалық заңдылықтардың өзара әсері нәтижесі ретінде түсіндіруге мүмкіндік беретінін де. Екінші артықшылығы – салыстырмалы түрде аз шығындар, себебі стендлер, материалдар, энергия және т.б. қажеті жоқ. Теориялық тәуелділіктер дәлдігі ойға алған факторлармен олардың өзара әсері санымен шектеледі.
Экспериментальды әдістің басты артықшылығы зерттелетін нысананы танып білгенге байланысты емес. Тәжірибелік зерттеуден қол жеткізген дәлдік эксперимент көлемімен және бұл жағдай тәуелділік шығару кезіндегі шарттарға қаншалықты жақындығына байланысты.
Тәжірибелік тәуелділікті интерполяция мақсатында қолдану ыңғайлы, яғни сыналған деңгейлермен дәл келмегенмен зерттелген интервал ішінде жататын фактор мәндерінің нәтижелерін болжау. Интерполяция қатесі бағаланады және қажет болса минимумға тоғысады. Экстраполяция, яғни, тәжірибеден тыс жағдайда алынған тәуелділікті қолдану, құптарлық жағдай емес, себебі бағалауға келмейтін қателермен түйіндескен.
Теориялық және эксперименттік дістердің бірін-бірі толықтыруға ұмтылғаны қажет. Теориялық тәуелділіктерді тәжірибе нәтижелерін салыстыру арқылы тексереді. Бір жағынан теорияны алдын ала біліп алмай тәжірибені қою өте қиын.
Тәжірибелік тәуелділікті орнату схемасы арасында өтпес шекара жоқ. Мәселен, егер талап етілген фактор мәні тапсырмасының қателері көп болса, онда көршілес емес тап сол деңгейдің берілетіні туралы сенімділік жоғалады да, регрессиялық схема корреляциялыққа өтеді. Кейде, талап етілген тәжірибе көлемінің үлкендігіне қарамай корреляциялық схеманы регрессиялықты қолдануға болатын жерде пайдалану ыңғайлы. Бұл тәжірибені өндірісте өткізуге мүмкіндік береді.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 962; Нарушение авторских прав?; Мы поможем в написании вашей работы!