Негізгі таратылатын материалдар тізімі 4 страница

НЕГ 1 [125-129 бет], ҚОС 6 [3-7 бет]

Бақылау сұрақтары:

1. Зерттеудің теориялық әдісінің артықшылығы?

2. Зерттеудің тәжірибелі әдісінің артықшылығы?

3. Тәжірибені өткізудің регрессиялық әдісінің негізі?

4. Тәжірибені өткізудің корреляциялық әдісінің негізі?

5. Зерттеудің тәжірибелі әдістің кемшілігі?

Дәріс 8. Экспериментке дайындық және оның нәтижелерінің алдын ала сараптамасы

Тәжірибені жүргізу шарттары жиынтығының бағасы фактордың әрбір құрамы мәндерінің күтіліп отырған интервалдары түрінде беріледі. Жұмыс мазмұнына, бөлінген қаржы мен уақытқа қарап, тәжірибе активті немесе пассивті болама деген мәселені шешетін тәжірибелер тобын алдын-ала дайындайды. Факторлардың бағалау үшін өлшеу құралдары керек. Олардың шкала диапазондары бақыланатын факторлардың өзгеріс интервалдарымен сәйкес келуі қажет. Аспап қателігі мына түрде болу қажет.

, (81)

мұнда: – тәжірибе нәтижелерінің болуы мүмкін қатесі.

Регрессиялық схеманы қолдану кезінде алдымен мүмкін болатын фактор мәндерінің интервалын таңдайды.

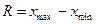, (82)

мұнда: 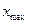және 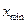– х фактордың барынша мүмкін мәндері.

Оларды есептер мен тәжірибе мүмкіндігіне қарап орнатады. Тәжірибе барысында фактор деңгейінің сыналу саны көп болған сайын, алынған тәуелділік дәлірек болады:

(83)

мұнда: 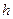– фактор өзгерісінің қадамы.

Деңгейлер саны ең аз мүмкін болатын қадамда көп болады.

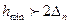(84)

Минималды – қажет деңгейлер саны қабылданатын моделінің түріне байланысты. Егер модель әдейі түзу сызықты болса, онда 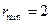. Жалпы жағдайда

(85)

мұнда: m – полином тәуелділігін өрнектейтін дәреже.

Регрессиялық схеманы қолдану кезіндегі тәжірибелердің жалпы саны:

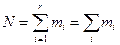(86)

мұнда: 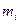– деңгейдегі тәжірибені қайталау саны.

Тәжірибе нәтижесі бойынша фактордың әрбір деңгейі үшін пікірдің орташа мәнін есептейді.

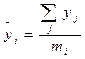(87)

мұнда: 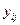– деңгейдегі 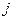тәжірибенің қайталану кезіндегі пікір мәні.

шартты орташа мән деп атайды, себебі фактор мәнін қабылдаған жағдайында мүмкін болады. Шартты орташа мәндерді тәуелділік сипатына алдын-ала баға бергенде пайдаланады.

Егер тәжірибе коррелациялық схема бойынша жүргізілсе, онда тәжірибелер қайталанбайды, шартты орташаны алу қиынға соғады. Алайда деректерді өңдеу кезеңінде корреляциялық схеманы регрессиялыққа корреляциялық кесте арқылы келтіруге болады. Оны тәжірибелер саны көп болған жағдайда қолдану мүмкін болады. 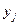Кестенің басы х шамасының интервалды вариациялық қатарын көрсетсе, бүйір жағы – y шамасын көрсетеді, және орташа интервалды мәндері берілген. 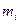және жиіліктің тәжірибенің әрбір интервалына түсетін саны – қосымша қатар мен бағанада көрсетілгенқатарлар мен бағаналардың қиылысында мен 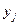бірігіп кездесуінің 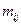жиіліктері берілген. мәні фактор деңгейі ретінде берілген және оған сәйкес келетін пікірлердің шартты орташа мәндері мен шартты дисперсияларды есептеуге болады.

(88)

Шамалар арасындағы байланыстың екі тарлық кретерийі бар: корреляция коэффициенті және корреляциялық қатынас. Екінші кретерийі дәлірек, бірақ тәжірибенің көп болғанын талап етеді.

Корреляция коэффициенті:

(89)

түрлендіруден кейін

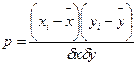(90)

мұнда: ( ) – х шамасының у көбейтіндісінің орташа мәні;

и – сәйкес шамалардың орташа мәндері;

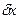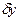және – орташа квадрат ауытқулар.

(91)

немесе 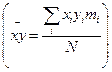(92)

Корреляция коэфициентінің мынадай қасиеттері бар:

Егер 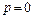болса, онда бірінші жуықтауда шамалар арасында байланыс жоқ деп ұйғарылады. Егер болса, онда шамалар функционалды түзу сызықты тәуелділікпен байланысты. 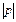үлкен болған сайын, байланыс тар болады. Егер 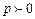болса, онда тәуелділік өскен сипатта болады. Егер 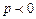болса, онда тәуелділік кемиді.

Қатал айтқанда, корреляция коэфициентін тек түзу сызықты тәуелсіздікке қолдануға болады. Корреляциялық қатынас тәуелсіздіктің кез келген түрінде байланысты көрсетеді.

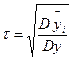(93)

мұнда: D_уі – пікірлердің шартты орташа мәндерінің дисперсиясы;

D_у – у шамасының жалпы дисперсиясы.

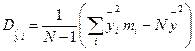(94)

Корреляция коэфицентіне қарағанда 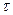әрқашанда оң.

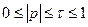(95)

Егер , шамалар арасында байланыс жоқ. Егер тәуелділік түзусызықты (пропорционалды) сипат алады. Қалған жағдайда және де айырмашылық үлкен болған сайын, түзусызықтан ауытқу көп.

Шартты дисперсияның біртектілігі

Тәжірибе кезінде оны өткізу шартының айтарлықтай өзгерістері болса, онда деректер біртекті болмайды. Ол, мысалы, тәжірибе деректері бірден емес бұрғылау жыныстарында фактордың әртүрлі деңгейі үшін таңдау алынған тұстакөрінер еді.

Деректердің біртекті еместігі Д; пікірлердің шартты дисперсиясы шамаларында көрінетіні дәлелденген. Дисперсияның біртектілігін Бартлер критериі бойынша тексереді.

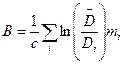(96)

Оның үстіне

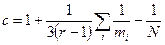(97)

мұнда: 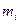– фактордың і деңгейіндегі тәжірибелердің қайталану саны;

r – осы деңгейлердің саны.

N – эксперимент көлемі. Орташа шартты дисперсия.

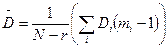(98)

В мәні т_i>2 кезіндегі кездейсоқ шама ретінде «хи-квадрат» үлестіріліміне бағынады. Егер дисперсия біртекті болса, онда бас жиынтыққа қатысты В=0 болады. Тәжірибе жүзінде табылған нөлден басқа В мәні елеусіз болады, ал шартты дисперсия біртекті болады, егер:

В<В_кр, (99)

Мұнда В_кр үлестірілім квантилі ретінде анықталады, интегралды функциясы 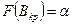, мұндағы еркіндік дәрежесі санында қабылданған мәнділік деңгейі.

НЕГ 1 [129-132 бет], ҚОС 6 [7-12 бет]

Бақылау сұрақтары:

1. Тәжірибені өткізу кезінде аспаптың максимальді қатесі қандай болу керек?

2. Тәжірибені өткізу кезінде фактордың шама бойынша өзгеруіндеминимальді қадам қандай болады?

3. Фактордың әр мәні кезінде үндеудің орта мәні қалай есептеледі?

4. Корреляция коэффициенті қалай анықталады?

5. Корреляциялық қатынас пен корреляциялық коэффициент арасындағы ұқсастығы және айырмашылығы неде?

Дәріс 9. Тік сызықты тәуелділік моделінің математикалық құрылымы

Теңдеу түрі:

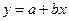(100)

Тік сызықты теңдеу бар.

а мен в коэффициенті тең екенін көрсетуге болады:

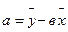(101)

Онда тік сызықты теңдеудің көрінісі:

немесе 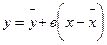(102)

Есептеу үрдісін жеңілдету мақсатында гиперболалық және экспоненциалдық тәуелдік тік сызыққа әкелуді көздейді. Гипербола үшін

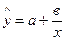(103)

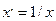теңдеуді қабылдайды, сонда 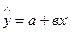(тік теңдеу).

(104)

Экспоненті бар болса, сызықтану логорифммен жетеді.

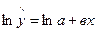(105)

мен 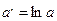қабылдап, нәтижесінде төмендегі теңдік анықталады.

(106)

Экспонент түрі

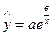(107)

Дәл осылай қала отырып, жаңа өзгермелі 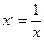қабылдап, нәтижесінде

(108)

Теңдігі орындалады.

Тік сызықты теңдеу дәлдігі

Кез келген тәжірибенің нәтижесі сияқты, регрессия коэффициенттері де кездейсоқ шама болып табылады. Төменде қарастырылған жағдайларда (және олар шындыққа жанасады) үндеулерді бөлу Стьюдент заңына бағынып, еркіндік дәрежесінің санына сай орындалады.

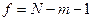(109)

мұнда: – тәжірибе көлемі;

– регрессия теңдеуінің дәрежесі.

Онда ауытқу кездейсоқ көлем төменгі теңдеумен анықталады.

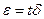(110)

мұнда: 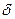– орта квадраттық ауытқу

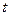– Стьюдентті бөлу функциясының квантилі.

Кездейсоқ шама аумағының екі жақты тежелуі (минимум мен максимум бойынша).

(111)

Ал шектеудің тек бір жағы қарастырылса (мысалы минимум бойынша), онда

(112)

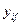Ауытқудың шегін сызық регрессияның табамыз. Дәлелдеу бойынша орта квадраттық ауытқу

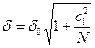(113)

мұнда: – былайша айтқанда «қалдық» орта квадраттық ауытқу

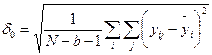(114)

Топтасқан мәліметтер үшін

(115)

Көрсеткіштер мәліметтер бойынша анықталады:

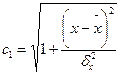(116)

(113) теңдеуден, орта мәнінен х фактор мәнімен анықталады. Ауытқу аймағының шегіне сәйкес кеңеді.

Регрессия теңдеуінің тәжірибесі бойынша 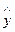мәні «негізгі» қате көлемінің мәнімен бекітіледі. Қате мәнінің максимальді мүмкіндігі 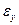төменгі теңдеумен анықталады

(117)

Онда орта квадраттық ауытқу ретінде

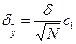(118)

Тәжірибе жүзінде алынған а және в коэффициенттернің мағынасы олардың салыстырмалы түрдегі негізгі мағынасы мына теңдеуде берілген, онда орта квадраттық ауытқу:

(119)

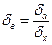(120)

НЕГ 1 [142-154 бет], ҚОС 6 [12-20 бет]

Бақылау сұрақтары:

1. Тік сызықты теңдеу регрессиясындағы коэффициенттер қалай анықталады?

2. Гиперболалық тәуелділік қалай тізбектеледі?

3. Экспоненциональді тәуелділік қалай тізбектеледі?

4. Үндеулердің жеке мағынасындағы шекті ауытқуларды регрессия сызығындағы ауытқулардан қалай ажыратамыз?

5. «Қалдық» орта квадраттық ауытқу қалай анықталады?

Дәріс 10. Параболалық тәуелділік моделінің математикалық құрылымы

Қисық сызықтың барлық тәуелділік түрлері: . Жоғарыда кез келген түрдің тәжірибелік тәуелділігі зерттеліп отырған құбылыстың физикалық жай күйіне байланысты болатынын айттық.

Тік сызықты тәуелділіктің қабылданбауының қажеттілігі мынаған негізделген

(121)

мұнда: 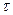– корреляциялық қатынас

р – корреляциялық коэффициент

– тәжірибе көлемі

– фактор деңгейінің саны.

F мөлшері алымның бос дәреже санымен Фишердің заңы бойынша дәлелденген

(122)

ал бөлімі

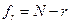(123)

Параболалық тәуелділікке көп санның екінші дәрежесі сәйкес келі керек

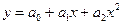
табу үшін, мына теңдеу жүйесін шешу керекрешают систему уравнений:

(124)

мұнда: – коэффициенттері корреляциялық кестенің көмегімен керекті тәжірибені өңдеуден кейін анықталады.

Қисық сызықты параболалық модельдердің дәлдігі

Регрессия сызығынан (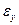) үндеудің үлкен мөлшердегі ауытқуын анықтау үшін мына шаманы қолданады.

(125)

мұнда: – регрессия сызығынан үндеудің қалдық орта квадраттық ауытқуы.

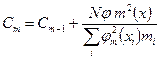(126)

Бұл мағына П.Л. Чебышевтің ортогональді полиномына кіреді, осыдан

(127)

Аталған мағыналар келесі түрде қолданады: ең алдымен (116) теңдеу арқылы алғашқы дәрежені теңестіру үшін С₁ анықталады, одан кейін (126) теңдеуі бойынша С₁ және С₃ көмегімен С₂ табылады. С₂, 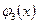С₄ және тағы басқаларын қолдана отырып, әрі кете береді, яғни регрессия теңдеуіне сай т дәрежесіне жеткенге дейін жүреді.

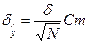(128)

Теңдеуді қолдана отырып, 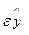максимальді қатесін (үндеудің ықтимал мағынасы) дәл табады.

НЕГ 1 [154-164 бет], ҚОС 6 [20-30 бет]

Бақылау сұрақтары:

1. Түзу сызықты тәуелдігінен бас тарту қай шамаға негізделіп жүзеге асырылады?

2. Регрессияның параболалық теңдеу коэффициентін қандай әдіс арқылы табады?

3. Регрессияның параболалық теңдеуінен үндеудің үлкен шамадағы ауытқуын қандай тәсілдер арқылы анықтайды?

4. Үндеу мағынасындағы мүмкін болатын максимальді қатені қалай табады?

5. Регрессия теңдеуінің коэффициентінде кездесетін қатені қалай анықтайды?

Дәріс 11. Көп факторлы тәжірибелі тәуелділіктер

Зерттелуші шама қашан да тек белгілі бір факторға (жоғарыда келтіргендей) ғана емес, оған әсер ететін үлкен кішілі факторларға тәуелді болады. Мысалы, бұрғылау режимінің көрсеткіштерімен, тау жынысын талқандаушы аспаптармен және тау жынысының қасиеттерімен тереңдік жылдамдығы байланысты, тәжірибелі математикалық модельге ие болу қажет. Көпфакторлы жағдайдағыдай математикалық модельдерді түрлі дәрежедегі көп мүшелі бейнеде елестеткен ыңғайлы. Регрессия теңдеуінің бірінші дәрежесінің түрі

(129)

Ал егер үш факторға ие болса (), онда төмендегідей болады.

(130)

Бірінші дәрежелі теңдеуді сызықты деп атайды, өйткені тек қана бір факторға ие болған теңдеу түзу сызықты теңдеуге сай келеді. 2 фактордың (алғашқы үш мүше) қатысуы жазықтық теңдеуіне, ал 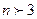геометриялық түсінігі қиындық тудырады. Регрессия теңдеуінің екінші дәрежесінің түрі мынадай

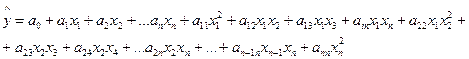(131)

Үш факторлар үшін мынаны аламыз

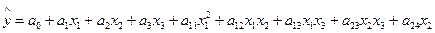(132)

(132) теңдеуін толық квадраттық модель деп атайды. Оның құрамына барлық жиынтық мүшелер кіреді, олардың дәрежесі т=2 аспайды. Бұл теңдеуде мүшелерінің дәрежесі бірге тең.

Көп факторлы модельдің геометриялық түсінігі мүмкін емес, себебі көп факторлы модельді таңдау оның физикалық табиғатына қайшы келеді. Алайда жоғарыда қарастырылған регрессияны (дәрежесі) тәжірибе нәтижесіне теңестірудің әмбебап статикалық критерийі өз күшін көп факторлы жағдайда да сақтап қалады. Әдетте статистикалық мағлұматты бірінші дәрежені теңестіруден бастайды, егер ол адекватты болмаса, регрессияның квадраттық дәрежесіне, кейін кубтық дәрежесіне және тағы басқа дәрежелеріне көтеріле береді.

Бір факторлы жағдайдағы секілді тәжірибе корреляциялы болмаса, регрессиялы кесте бойынша жүргізіледі. Тәжірибенің екі түрін жүзеге асырады. Олардың алғашқысын қолдану барысында тосыннан пайда болған факторлардың байланысы мен сол заңдылықққа жауап беретін үндеу мағынасын тіркеуге алады.

Регрессиялық кесте бойынша тәжірибе жүргізетін факторлардың белгілі бір тізбектегі сәйкестігін белгілейді, ал ондай тәжірибелердің нәтижесін алдын ала болжауға болады, сондықтан зерттеушілер керек нәтижеге қол жеткізу үшін барынша аз уақыт жұмыс жасайды. Барлық фактор үшін аумақты белгілейді, сол жерде ол зерттелуі тиіс. Ол интервалы арқылы беріледі. Оларды: сынды тізбекке бөледі. Егер зерттеу барысында барлық фактор бойынша мүмкіндігі мол дәреже сәйкестігін сынаса, онда мұндай зерттеу толық факторлы тәжірибе деп аталады. 1 кестеде үш факторға арналған толық факторлы тәжірибе берілген, мұнде біріншісі төрт деңгейге, екінші-үш, ал үшінші-екі деңгейге ие.

Дата добавления: 2014-11-29