Порядок выполнения лабораторной работы. Рисунок 2.1 - Симметричный доверительный интервал

.

,.

Рисунок 2.1 - Симметричный доверительный интервал

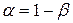- уровень значимости, вероятность того, что расхождения между параметром и его оценкой больше либо равно абсолютной величине доверительного интервала:

.

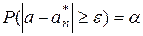Чаще всего .

Доверительный интервал – числовой интервал значений параметра ГС, которые не противоречат опытным данным или совместимы с опытными данными. Границы интервала и его величина получены по выборочным данным и поэтому случайны в отличие от самого параметра .

Величина доверительного интервала существенно зависит:

- от объема выборки (с ростом величина интервала уменьшается;

- от величины доверительной вероятности: чем больше доверительная вероятность 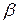, тем больше .

Оценка доверительного интервала для математического ожидания. Пусть для параметра генеральной совокупности получена доброкачественная оценка 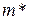. Нужно оценить полученную при этом ошибку «грубым» и «точным» методами. Определение 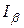возможно, если известен закон распределения статистической оценки, который зависит от закона распределения самой СВ, и от конкретного значения параметра ГС.

«Грубый метод» используется при следующих допущениях:

- допущение нормальности закона распределения СВ;

- замена параметров этого закона их статистическими оценками.

Пусть имеется случайная величина 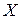– описывающая ГС, с неизвестными параметрами 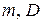. Найти доверительный интервал для , если задана доверительная вероятность и получены результаты эксперимента. Т.е., дано: 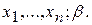Найти:

Известно, что статистическая оценка математического ожидания равна:

В качестве оценки реального по выборке принимается среднее арифметическое независимых наблюденных значений.

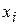– некоторый экземпляр случайной величины 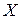с параметрами . Оценка - это сумма независимых одинаково распределенных СВ, тогда, по центральной предельной теореме при достаточно большом закон распределения этой суммы близок к нормальному.

В практической статистике даже при относительно небольшом числе испытаний (от 10 до 20) считается, что закон распределения стремится к нормальному. Тогда, вероятность попадания в интервал для нормального закона равна:

,

В симметричный интервал относительно :

.

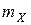Рассматриваемая СВ 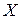- это оценка матожидания: ,

Величина доверительного интервала для матожидания равна (“грубый метод”):

где - квантиль нормального распределения. Тогда

.

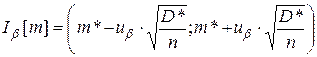Для примера 1 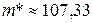, , 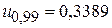. Тогда , , .

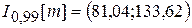Полученные с помощью «грубого» метода границы интервалов для математического ожидания, нанесем на полигон частот (см. рис. 2.2).

Рисунок 2.2 - Границы доверительных интервалов для мат. ожидания

“Точный ” метод оценки достоверности матожидания. Если 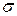не известно, то используют 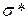и вместо нормального распределения 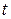-распределение Стьюдента:

,

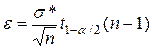где 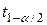- квантиль 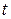-распределения (табличное значение).

Доверительный интервал для . Дана СВ 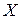с нормальным законом распределения и неизвестными параметрами и . Произведено независимых испытаний. Требуется по заданной доверительной вероятности найти доверительный интервал для .

В качестве оценки принимаем:

По аналогии с математическим ожиданием, оценка грубым методом:

, ,

Чтобы воспользоваться этими формулами вместо реальных и 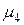пользуются их оценками:

Нормальный закон:

Равномерный:

Оценка «точным» методом: если известно, то

;

если неизвестно, то берут :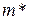

.

Контрольные вопросы

1. В чем разница между точечной и интервальной оценками?

2. Дайте определение медианы, моды, квантиля и процентиля.

3. Что такое мера достоверности и доверительный интервал?

4. Что такое мат. ожидание и дисперсия?

5. Чем «точный» метод оценки отличается от «грубого» метода?

1. По выборочным значениям из лабораторной работы 1 для своего варианта найти доброкачественные точечные оценки числовых характеристик параметров генеральной совокупности

2. Найти характеристики вариационного ряда для исследуемого признака: моду М_о, медиану , размах варьирования R, среднее абсолютное отклонение θ, коэффициент вариации V.

3. «Грубым» и «точным» методами получить интервальные оценки для 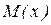и генеральной совокупности, задаваясь значениями доверительной вероятности .

4. Полученные границы интервалов для 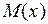, полученные «грубым» и точным методами нанести на полигоны частот или частостей.

Дата добавления: 2014-11-29