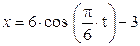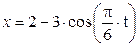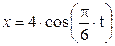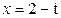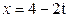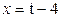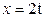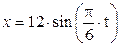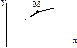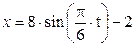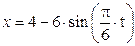Кинематика точки

КИНЕМАТИКА

Определить движение точки - это значит уметь определить положение точки по отношению к выбранной системе отсчета в любой момент времени.

В кинематике применяются три способа задания движения точки: векторный, координатный и естественный.

При векторном способе определения движения точки радиус-вектор движущейся точки М (рис. 21), проведенный из выбранного неподвижного центра О, выражается как векторная функция от времени, т. е.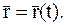

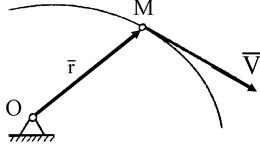
Рис. 21

Скорость 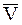точки, характеризующая быстроту и направление движения точки, равна производной по времени от ее радиуса-вектора:

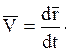
Ускорение 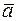точки, характеризующее изменение скорости по модулю и направлению, равно производной по времени от вектора скорости:

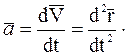
Координатный способ определения (задания) движения точки состоит в том, что координаты движущейся точки в выбранной системе координат выражаются как функции времени t.

Уравнения движения точки в декартовых координатах имеют вид

x = x (t), y = y (t), z = z (t).

Если точка движется в плоскости О ху, то будем иметь только два уравнения движения:

x = x (t), y = y (t).

Для того чтобы найти траекторию точки, достаточно из уравнений движения исключить время t. Вектор скорости и вектор ускорения определяются по их проекциям на оси декартовых координат, причем

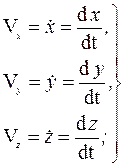
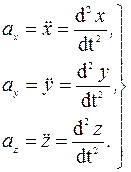
Отсюда получаем формулы разложения векторов скорости 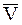и ускорения 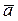по координатным осям:

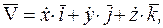
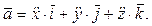
Модули векторов скорости и ускорения вычисляем по формулам

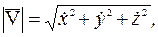
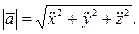
При естественном способе движение точки задается ее траекторией и уравнением движения по этой траектории:

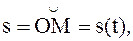
где О - начало отсчета дуг на траектории; s - дуговая координата точки М или взятая с соответствующим знаком длина дуги, отсчитываемая вдоль траектории от начала отсчета до точки М (рис. 22).

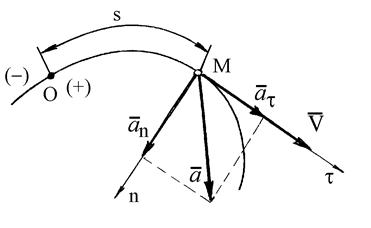
Рис. 22

Если заданы траектория движущейся точки и закон ее движения по этой траектории s = s (t), то вектор скорости направлен по касательной к этой траектории, а его проекция на направление касательной определяется по формуле

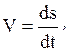
причем абсолютное значение этой проекции равно модулю скорости:

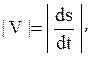
Вектор ускорения определяется по его проекциям на естественные оси (касательную, главную нормаль и бинормаль):

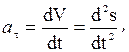
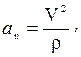
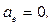
где r - радиус кривизны траектории в данной точке.

Следовательно,

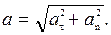
Отметим частные случаи:

1. Если точка движется прямолинейно и неравномерно, то радиус кривизны траектории r ® µ и, следовательно, а _n = 0. В этом случае ускорение направлено вдоль траектории точки и по модулю равно

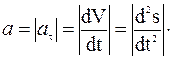
2. Если точка движется по криволинейной траектории равномерно, то

V = const и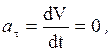

и поэтому ускорение направлено по нормали к траектории и по модулю равно

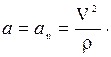
3. Если точка движется прямолинейно и равномерно, то a _n = 0, a _t = 0 и a = 0.

В том случае, когда движение точки задано в координатной форме, касательное ускорение определяется по формуле

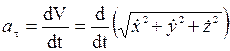, или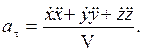

После этого нормальное ускорение можно найти из равенства

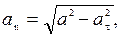
где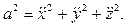

Определив 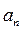, найдем радиус кривизны по формуле

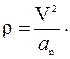
Если плоская траектория задана уравнением у = у (х), то радиус кривизны траектории вычисляется по формуле

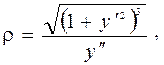
где 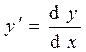и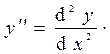

Задача K1

Точка M движется в плоскости ху (рис. K1.0–K1.9, табл. K1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями х = f ₁(t), у = f ₂(t), где х и у выражены в сантиметрах, t – в секундах.

Найти уравнение траектории точки; для момента времени t = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Зависимость х = f (t) указана непосредственно на рисунках, а зависимость у = f ₂(t) дана в табл. K1 (для рис. K1.0–K1.2 - в столбце 2, для рис. K1.3–K1.6 - в столбце 3, для рис. K1.7–K1.9 - в столбце 4).

Указания. Задача K1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения.

 

 

 

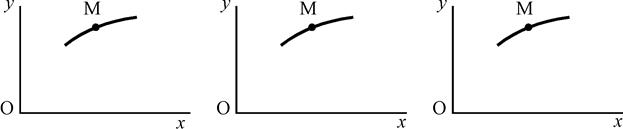
Рис. К1.0 Рис. К1.1 Рис. К1.2

 

 

 

Рис. К1.3 Рис. К1.4 Рис. К1.5

 

 

 

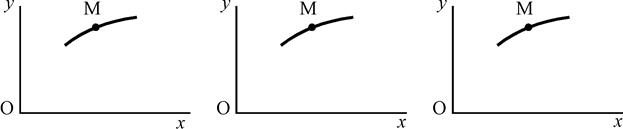
Рис. К1.6 Рис. К1.7 Рис. К1.8

 

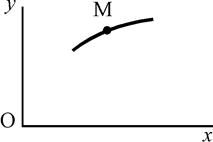
Рис. К1.9

Таблица K1

Номер условия	у = f 2 (t)
Рис. K1.0–K1.2	Рис. K1.3–K1.6	Рис. K1.7–K1.9

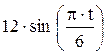
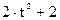
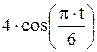
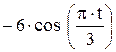
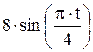
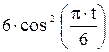
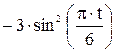
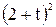
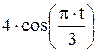
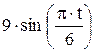
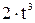
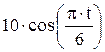
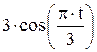
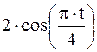
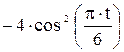
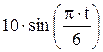
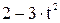
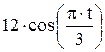
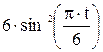
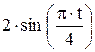
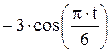
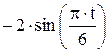
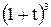
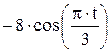
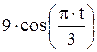
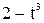
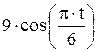
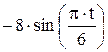
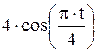
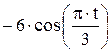
В задаче все искомые величины нужно определить только для момента времени t₁ = 1 с. В некоторых вариантах задачи при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы:

сos 2a = 1 – 2 sin² a = 2 cos² a – 1; sin 2a = 2×sin a×cos a.

Пример K1. Даны уравнения движения точки в плоскости ху:

x = 6×cos (p×t/6) – 3, y = – 4×cos² (p×t/6)

(х, у - в метрах, t - в секундах).

Определить уравнение траектории точки. Для момента времени t₁ = 1 с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Решение. Для определения траектории исключим из заданных уравнений движения время t, воспользовавшись подстановкой:

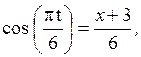
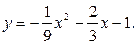
Из полученного выражения следует, что траекторией движения точки является парабола с нисходящими ветвями и осью, параллельной оси у; вершина параболы находится в точке с координатами х = -3 м, у = 0.

Найдем проекции вектора скорости на оси координат:

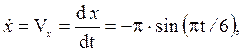
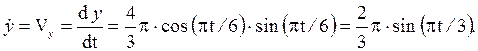
Подставив t₁ = 1 с в полученные выражения, находим

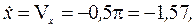
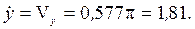
Скорость точки в момент времени t₁ = 1 с

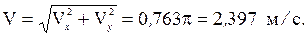
Найдем проекции вектора ускорения:

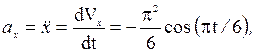
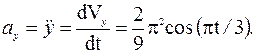
Для момента времени t₁ = 1 с

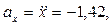
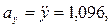
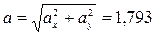м/с².

Касательное ускорение найдем по формуле

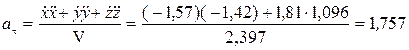м/с².

Нормальное ускорение

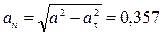м/с².

Вычислим радиус кривизны траектории в том месте, где находится точка в момент времени t₁ = 1 с:

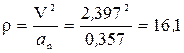м.

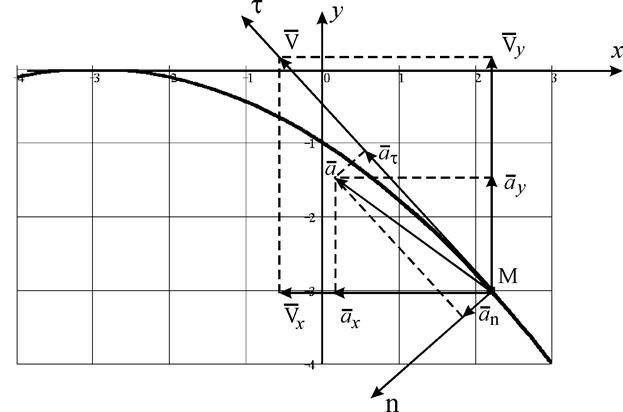
Рис. K1

Пользуясь уравнением траектории, вычерчиваем параболу (рис. K1) и показываем на ней точку М в заданный момент времени по ее координатам. Вектор скорости 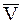строим по составляющим 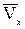и 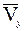; он должен быть направлен по касательной к траектории. Вектор ускорения 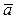находим по его составляющим 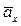и 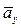. Далее найденный вектор раскладываем на направления касательной и нормали и получаем векторы касательного 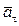и нормального 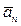ускорений. Полученные таким образом значения 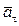и 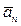должны совпасть с результатами их подсчета по формулам.

Вопросы для самоконтроля

1. Что называется траекторией точки?

2. Какие существуют способы задания движения и в чем заключается каждый из них?

3. Как при координатном способе задания движения точки определяется ее траектория?

4. Как найти проекции векторов скорости и ускорения точки на оси декартовой системы координат?

5. Как вычислить модули векторов скорости и ускорения точки по их проекциям на координатные оси?

6. Как определяются и что характеризуют нормальное и касательное ускорения точки?

7. Как найти радиус кривизны траектории в какой-либо ее точке?

Дата добавления: 2014-11-29