Кинематический расчет манипулятора

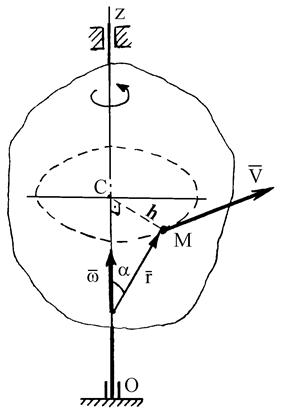
Рис. 30

Рассмотрим вращательное движение твердого тела вокруг неподвижной оси Оz (рис. 30). Выделим какую-либо точку М этого тела. Как известно [2], вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки, т. е.

(72)

Модуль скорости точки М равен модулю векторного произведения :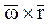

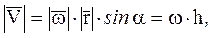
где h – расстояние от оси вращения до точки М.

Рассматривая вращение стержня ОА (рис. 31) вокруг оси, проходящей через точку О перпендикулярно к плоскости рисунка, и полагая, что вектор угловой скорости 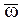направлен вдоль этой оси (к нам), применим формулу (72) для нахождения скорости точки А:

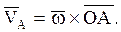(73)

Рис. 31

В формуле (73) стержень ОА представлен в виде вектора 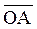. Направление этого вектора определим углом 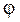, отсчитанным от положительного направления оси Ох против хода часовой стрелки. Отметим, что модуль вектора 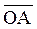равен длине стержня и, кроме того, вектор скорости 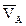перпендикулярен этому стержню. Угол между вектором 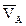и положительным направлением оси Оу также равен 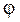, а модуль вектора 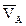равен

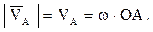
Проецируя векторное равенство (73) на координатные оси, получаем проекции 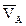на эти оси:

(74)

(75)

Формулы (74) и (75) будут справедливы для любых значений угла j, если отсчет этого угла производить против хода часовой стрелки от положительного направления оси Ох до направления вектора .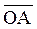

В случае плоскопараллельного (плоского) движения твердого тела скорость какой-либо точки В (рис. 32) равна геометрической сумме скорости точки А, принятой за полюс, и скорости точки В при вращении тела вокруг полюса А, т. е.

Рис. 32

(76)

где 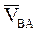определяется по формуле, аналогичной формуле (73):

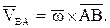
Дата добавления: 2014-11-29