
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поэтому


В момент времени t1 = 2 с имеем
s1 = AB1 = 20 cм, Vотн = 3 см/с, а отн = - 6 см/с2. (67)
Знаки показывают, что вектор 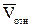 направлен в сторону положительного отсчета расстояния s, а вектор
направлен в сторону положительного отсчета расстояния s, а вектор 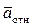 – в противоположную сторону. Изображаем эти векторы на рис. К3б.
– в противоположную сторону. Изображаем эти векторы на рис. К3б.
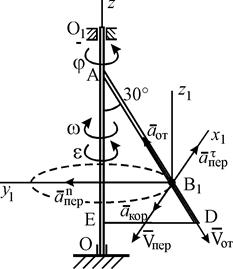
Рис. К3б
2. Переносное движение. Это движение (вращение) происходит по закону j = 0,1×t3 - 2,2t.
Найдем угловую скорость w и угловое ускорение e переносного вращения: w = 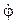 = 0,3t2 - 2,2; e =
= 0,3t2 - 2,2; e =  = 0,6t и при t1 = 2 с,
= 0,6t и при t1 = 2 с,
w = - 1 c-1, e = 1,2 c-2. (68)
Знаки указывают, что в момент t1 = 2 с направление e совпадает с направлением положительного отсчета угла j, а направление w ему противоположно; отметим это на рис. К3б соответствующими дуговыми стрелками.
Из рисунка находим расстояние h1 точки В1 от оси вращения z: h1 = AB1× sin 30° = 10 см. Тогда в момент t1 = 2 с, учитывая равенства (68), получаем:
Vпер = |w|×h1 = 10 cм/с,
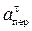 = |e|×h1 = 12 см/с2,
= |e|×h1 = 12 см/с2, 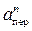 = w2×h1 = 10 см/с2. (69)
= w2×h1 = 10 см/с2. (69)
Изобразим на рис. К3б векторы  и
и 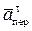 (с учетом знаков w и e)и
(с учетом знаков w и e)и  ; направлены векторы
; направлены векторы  и
и 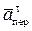 перпендикулярно плоскости ADE, а вектор
перпендикулярно плоскости ADE, а вектор  – по линии В1С к оси вращения.
– по линии В1С к оси вращения.
3. Кориолисово ускорение. Так как угол между вектором 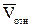 и осью вращения (вектором
и осью вращения (вектором 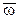 ) равен 30°, то численно в момент времени t1 = 2с
) равен 30°, то численно в момент времени t1 = 2с
а кор = 2×|Vотн| × |w| × sin 30° = 3 см/с2. (70)
Направление  найдем по правилу Н. Е. Жуковского. Для этого вектор
найдем по правилу Н. Е. Жуковского. Для этого вектор 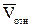 спроецируем на плоскость, перпендикулярную оси вращения (проекция направлена противоположно вектору
спроецируем на плоскость, перпендикулярную оси вращения (проекция направлена противоположно вектору  ) и затем эту проекцию повернем на 90° в сторону w, т. е. по ходу часовой стрелки; получим направление вектора
) и затем эту проекцию повернем на 90° в сторону w, т. е. по ходу часовой стрелки; получим направление вектора  . Он направлен перпендикулярно плоскости пластины так же, как вектор
. Он направлен перпендикулярно плоскости пластины так же, как вектор  (см. рис. К3б).
(см. рис. К3б).
4. Определение Vабс. Так как  =
=  +
+ 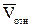 , а векторы
, а векторы  и
и 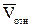 взаимно перпендикулярны, то
взаимно перпендикулярны, то  ; в момент времени t1 = 2 с Vабс = 10,44 см/с.
; в момент времени t1 = 2 с Vабс = 10,44 см/с.
5. Определение а абс. По теореме о сложении ускорений
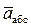 =
=  +
+ 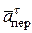 +
+ 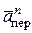 +
+  . (71)
. (71)
Для определения а абс проведем координатные оси В1хуz1 и вычислим проекции 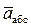 на эти оси. Учтем при этом, что векторы
на эти оси. Учтем при этом, что векторы 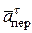 и
и  лежат на оси х 1, а векторы
лежат на оси х 1, а векторы 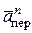 и
и  расположены в плоскости В 1 хуz 1, т. е. в плоскости пластины. Тогда, проецируя обе части равенства (71) на оси В1хуz1 и учтя одновременно равенства (67), (69), (70), получаем для момента времени t1 = 2 с:
расположены в плоскости В 1 хуz 1, т. е. в плоскости пластины. Тогда, проецируя обе части равенства (71) на оси В1хуz1 и учтя одновременно равенства (67), (69), (70), получаем для момента времени t1 = 2 с:
а абс х = | 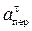 | – а кор = 9 см/с2,
| – а кор = 9 см/с2,
а абс у = 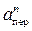 + | а отн|×sin 30 ° = 13 см/с2,
+ | а отн|×sin 30 ° = 13 см/с2,
а абс z = | а отн|×cos 30 ° = 5,20 см/с2.
Отсюда находим значение а абс:
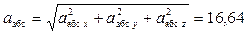 см/с2.
см/с2.
Ответ: Vабс = 10,44 см/с, а абс = 16,64 см/с2.
Вопросы для самоконтроля
1. Что понимается под составным (сложным) движением точки?
2. Что называется абсолютным, переносным и относительным движением точки?
3. Сформулируйте, что такое переносная скорость и переносное ускорение точки.
4. В чем заключается теорема об абсолютной скорости точки, совершающей составное движение.
5. Сформулируйте теорему об ускорениях точки в составном движении.
6. Как определить модуль и направление кориолисова ускорения точки?
7. В каких случаях ускорение Кориолиса равно нулю?
|
|
Дата добавления: 2014-11-29; Просмотров: 649; Нарушение авторских прав?; Мы поможем в написании вашей работы!